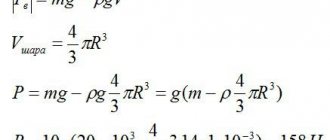Body density - relationship between mass and volume
For example, an iron cube with an edge of 10 cm has a mass of 7.8 kg, an aluminum cube of the same dimensions has a mass of 2.7 kg, and the mass of the same ice cube is 0.9 kg. The quantity characterizing the mass per unit volume of a given substance is called density. Density is equal to the quotient of the mass of the body and its volume, i.e.
ρ = m/V, where ρ (read “ro”) is the density of the body, m is its mass, V is the volume.
In the International System of Units SI, density is measured in kilograms per cubic meter (kg/m3); non-systemic units such as grams per cubic centimeter (g/cm3) are also often used. Obviously, 1 kg/m3 = 0.001 g/cm3. Note that when substances are heated, their density decreases or (more rarely) increases, but this change is so insignificant that it is neglected in calculations.
Let us make a reservation that the density of gases is not constant; When we talk about the density of a gas, we usually mean its density at 0 degrees Celsius and normal atmospheric pressure (760 millimeters of mercury).
§ 2 Problem solving What is the mass of sunflower oil in a 3 liter bottle if the oil density is 930 kg/m3?
Let's write down the condition of the problem. We know the volume of the bottle (denoted by the letter V) is 3 liters, and the density of sunflower oil (denoted by the letter ρ) is 930 kg/m3. Let's express the volume of the bottle in the International System of Units. 1 L = 0.001 m3, therefore 3 L is 0.003 m3.
Solution: To find the mass of a body, you need to multiply the density by the volume: m = ρ · V. Let's substitute the numerical values of the quantities: 930 kg/m3 · 0.003 m3 = 2.79 kg.
How many pieces of building bricks measuring 250 mm x 120 mm x 65 mm are allowed to be transported on a vehicle with a carrying capacity of 4 tons? Brick density is 1800 kg/m3.
Let's write down the condition of the problem and express the data in the International System of Units. The dimensions of the brick are known: length a = 250 mm = 0.25 m, width b = 120 mm = 0.12 m, height c = 60 mm = 0.06 m, brick density ρ = 1800 kg/m3, load capacity - maximum weight load that a car can transport – m = 4 t = 4000 kg. Find the number of bricks - denote by the Latin letter N.
Solution: The number of bricks can be found by dividing the total mass of all bricks by the mass of one brick: N = m/m1. To find the mass of one brick, you need to multiply the density by its volume: m1 = ρ · V. The brick has the shape of a rectangular parallelepiped, therefore, its volume is equal to the product of the length, width and height of the brick. Let's substitute the numerical values of known quantities and calculate. The volume of the brick is 0.0018 m3. The mass of one brick m1 is equal to 1800 kg/m3, multiplied by 0.0018 m3, equal to 3.24 kg. Then the number of bricks is N 4000 kg, divide by 3.24 kg and get 1234, 567 pieces or the number of whole bricks 1234 pieces.
The copper ball has a mass of 840 g and a volume of 120 cm3. Is this ball solid or hollow? Copper density is 8900 kg/m3.
Let's write down the condition of the problem. The known mass of the ball is m 840 g, which in the SI system is 0.84 kg, the volume of the ball is V = 120 cm3, in the SI system it is 0.00 012 m3, the density of copper is ρ = 8900 kg/m3. Determine whether the ball is solid or contains empty space inside?
Solution. Let's imagine that there are two copper balls lying on a lever scale, one is solid, the second contains empty space inside, that is, a hollow ball. If their masses are the same, then the volume of a hollow ball should be greater than the volume of a solid ball (Figure 1).
Let us determine the volume of a sphere consisting entirely of copper. If the volume turns out to be equal to 120 cm3, then the ball is solid and does not contain voids. If the calculated volume is less than 120 cm3, then there is a cavity inside.
To find the volume of a solid copper ball, divide the mass of the ball by its density. To simplify, we will carry out calculations in grams and cubic centimeters.
Calculation of body mass and volume
In everyday life, we often encounter the need to calculate the masses and volumes of different bodies. This can be conveniently done using density.
The densities of different substances are determined from tables, for example, the density of water is 1000 kg/m3, the density of ethyl alcohol is 800 kg/m3.
From the definition of density it follows that the mass of a body is equal to the product of its density and volume. The volume of a body is equal to the quotient of mass and density. This is used in calculations:
m = ρ * V; or V = m/p;
gdn m is the mass of a given body, ρ is its density, V is the volume of the body.
Calculation of body weight by its density
Knowing the density of substances is very important for many practical purposes. For engineers and builders, for example, knowledge of density is of enormous importance - this is how they can calculate the mass of a future mechanism or structure.
Density is determined by the formula $\rho = \frac{m}{V}$. Let's express the mass from here:
$$m = \rho V$$
To calculate the mass of a body, if its volume and density are known, you need to multiply the density by the volume.
Let's look at an example of a mass calculation problem. Calculate the mass of a part made of brass with a volume of $0.15 m^3$.
From Table 1 of the previous paragraph we take the value of the density of brass. It is equal to $8500 \frac{kg}{m^3}$.
Given: $\rho = 8500 \frac{kg}{m^3}$ $V = 0.15 m^3$
Find: $m -?$
Show solution and answer
Hide
Solution: $m = \rho \cdot V$ $m = 8500 \frac{kg}{m^3} \cdot 0.15 m^3 = 1275 kg \approx 1.3 t$
Answer: $m = 1275 kg \approx 1.3 t$.
Let's consider a more complex calculation example
An ingot of two metals with densities ρ1 and ρ2, has a mass m and a volume V. Determine the volume of these metals in the ingot.
Solution. Let V1 be the volume of the first metal, V2 be the volume of the second metal. Then V1 + V2 = V; V1 = V V2; ρ1V1 + p2V2 = ρ1V1 + ρ2 (V V1) = m
Solving this equation for V1, we get:
V1= (m ρ2V)/(ρ1 ρ2)
Now let's find V2:
V2= V — (m ρ2V)/(ρ1 ρ2)
Answer: the volume of the first body is equal to (m ρ2V)/(ρ1 ρ2), the second V is (m ρ2V)/(ρ1 ρ2). Note, however, that for ρ1 = ρ2 the problem does not have a unique solution.
Determination of density
Density is described as the amount of mass present in a substance for a given volume.
This is the main characteristic of matter, which explains the relationship between mass and volume (space occupied). It determines how tightly the molecules of an object are packed into a given amount of space.
The density of an object remains the same regardless of its shape and size.
Although, this can be changed if temperature and pressure are applied to an object, but a change in density also results in a change in matter.
The reason most objects sink or float is their density, as less dense objects tend to float while higher density objects tend to fall.
Why and who needs to know these formulas
Every country has standards by which products are manufactured. It doesn’t matter what industry it is - food, chemical or other. Standards can also be global. So, in order for the products produced at factories to meet these standards, knowledge about density, mass and volume is needed.
But why would anyone adhere to someone else's rules? To begin with, these rules were not pulled out of thin air. Various businessmen from all over the world came to this and found the optimal solution that satisfies both manufacturers and end users of the product. If everyone produced products as they pleased, it would be very difficult for people to choose a manufacturer. After all, even now, with all the standards and GOSTs, the choice is simply huge.
In addition, by ignoring physics and mathematics , you can develop products at a loss or make products that will not live up to expectations and will not look the way the manufacturer intended. There are other situations where knowledge of this kind is needed - when calculating the planned volume that products will occupy in a warehouse; weight of products that will need to be transferred, etc.
This knowledge may be required by engineers, technologists, designers and other professions whose activities are related to physical materials. Of course, this knowledge may not be useful for the average person. However, it is worth remembering the incident with Archimedes and then you will understand that knowledge is protection from deception and real power!
How can you find the mass of a substance?
Conversely, the mass of a substance is determined as the product of the molar mass and the amount of substance: m = n. M. Thus, the mass of 0.1 mol of Na is 0.1 mol × 23 g/mol = 2.3 g. The molar mass numerically always coincides with the molecular mass (or atomic mass - if the substance consists not of molecules, but of atoms) .
Interesting materials:
Do I need to register the engine when replacing it? Do you need a backup on your iPhone? Do I need to putty on smooth concrete walls? Do neighbors need consent to install a camera? Do I need to put double parentheses? Should I put a comma before including? Should I put a comma after there? Should I put a comma after only? Do I need to study for category BE? Do I need to notify the employment center about employment?
Weight of solid part
Home > Mass calculations > Solid part mass
05/09/2013 // Vladimir Trunov
This strange title of the article is explained only by the fact that parts of the same shape can be either solid or hollow (i.e. the next article will be called “Mass of a hollow part”).
Here is the time to remember that the mass of a body is its volume, multiplied by the density of its material (see density tables): The volume of a solid part is... its volume and nothing more.
Note : In the formulas below, all dimensions are measured in millimeters, and density is measured in grams per cubic centimeter. The letter indicates the ratio of the circumference of a circle to its diameter, which is approximately 3.14 .
Let's look at several simple forms (more complex ones, as you remember, can be made by adding or subtracting simple ones).
Mass of a parallelepiped (bar)
Volume of a parallelepiped: , where is the length, is the width, is the height. Then the mass:
Cylinder weight
Volume of the cylinder: , where is the diameter of the base, is the height of the cylinder. Then the mass:
Ball mass
Volume of the ball: , where is the diameter of the ball. Then the mass:
Ball segment mass
Volume of a ball segment: , where is the diameter of the base of the segment, and is the height of the segment. Then the mass:
Cone mass
The volume of any cone: , where is the area of the base, and is the height of the cone. For a round cone: , where is the diameter of the base, and is the height of the cone. Mass of round cone:
Mass of a truncated cone
Since it is impossible to embrace the immensity, we will consider only a round truncated cone. Its volume is the difference between the volumes of two nested cones: with bases and : , where , . After algebraic transformations that are not interesting to anyone, we get: , where is the diameter of the larger base, is the diameter of the smaller base, is the height of the truncated cone. Hence the mass:
Mass of the pyramid
The volume of any pyramid is equal to one third of the product of the area of its base and its height (the same as for cones (we often don’t notice how favorable the universe is to us)): , where is the area of the base and is the height of the pyramid. For a pyramid with a rectangular base: , where is the width, is the length, is the height of the pyramid. Then the mass of the pyramid is:
Mass of a truncated pyramid
Consider a truncated pyramid with a rectangular base. Its volume is the difference between the volumes of two similar pyramids with bases and: , where , . Having crossed out half of the notebook sheet, we get: , where , is the width and length of the larger base, , is the width and length of the smaller base, and is the height of the pyramid. And, leaving the remaining half of the sheet alone, based on symmetry considerations alone, we can write another formula, which differs from the previous one only by replacing W with L and vice versa. What is the difference between length and width? Only that we called them that. Let's call it the other way around and get: . Then the mass of a truncated rectangular pyramid is:
or
For a pyramid with a square base (, ), the formula looks simpler:
mass calculation
Weight of hollow part
Weight of wire, rod, rolled stock
Plate weight
Related Posts
How to use the density calculator:
Follow these instructions to calculate using this online tool. With this calculator you can perform calculations in simple and advanced modes. Let's take a look!
Inputs:
- First of all, select in the tab what you need to find.
- Then enter values in all designated fields according to the selected option.
- Finally, click the “Calculate” button.
Outputs:
Once you fill in all the fields, the calculator will show:
- Object Density
- Object mass
- Object volume
- Cube root of volume
The note:
There is an additional field where you can enter the material category and the name of the material, this calculator will find the density of the selected material. If you don't know the volume value, use the preview version of this calculator to calculate the volume, otherwise use the easy mode.
Experienced confirmation
Consider the experiment presented in Figure 1.
Figure 1. Weighing two identical bodies consisting of different substances.
Let's take two identical cylinders: they have the same shape and volume, but are made of different materials.
One is made of aluminum and the other is made of lead. Let's place them on different scales.
As a result, we will see that the mass of an aluminum cylinder will be almost 4 times less than the mass of a lead cylinder.
Bodies that have equal volumes, but consist of different substances, have different masses.
The figure shows 3 bodies weighing 100 g: ice, iron and gold.
Figure 2. Bodies of the same mass, but consisting of different substances.
Here are bodies of the same mass, but look at their volume. The volume of ice will be almost 8.5 times greater than the volume of a piece of iron of the same mass. And the volume of gold will be almost 3 times less than the volume of iron.
Bodies with equal masses, but consisting of different substances, have different volumes.
Densities of various gases
| Gas | $\rho, \frac{kg}{m^3}$ | $\rho, \frac{g}{cm^3}$ | Gas | $\rho, \frac{kg}{m^3}$ | $\rho, \frac{g}{cm^3}$ |
| Chlorine | 3,210 | 0,00321 | Carbon monoxide | 1,250 | 0,00125 |
| Carbon dioxide | 1,980 | 0,00198 | Natural gas | 0,800 | 0,0008 |
| Oxygen | 1,430 | 0,00143 | Water vapor (at $100^{\circ}$) | 0,590 | 0,00059 |
| Air (at $0^{\circ}C$ | 1,290 | 0,00129 | Helium | 0,180 | 0,00018 |
| Nitrogen | 1,250 | 0,00125 | Hydrogen | 0,090 | 0,00009 |
Table 3
Densities of various solids
| Solid | $\rho, \frac{kg}{m^3}$ | $\rho, \frac{g}{cm^3}$ | Solid | $\rho, \frac{kg}{m^3}$ | $\rho, \frac{g}{cm^3}$ |
| Osmium | 22 600 | 22,6 | Marble | 2700 | 2,7 |
| Iridium | 22 400 | 22,4 | Glass | 2500 | 2,5 |
| Platinum | 21 500 | 21,5 | Porcelain | 2300 | 2,3 |
| Gold | 19 300 | 19,3 | Concrete | 2300 | 2,3 |
| Lead | 11 300 | 11,3 | Brick | 1800 | 1,8 |
| Silver | 10 500 | 10,5 | Sugar | 1600 | 1,6 |
| Copper | 8900 | 8,9 | Plexiglas | 1200 | 1,2 |
| Brass | 8500 | 8,5 | Capron | 1100 | 1,1 |
| Steel, iron | 7800 | 7,8 | Polyethylene | 920 | 0,92 |
| Tin | 7300 | 7,3 | Paraffin | 900 | 0,90 |
| Zinc | 7100 | 7,1 | Ice | 900 | 0,90 |
| Cast iron | 7000 | 7,0 | Dry oak | 700 | 0,70 |
| Corundum | 4000 | 4,0 | Dry pine | 400 | 0,40 |
| Aluminum | 2700 | 2,7 | Cork | 240 | 0,24 |
Table 1
Densities of various liquids
| Liquid | $\rho, \frac{kg}{m^3}$ | $\rho, \frac{g}{cm^3}$ | Liquid | $\rho, \frac{kg}{m^3}$ | $\rho, \frac{g}{cm^3}$ |
| Mercury | 13 600 | 13,60 | Kerosene | 800 | 0,80 |
| Sulfuric acid | 1800 | 1,80 | Alcohol | 800 | 0,80 |
| Honey | 1350 | 1,35 | Oil | 800 | 0,80 |
| Sea water | 1030 | 1,03 | Acetone | 790 | 0,79 |
| Whole milk | 1030 | 1,03 | Ether | 710 | 0,41 |
| The water is clean | 1000 | 1,00 | Petrol | 710 | 0,71 |
| Sunflower oil | 930 | 0,93 | Liquid Tin (at $400^{\circ}$) | 6800 | 6,80 |
| Machine oil | 900 | 0,90 | Liquid air (at $-194^{\circ}$) | 860 | 0,86 |
table 2