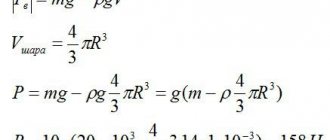How to calculate the weight of a metal barrel?
The calculation is made as follows: based on the specific gravity
steel or metal, as well as the dimensions of the rolled product (width, thickness, diameter, wall thickness, etc.),
the weight of
1 mm of the length of the rolled product is calculated and multiplied by the length of the rolled product - if
the weight
based on the length.
Interesting materials:
How much oil does a mower need per liter of gasoline? How much space do you need for PUBG Mobile? How much meat do you need for 1 kg of minced meat? How much milk do you need for 200 ml cappuccino? How long should you wear a cast for a broken arm? How many grades do you need to give for half a year? How many grades do you need for school certification? How much memory do you need to backup your iPhone? How much memory does an iPhone need? How much yeast do you need to put in the dough?
What is a cylinder?
Before moving on to the answer to the question of what the mass of a cylinder and its volume are, it is worth considering what this spatial figure represents. It should immediately be noted that a cylinder is a three-dimensional object. That is, in space you can measure three of its parameters along each of the axes in the Cartesian rectangular coordinate system. In fact, to unambiguously determine the dimensions of a cylinder, it is enough to know only two of its parameters.
How to calculate the mass of a rectangular profile?
A rectangular profile is a parallelepiped with a given wall thickness. The wall thickness is specified in the technical documentation for a specific sample.
Mass calculation can be done in two ways. In the first method, the cross-sectional area is calculated: for a sheet of a given thickness. Calculate the mass of a rectangular parallelepiped based on its external dimensions. Then the same calculations are made for a parallelepiped with internal dimensions. The difference between the two values will be the desired characteristic.
Read also: DIY shooting bag
In the second method, the weight of one wall of the structure is calculated. If the cross-section is square, multiply by four. If it is rectangular, the sizes of the smaller and larger walls will be calculated separately. Then multiply each value by two and add the results to get the final figure.
Square profile weight
To simplify the process, special tables have been developed.
Gross and net weight - what is it?
If you take a closer look at the inscriptions on product packaging, you can find, among other characteristics, such as “net weight”, which is contained, for example, on any food product. What is missing from this mass?
“ Gross ” and “ net ” - these two economic terms came to us from the Italian language. Literally ' brutto ' is translated as “bad”, while ‘ netto ’ is “clean”, in other words, cleared of excess. If we study the etymology of these words even deeper, we can find their origin in Latin, where, for example, 'brutus' means "stupid, foolish, rude." Interestingly, the Italians themselves use the definitions “net” and “lordo” (“lordo” – dirty, containing impurities) to name the two types of mass.
Net weight is the name given to the weight of the product itself, the product, without taking into account the weight of its packaging (be it a box, candy wrapper or other container). The term “net” is also used to refer to the net price of a product minus discounts and allowances. So, for the buyer, the net price is the amount of money actually paid for the product, while for the seller it is the net profit from the sale of the product, minus all costs and expenses.
Gross weight is the opposite of net weight, that is, the total weight of the product, including the container in which it is packaged. The opposite of the term “net,” “gross” is used to denote the price without deductions (for example, the price on the stock market) or profit without deductions of costs.
Semi-net weight is considered to be the weight of the product together with the primary packaging (packaging that cannot be separated from the product before its use without compromising the consumer properties of the product). Examples of such goods are a can of canned food, a tube of toothpaste, and a bottle of perfume.
Often on the packaging, but this is wrong. Mass and weight are different concepts, although their numerical values are almost the same. Mass is something material (piece, body, etc.) measured in kg. Weight is the force with which a mass is attracted to the ground. Measured in N (newton). So you need to indicate “Net weight” on the label.
What makes calculating the weight of metal more difficult?
A serious difference in the data obtained for calculating the mass of a steel product is the technology of its production. The difference between cold-rolled metal and hot-rolled metal can be quite significant. We are talking about the accuracy of geometric characteristics while maintaining density along the entire length of the product.
The use of continuous heating and subsequent cooling leads to such negative phenomena as oxidation and recrystallization. The unevenness of these processes causes a change in such a parameter as thickness.
The accuracy of calculations for cold-rolled and hot-rolled metal profiles will differ. The error caused by thickness instability requires obtaining some average value.
How to find out the mass of a hexagonal profile?
Solid metal rods with a hexagonal cross-section are often used. The calculation method for such products remains the same. It is necessary to remember from the school geometry course how the volume of a regular hexagonal parallelepiped is calculated.
The task is greatly simplified if you know the size or number of such a rental. All numbers are given in a standardized table.
The hexagonal profile with the smallest number 10 weighs only 0.68 kg, the largest number 60 weighs 24.5 kg.
The calculations are based on a formula for calculating the volume of a regular hexagonal prism. Having calculated this volume, it is multiplied by the density of the metal. A mass of hexagonal product is obtained.
It should be remembered that the use of simplified methods gives approximate results. They are used for express assessments. When developing design documentation in detail, more accurate indicators are used.
We calculate the weight of rolled sheets
Calculating the weight of rolled metal is a fairly simple task of this class. Simplicity is determined by the shape of the sample being studied. To begin calculations, you need to know the following characteristics:
- geometric dimensions of the test sample;
- metal density (for steel you can use the average indicator, which is equal to 7850 kg/m 3);
For example, the weight of a sheet whose size is one meter long, two meters wide, 0.35 mm thick will weigh 5.5 kg. A sheet 5 mm thick, measuring 1.5 m wide and 6 meters long will weigh 353.25 kg.
Before using a metal sheet as a ceiling or building structure, you should evaluate its weight.
Sheet weight
Selection of method and method for manufacturing the workpiece:
It is advisable to obtain the initial workpiece by casting.
We will select the casting manufacturing method based on technological capabilities for various casting methods:
The batch of blanks specified in the condition is N=”5″ pcs/year. Sand casting has no minimum batch size restrictions. For other casting methods, the minimum batch is 200 pieces/year or more. Other requirements for sand casting:
Casting material: cast iron – meets the requirements.
Read also: Chainsaw chain stops when loaded
Casting weight: 29.5 kg.
The minimum wall thickness is 27 mm, which is more than 3 mm - the condition is met.
Maximum overall size 288mm.
The dimensional accuracy class, the roughness of unprocessed surfaces and the casting complexity group are not regulated.
When casting in sand molds, the production of a part weighing m=”29.5″ kg in the amount of 5 pieces per year refers to a single production. In single production conditions, castings are made by casting into sand molds, made by hand using wooden models.
Calculation of the mass of a hollow cylinder
It is interesting to calculate how much mass a copper cylinder will have if it is empty inside. For example, let it be made of a thin copper sheet with a thickness of only d = 2 mm.
To solve this problem, you need to find the volume of the copper itself from which the object is made. Not the volume of the cylinder. Since the thickness of the sheet is small compared to the dimensions of the cylinder (d = 2 mm and r = 10 cm), then the volume of copper from which the object is made can be found by multiplying the entire surface area of the cylinder by the thickness of the copper sheet, we obtain: V = d *S3 = d*2*pi*r*(r+h). Substituting the data from the previous problem, we get: V = 0.2*2*3.14*10*(10+10) = 251.2 cm 3. The mass of a hollow cylinder can be obtained by multiplying the resulting volume of copper required for its manufacture by the density of copper: m = 251.2 * 8.96 = 2251 g or 2.3 kg. That is, the considered hollow cylinder weighs 12 (28.1/2.3) times less than a homogeneous one.
Source
Homogeneous and hollow cylinders
From the result obtained above, it can be seen that a copper cylinder with relatively small dimensions (10 cm) has a large mass (28 kg). This is due not only to the fact that it is made of heavy material, but also to the fact that it is homogeneous. This fact is important to understand, since the above formula for calculating mass can only be used if the cylinder is completely (outside and inside) composed of the same material, that is, it is homogeneous.
In practice, hollow cylinders are often used (for example, cylindrical water barrels). That is, they are made of thin sheets of some material, but are empty inside. For a hollow cylinder, the specified formula for calculating mass cannot be used.
Cylinder weight formula calculator
On this page the calculator will help you calculate the volume of a cylinder online. To calculate, specify the height, radius or area of the base. Calculations are made in millimeters, centimeters, meters. The result is displayed in cubic centimeters, liters and cubic meters.
A cylinder is a geometric body bounded by a cylindrical surface and two parallel planes intersecting it.
By height and radius
Formula for the volume of a cylinder using height and radius:
V = π r² h
Through base area and height
Formula for the volume of a cylinder in terms of height and base area:
Using our Online calculator for calculating the volume of a cylinder, you can quickly and accurately calculate the volume of a cylinder. In order to calculate the volume of a cylinder, first select the formula by which you are going to make the calculation. The volume of a cylinder (depending on the initial data) can be calculated in two ways: 1. through the height and radius of the base; 2. through the height and area of the base. Then enter the values of the initial data for calculation (the height of the cylinder, the value of the radius of the base of the cylinder (or the value of the area of the base of the cylinder) and click the “Calculate” button. You can also specify the accuracy of the result obtained, i.e. the number of decimal places to which it will be The calculated volume of the cylinder has been rounded.
Determination of cylinder mass
Finally, it’s worth going directly to the topic of the article. How to determine the mass of a cylinder? To do this, you need to know its volume, the formula for calculating which was presented above. And the density of the substance of which it consists. Mass is determined by a simple formula: m = ρ*V, where ρ is the density of the material forming the object in question.
The concept of density characterizes the mass of a substance that is located in a unit volume of space. For example. It is known that iron has a higher density than wood. This means that in the case of equal volumes of iron and wood, the former will have a much greater mass than the latter (approximately 16 times).
Volume and surface area
As can be seen from the above, a cylinder is determined by two parameters: the height h and the radius of its base r. Knowing these parameters, it is possible to calculate all other characteristics of the body in question. Below are the main ones:
- Base area. This value is calculated by the formula: S1 = 2*pi*r 2, where pi is the number pi equal to 3.14. The number 2 in the formula appears because the cylinder has two identical bases.
- The area of a cylindrical surface. It can be calculated as follows: S2 = 2*pi*r*h. It is simple to understand this formula: if a cylindrical surface is cut vertically from one base to another and unfolded, you will get a rectangle, the height of which will be equal to the height of the cylinder, and the width will correspond to the circumference of the base of the volumetric figure. Since the area of the resulting rectangle is the product of its sides, which are equal to h and 2*pi*r, the formula presented above is obtained.
- Surface area of a cylinder. It is equal to the sum of the areas S1 and S2, we get: S3 = S1 + S2 = 2*pi*r 2 + 2*pi*r*h = 2*pi*r*(r+h).
- Volume. This value is easy to find; you just need to multiply the area of one base by the height of the figure: V = (S1/2)*h = pi*r 2 *h.
Determining the WEIGHT of a part from its drawing
The mass of the part is determined
where V
– volume of the part, r – density of the material from which the part is made.
Thus, to determine the mass of a part, it is necessary to determine the volume of the part. To do this, we divide the part into shapes, for which the volume of the part can be determined using known formulas (Table 2.1)
| Name | Visual representation | Sketch | Volume |
| Cylinder | |||
| Prism | V = abc | ||
| Pyramid | base area |
| Hollow cylinder |
| Obliquely cut cylinder |
| Ball |
| Ball sector |
| Ball segment |
| Cone | |
| Truncated pyramid | , where f 1 and f 2 are the areas of the bases of the pyramid |
| Frustum | |
| Barrel | |
| Body of rotation | Volume V of a body of revolution formed by the rotation of area F , multiplied by the path described by its center of gravity S around an axis of radius r V=2prF=2prab |
As an example, consider determining the volume of the shaft shown in Fig. 2.1. Let's divide the shaft into simple (from the point of view of calculating volume) bodies (Fig. 2.2) and calculate their volume.
1. Chamfer volume (1) – truncated cone (Fig. 2.2)
, . .
3. Groove volume (3) with cross section S
(Fig. 2.3,
a
) and 10 mm long for the prismatic part of the groove
a b
, .
Let's take into account the volume of the cylinder from the side half-cylinders of the groove. Let's accept
r =b/
2 = 2.5
mm
– cylinder radius,
h / = h
+ 0.5(
R —
) = 3 + 0.5(6 — ‑ height
cylinder equal to the depth of the groove and the top of the cylinder of the groove.
Then the volume of the cylindrical part of the keyway is:
The final volume of the keyway will be
4. Volume of fillet 4 with radius r = 1 mm
(Fig. 2.4).
The fillet area is determined as the difference between the areas of the square Sк = r 2
and quarter circle (sector)
Sc = pr 2 /
4 (Fig. 2.4)
Sg = r 2 - pr 2 /4 = r 2
(4- p)/
4=
1 2 (4-π)/4 = 0.22
mm
2
Rice. 2.4
Center of gravity along the X
square
xK
=
, and a quarter of a circle is a sector of a circle with an angle of 90º ,
Center of gravity of the fillet along the X
:
Segment area
seg. will be determined as the difference between the area of the sector with angle α and the area of the triangle
Finding the numerical value of the flat's volume
. ,
where S=
p 2 tg60 o /4,
L =
2πr
–
thread length,
n
=
l/p
– number of turns,
l
– thread length.
How to find out the mass of a pipe
To determine the mass of pipes, it is optimal to use tables.
Read also: Silver plating at home
| Nominal diameter, inch/mm | Wall thickness, mm | Weight, kg | Nominal diameter, inch/mm | Wall thickness, mm | Weight, kg |
| 1/4 (8) | 2,35 | 0,65 | 1 1/4 (32) | 3,25 | 3,14 |
| 1/2 (15) | 2,65 | 1,22 | 1 1/2 (40) | 3,25 | 3,61 |
| 3/4 (20) | 2,65 | 1,58 | 2 (50) | 3,65 | 5,1 |
| 1 (25) | 3,25 | 2,44 | 2 1/2 (65) | 3,65 | 6,51 |
If you don’t have access to reference materials, and simple geometric formulas are not an obstacle for you, calculate the weight yourself. To do this, we find the difference between the area of the circle along the outer radius and the area along the inner radius. We multiply the resulting difference by the length of the pipe and the density of the steel - 7,850 kg/m3.
For pipes made of non-ferrous metals, the conversion factors that we discussed above are used.
Calculation of the mass of a copper cylinder
Let's consider a simple problem. You need to find the mass of a cylinder made of copper. To be specific, let the cylinder have a diameter of 20 cm and a height of 10 cm.
Before you begin solving the problem, you should understand the initial data. The radius of the cylinder is equal to half its diameter, which means r = 20/2 = 10 cm, and the height is h = 10 cm. Since the cylinder considered in the problem is made of copper, then, referring to the reference data, we write down the density value of this material: ρ = 8 .96 g/cm 3 (for a temperature of 20 °C).
Now you can start solving the problem. First, let's calculate the volume: V = pi*r 2 *h = 3.14*(10) 2 *10 = 3140 cm 3 . Then the mass of the cylinder will be equal to: m = ρ*V = 8.96 * 3140 = 28134 grams or approximately 28 kilograms.