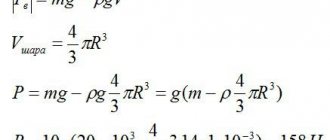Body mass:
According to Newton's first law, in inertial reference systems the speed of a body does not change, provided that the influence of other bodies is compensated. What if this condition is not met?
Let's conduct an experiment with an iron ball suspended on a thread attached to a stationary tripod. The ball is at rest because the action of the thread compensates for the Earth's gravity. If you bring a magnet to the side of the ball, then under its action the ball will begin to move (Fig. 29, a).
If you remove the magnet and cut the thread on which the ball is suspended, then the influence of the Earth will not be balanced, and, as you already know well, the ball will begin to move rapidly downward (Fig. 29. b).
These experiments and numerous observations of various bodies in the surrounding world allow us to conclude that the accelerated movement of a body is the result of the uncompensated influence of other bodies on it.
Is it possible to have any effect on a specific body without this body also exerting its action (reaction)?
If in our experiment with a ball we hang a magnet nearby on a thread, we will be able to observe the simultaneous movement of the ball and the magnet towards each other (Fig. 29, c).
When hitting the ball (Fig. 30), a person feels the impact of the ball during the impact. If you hold a heavy briefcase by the handle for some time, indentations will remain on your palm due to the action of this load on it.
To investigate how bodies interact and what their accelerations depend on, let’s conduct several experiments. Let's take two balls of the same size—one made of aluminum and the other made of iron—and consider their collision as they move along a stationary horizontal metal chute.
Let the iron ball roll along the chute towards the aluminum ball at rest (Fig. 31, a). We will see that during the interaction (collision) both balls will change their speed, that is, they will have acceleration (Fig. 31, b). If both balls are moving towards each other, then when they collide, their speeds also change (Fig. 32, a, b).
Rice. 31
Rice. 32
This means that during interaction both balls change their speed, but it is difficult to measure and compare the accelerations they receive upon impact in such an experiment. Therefore, we will conduct an experiment in which the accelerations of interacting bodies can be determined quite simply.
For the experiment, we use two identical-sized cylinders made of aluminum and copper with holes drilled along their axes. We insert a smooth rod into the holes of the cylinders, along which the cylinders can easily slide. Let us fix the rod with the cylinders in an installation that can rotate the rod at a constant angular velocity in the horizontal plane.
If the rod is rotated, then one can observe the sliding of the cylinders towards the ends of the rod (Fig. 33, a). Let's stop the rotation, tie the cylinders with a thread and put the rod into rotation again. Since the cylinders now interact with each other using a thread, they will rotate together with the rod, being at certain distances from the axis of rotation (Fig. 33, b). Let's calculate and compare the centripetal accelerations of the cylinders.
Rice. 33
Let the rod together with the cylinders rotate with angular velocity ω and the centers of the cylinders move along circles of radii R1 and R2, which are easy to measure (see Fig. 33, b). Then the accelerations of the cylinders according to the known kinematic formulas are equal: a1 =ω2R1; a2 = ω2R2.
Let's compare the cylinder acceleration modules:
Thus, the acceleration modules are related as the radii of the circles along which the centers of the cylinders rotate, and in our experience this ratio is 3.3.
If this experiment is carried out at a different angular velocity of rotation or by connecting the cylinders with a thread of a different length, then the radii of the circles will change, but their ratio, and therefore the ratio of the acceleration modules, will remain the same. How to explain the constancy of the ratios of acceleration modules for two interacting cylinders?
Acceleration characterizes the rate of change in the speed of a body. In the 7th grade, you became acquainted with a physical quantity - body mass, on which the magnitude of the change in the speed of the body also depended. You know that the greater the mass of a body, the more difficult it is to change its speed.
Let's compare the masses of copper and aluminum cylinders. Since their sizes are the same, the volumes are the same, and the mass ratio is equal to the ratio of the densities of copper and aluminum, i.e.:
Thus, a comparison of the ratios of the acceleration modules and the masses of the cylinders shows that the accelerations of the cylinders are inversely proportional to their masses:
Numerous experiments conducted by scientists to study a wide variety of interactions between bodies show that the pattern we obtained is always fulfilled.
The ratio of the acceleration modules of two interacting bodies is equal to the inverse ratio of their masses.
What is body weight? A complete answer to this question requires knowledge of more complex branches of physics.
Therefore, let's consider a simplified idea of body weight. In 8th grade you learned that all bodies are made of atoms and molecules that have mass. Then the mass of a body is the total mass of all its particles. Based on experimental data, the simplified concept of “mass” can be characterized as follows:
- body mass is a physical scalar quantity equal to the sum of the masses of all particles (or material points) of which it consists (additivity property);
- for a given system of bodies, the law of conservation of mass is satisfied - during any processes in the system, its mass remains unchanged;
- body mass does not depend either on the interactions in which the body participates or on the speed of the body;
- The mass of a body during its interaction with other bodies determines the magnitude of the acceleration received by the body.
You already know that the SI unit of mass is 1 kg. This is the mass of a specially made standard (sample). How to measure the mass of a certain body using a mass standard?
If you bring a standard and a body of unknown mass into interaction, and then measure their accelerations, you can determine the unknown mass of the body:
Of course, for ordinary bodies this method is less convenient than conventional weighing. But the determination of the masses of cosmic bodies, for example, planets by the acceleration of their satellites or the smallest particles of matter (atoms, molecules, etc.) by the acceleration during their interaction, is almost always done.
Main conclusions:
- A body moves accelerated in an inertial frame of reference if the influence of other bodies on it is not compensated.
- When two bodies interact, both bodies experience an impact, and the ratio of the acceleration modules of the two interacting bodies is equal to the inverse ratio of their masses.
- The mass of a body is a physical scalar additive quantity that does not depend on the interactions in which the body participates and on its speed.
Physics cheat sheets for 7th grade
It is difficult to cover the entire physics course in one article, but we covered the main topics for grade 7 and this is enough to refresh your memory. Download and print both cheat sheets - one of them (detailed) will be useful for thoughtful preparation for the Unified State Exam and Unified State Exam, and the second (short) will be used for solving problems.
.
.
For those who are homeschooled or are forced to study the material on their own due to absences due to illness, we also recommend a textbook on physics by A. V. Peryshkin with formulas for grade 7 and easy, accessible explanations on all topics. It was written several decades ago, but is still very popular and in demand.
Atomic and nuclear physics
To the table of contents...
The energy of a quantum of an electromagnetic wave (including light) or, in other words, the energy of a photon is calculated by the formula:
Photon momentum:
Einstein's formula for the external photoelectric effect (EPE):
The maximum kinetic energy of emitted electrons during the photoelectric effect can be expressed in terms of the value of the retarding voltage Uз and the elementary charge e:
There is a cutoff frequency or wavelength of light (called the red cutoff of the photoelectric effect) such that light with a lower frequency or longer wavelength cannot cause the photoelectric effect. These values are related to the work function value as follows:
Bohr's second postulate or frequency rule (FRR):
In the hydrogen atom, the following relationships are satisfied, connecting the radius of the trajectory of an electron rotating around the nucleus, its speed and energy in the first orbit with similar characteristics in the remaining orbits:
In any orbit in a hydrogen atom, the kinetic (K) and potential (P) energies of the electron are related to the total energy (E) by the following formulas:
The total number of nucleons in the nucleus is equal to the sum of the number of protons and neutrons:
Mass defect:
Nuclear binding energy expressed in SI units:
Nuclear binding energy expressed in MeV (where mass is taken in atomic units):
Alpha decay formula:
Beta decay formula:
Law of radioactive decay:
Nuclear reactions
For an arbitrary nuclear reaction described by a formula of the form:
The following conditions are met:
The energy yield of such a nuclear reaction is equal to:
Measurement of physical quantities
| By measuring is the determination, using tools and technical means, of the numerical value of a physical quantity. The measurement result is compared with a certain standard taken as a unit. As a result, the value of a physical quantity is considered to be the resulting number indicating the units of measurement. |
In the 7th grade physics course, they study the rules of measurement using instruments with a scale. If the scale division value is unknown, you can find it out using the following formula:
CD = (max − min) / n, where CD is the division price, max is the maximum scale value, min is the minimum scale value, n is the number of divisions between them.
Instead of the maximum and minimum, we can take any other scale values whose numerical expression is known to us.
There are direct and indirect measurements:
- with direct measurement, the result can be seen directly on the instrument scale;
- with indirect measurement, the value of a quantity is calculated through another quantity (for example, the average speed is determined based on several speed measurements).
For convenience and standardization of measurements, the International System of Units SI was adopted in 1963. It regulates which units of measurement are considered basic and used for formulas. The designations of these units are also taught in the 7th grade physics curriculum.
Oscillations
To the table of contents...
An equation describing physical systems capable of performing harmonic oscillations with a cyclic frequency ω0:
The solution to the previous equation is the equation of motion for harmonic vibrations and has the form:
The oscillation period is calculated by the formula:
Oscillation frequency:
Cyclic oscillation frequency:
The dependence of speed on time for harmonic mechanical vibrations is expressed by the following formula:
Maximum speed value for harmonic mechanical vibrations:
Dependence of acceleration on time for harmonic mechanical vibrations:
Maximum acceleration value for mechanical harmonic vibrations:
The cyclic frequency of oscillations of a mathematical pendulum is calculated by the formula:
Period of oscillation of a mathematical pendulum:
Cyclic frequency of oscillation of a spring pendulum:
Oscillation period of a spring pendulum:
The maximum value of kinetic energy during mechanical harmonic vibrations is given by the formula:
The maximum value of potential energy during mechanical harmonic oscillations of a spring pendulum:
The relationship between the energy characteristics of the mechanical oscillatory process:
Energy characteristics and their relationship during fluctuations in the electrical circuit:
The period of harmonic oscillations in an electric oscillatory circuit is determined by the formula:
Cyclic frequency of oscillations in an electric oscillatory circuit:
The dependence of the charge on a capacitor on time during oscillations in the electrical circuit is described by the law:
Dependence of the electric current flowing through an inductor on time during oscillations in the electrical circuit:
Dependence of the voltage on the capacitor on time during fluctuations in the electrical circuit:
The maximum current value for harmonic oscillations in an electrical circuit can be calculated using the formula:
The maximum voltage value on the capacitor during harmonic oscillations in the electrical circuit:
Alternating current is characterized by effective values of current and voltage, which are related to the amplitude values of the corresponding quantities as follows. Effective current value:
Effective voltage value:
AC power:
Transformer
If the voltage at the input to the transformer is U1, and at the output U2, and the number of turns in the primary winding is n1, and in the secondary winding n2, then the following relationship holds:
The transformation coefficient is calculated using the formula:
If the transformer is ideal, then the following relation holds (the input and output powers are equal):
In a non-ideal transformer, the concept of efficiency is introduced:
Waves
The wavelength can be calculated using the formula:
The difference in the phases of oscillations of two points of the wave, the distance between which is l:
The speed of an electromagnetic wave (including light) in a certain medium:
The speed of an electromagnetic wave (including light) in a vacuum is constant and equal to c = 3∙108 m/s, it can also be calculated using the formula:
The speeds of an electromagnetic wave (including light) in a medium and in a vacuum are also related by the formula:
In this case, the refractive index of a certain substance can be calculated using the formula:
Mechanical movement: formulas for grade 7
| Mechanical motion is the movement of a body in space, as a result of which it changes its position relative to other bodies. The patterns of such movement are studied within the framework of mechanics and specifically its section - kinematics. |
In order to describe motion, a reference body, a coordinate system, and an instrument for measuring time are required. These are the components of the reference system.
The study of mechanical motion in the 7th grade physics course includes the following terms:
- The displacement of a body is a vector drawn from the starting point to the ending point.
- The trajectory of movement is a mental line along which the body moves.
- Path is the length of the body’s trajectory from the start to the end point.
- Speed is the speed at which a body moves or the ratio of the distance it travels to the time it travels.
- Acceleration is the rate of change in speed at which a body moves.
| Uniform linear motion means that a body moves along a straight line at the same speed. In this case, the displacement of the body and its path will be equal. |
Formula for the speed of uniform rectilinear motion:
V = S / t, where S is the path of the body, t is the time during which this path is covered.
Formula for the speed of uniform curvilinear motion:
where S1 and S2 are sections of the path, and t1 and t2 are the time during which each of them was covered.
The SI unit of speed is meters per second (m/s).
Formula for speed of uniformly accelerated motion:
V = V0 + at, where V0 is the initial velocity and is the acceleration.
The SI unit of acceleration is m/s2.
Thermodynamics
To the table of contents...
The amount of heat (energy) required to heat a certain body (or the amount of heat released when the body cools) is calculated by the formula:
The heat capacity (C - large) of a body can be calculated through the specific heat capacity (c - small) of the substance and the mass of the body using the following formula:
Then the formula for the amount of heat necessary to heat the body, or released when the body cools, can be rewritten as follows:
Phase transformations. During vaporization it is absorbed and during condensation an amount of heat is released equal to:
During melting it is absorbed, and during crystallization an amount of heat is released equal to:
When fuel burns, an amount of heat is released equal to:
Heat balance equation (HBE). For a closed system of bodies, the following holds (the sum of heat given is equal to the sum of heat received):
If all heat is written taking into account the sign, where “+” corresponds to the receipt of energy by the body, and “–” to the release, then this equation can be written in the form:
Ideal gas work:
If the gas pressure changes, then the work done by the gas is calculated as the area of the figure under the graph in p–V coordinates. Internal energy of an ideal monatomic gas:
The change in internal energy is calculated using the formula:
First law (first law) of thermodynamics (FLE):
For various isoprocesses, formulas can be written by which the resulting heat Q, the change in internal energy ΔU and the gas work A can be calculated. Isochoric process (V = const):
Isobaric process (p = const):
Isothermal process (T = const):
Adiabatic process (Q = 0):
The efficiency of a heat engine can be calculated using the formula:
Where: Q1 is the amount of heat received by the working fluid in one cycle from the heater, Q2 is the amount of heat transferred by the working fluid to the refrigerator in one cycle. Work done by a heat engine in one cycle:
The highest efficiency at given temperatures of the heater T1 and refrigerator T2 is achieved if the heat engine operates according to the Carnot cycle. This Carnot cycle efficiency is equal to:
Absolute humidity is calculated as water vapor density (from the Clapeyron-Mendeleev equation the ratio of mass to volume is expressed and the following formula is obtained):
Relative air humidity can be calculated using the following formulas:
Potential energy of a liquid surface with area S:
The surface tension force acting on a section of the liquid boundary of length L:
Height of the liquid column in the capillary:
With complete wetting θ = 0°, cos θ = 1. In this case, the height of the liquid column in the capillary will be equal to:
With complete non-wetting, θ = 180°, cos θ = –1 and, therefore, h < 0. The level of the non-wetting liquid in the capillary drops below the level of the liquid in the vessel into which the capillary is lowered.
Gravity, weight, mass, density
Formulas, concepts and definitions that describe these physical characteristics are studied in 7th grade as part of a section of physics called dynamics.
| The weight of a body or substance is a vector quantity that characterizes the force with which it acts on a horizontal surface or vertical suspension. This quantity should not be confused with mass, which is a scalar quantity. |
Body weight is measured in newtons, body mass in grams and kilograms.
Weight formula:
P = mg, where m is the mass of the body, g is the acceleration of gravity.
The acceleration of free fall occurs under the influence of gravity, to which all bodies on our planet are subject.
g = 9.806 65 m/s2 or 9.8 N/kg
If a body is at rest or in linear uniform motion, its weight is equal to the force of gravity.
Fstrand = mg
But these concepts cannot be identified: the force of gravity acts on a body due to the presence of gravity, while weight is the force with which the body itself acts on the surface.
| The density of a body or substance is a value indicating how much mass a given substance has when occupying a unit volume. Density is directly proportional to mass and inversely proportional to volume. |
Density Formula:
ρ = m / V, where m is the mass of a body or substance, V is the occupied volume.
SI unit of density: kg/m3.
Online physics courses at Skysmart are no less exciting than our articles!
Quantity of substance
From the previous formulas it is clear that the molar mass and the amount of a substance are closely related. Let's look at this connection in more detail. Let's start with the fact that the amount of a substance can be denoted by either a Latin letter or a Greek letter (nu). The international designation is , but do not be surprised when you encounter any of these letters in formulas.
In the formula for finding the molar mass, we denoted the amount of substance through:
, hence .
Using this, we can find the amount of a substance (in moles) if we know its absolute and molar mass.
Example 1
How to determine what amount of substance is included in 350 g of barium sulfate BaSO4?
Let's use the formula.
We remember that M = Mr (the value of the molar mass is equal to the value of the relative molecular mass).
Mr(BaSO4) = Ar(Ba) + Ar(S) + Ar(O) 4 = 137 + 32 + 16 4 = 233.
M(BaSO4) = Mr(BaSO4) = 233 g/mol.
Let's substitute the molar mass value into the formula:
mole.
There is another formula for the amount of a substance that allows you to find it if the number of molecules or other structural units is known.
, where is the number of structural units, is Avogadro’s number.
Example 2
Let's say a certain volume of CaCO3 contains 3.01 · 1023 molecules. How to find the amount of a substance corresponding to a given volume?
Let's use the formula mole.
Mechanical lever, moment of force
Archimedes spoke about a mechanical lever when he promised to turn the Earth upside down if only a suitable fulcrum could be found. It is a simple mechanism that helps lift weights attached to one end by applying force to the other end. In this case, the weight of the load greatly exceeds the applied force. In grade 7, physical formulas describing this process are studied in the same section of dynamics.
| Lever arm - this is a kind of solid body capable of rotating around a fixed point of support, on one end of which a force is applied, and on the other there is a load. The perpendicular drawn from the fulcrum to the line of action of the force is called the arm of the force. |
A lever is in equilibrium if the product of the force on the arm on one side is equal to the product of the force on the arm on the other side.
Molecular physics
To the table of contents...
The chemical amount of a substance is found according to one of the formulas:
The mass of one molecule of a substance can be found using the following formula:
Relationship between mass, density and volume:
The basic equation of the molecular kinetic theory (MKT) of an ideal gas:
The definition of concentration is given by the following formula:
There are two formulas for the root mean square speed of molecules:
Average kinetic energy of translational motion of one molecule:
Boltzmann's constant, Avogadro's constant and the universal gas constant are related as follows:
Corollaries from the basic MKT equation:
Equation of state of an ideal gas (Clapeyron-Mendeleev equation):
Gas laws. Boyle-Marriott Law:
Gay-Lussac's Law:
Charles's Law:
Universal gas law (Clapeyron):
Pressure of a mixture of gases (Dalton's law):
Thermal expansion of bodies. The thermal expansion of gases is described by Gay-Lussac's law. The thermal expansion of liquids obeys the following law:
For the expansion of solids, three formulas are used to describe the change in the linear dimensions, area and volume of the body:
Lever equilibrium equation:
F1 × l1 = F2 × l2
It follows from this that the lever is balanced when the magnitudes of the forces applied to its ends are inversely proportional to the arms of these forces.
| The moment of force is a vector quantity, the numerical characteristic of which can be described as the product of the force modulus and the arm. |
Formula for moment of force:
M = F × l, where F is the force modulus, l is the arm length.
The SI unit of torque is newton meter (Nm).
This formula is correct if the force is applied perpendicular to the axis of the lever. If it is applied at an angle, such a case goes beyond the scope of the physics course for the 7th grade and is studied in detail in the 9th grade.
| Rule of Moments: A lever is balanced if the sum of all moments of forces that turn it clockwise is equal to the sum of all moments of forces that turn it in the opposite direction. |
We can say it differently: a lever is in equilibrium if the sum of the moments of all forces applied to it relative to any axis is equal to zero.
M1 + M2 + Mn + … = 0
Magnetism
To the table of contents...
Ampere force acting on a current-carrying conductor placed in a uniform magnetic field is calculated by the formula:
Moment of forces acting on the frame with current:
The Lorentz force acting on a charged particle moving in a uniform magnetic field is calculated by the formula:
Radius of the flight trajectory of a charged particle in a magnetic field:
The induction modulus B of the magnetic field of a straight conductor with current I at a distance R from it is expressed by the relation:
Field induction at the center of a coil with a current of radius R:
Inside a solenoid of length l and number of turns N, a uniform magnetic field is created with induction:
The magnetic permeability of a substance is expressed as follows:
The magnetic flux Φ through the area S of the contour is the value given by the formula:
Induction emf is calculated by the formula:
When a conductor of length l moves in a magnetic field B at a speed v, an induced emf also occurs (the conductor moves in a direction perpendicular to itself):
The maximum value of the induced emf in a circuit consisting of N turns, area S, rotating with angular velocity ω in a magnetic field with induction B:
Coil inductance:
Where: n is the concentration of turns per unit length of the coil:
The relationship between the inductance of the coil, the current flowing through it and its own magnetic flux penetrating it is given by the formula:
Self-induction emf arising in the coil:
Coil energy (generally speaking, this is the energy of the magnetic field inside the coil):
Volumetric magnetic field energy density:
Pressure, pressure force
By applying the same force to an object, you can get different results depending on the area over which this force is distributed. This phenomenon is explained in the 7th grade curriculum by the physical terms “pressure” and “pressure force.”
| Pressure is a quantity equal to the ratio of the force acting on a surface to the area of this surface. The pressure force is directed perpendicular to the surface. |
Pressure formula:
p = F / S, where F is the force modulus, S is the surface area.
The SI unit of pressure is pascal (Pa).
1 Pa = 1 N/m2
It is clear that with the same force of influence, a higher pressure will be experienced by the surface whose area is smaller.
The formula for calculating the pressure force is easy to derive:
F=p×S
In physics problems for grade 7, the force of pressure is usually equal to the weight of the body.
Electrostatics
To the table of contents...
Electric charge can be found using the formula:
Linear charge density:
Surface charge density:
Volumetric charge density:
Coulomb's law (the force of electrostatic interaction between two electric charges):
Where: k is a certain constant electrostatic coefficient, which is determined as follows:
The electric field strength is found by the formula (although more often this formula is used to find the force acting on a charge in a given electric field):
Superposition principle for electric fields (the resulting electric field is equal to the vector sum of the electric fields of its components):
The electric field strength created by a charge Q at a distance r from its center:
Electric field strength created by a charged plane:
The potential energy of interaction of two electric charges is expressed by the formula:
Electrical voltage is simply a potential difference, i.e. The definition of electrical voltage can be given by the formula:
In a uniform electric field there is a relationship between field strength and voltage:
The work of the electric field can be calculated as the difference between the initial and final potential energy of the system of charges:
The work of the electric field in the general case can also be calculated using one of the formulas:
In a uniform field, when a charge moves along its field lines, the work of the field can also be calculated using the following formula:
The definition of potential is given by the expression:
The potential that a point charge or charged sphere creates:
Superposition principle for electric potential (the resulting potential is equal to the scalar sum of the potentials of the fields that make up the resulting field):
For the dielectric constant of a substance, the following is true:
The definition of electrical capacitance is given by the formula:
Capacitance of parallel plate capacitor:
Capacitor charge:
Electric field strength inside a parallel-plate capacitor:
The force of attraction of the plates of a flat capacitor:
Capacitor energy (generally speaking, this is the energy of the electric field inside the capacitor):
Volumetric electric field energy density:
Pressure of gases and liquids
Liquids and gases filling the vessel press on its walls. This pressure depends on the height of the column of a given substance and on its density.
Hydrostatic pressure formula:
р = ρ × g × h, where ρ is the density of the substance, g is the force of gravity, h is the height of the column.
g = 9.8 m/s2
The SI unit of liquid or gas pressure is pascal (Pa).
A homogeneous liquid or gas presses evenly on the walls of the container, since this pressure is created by chaotically moving molecules. And the external pressure exerted on the substance is also evenly distributed throughout its entire volume.
| Pascal's law: pressure exerted on the surface of a liquid or gaseous substance is equally transmitted to any point, regardless of direction. |
The external pressure exerted on a liquid or gas is calculated by the formula:
p = F / S, where F is the force modulus, S is the surface area.
Relative density of one gas to another
Sometimes, to solve a problem, you need to know how to find the molar mass of a gas, for which only its density in air or another gas is reported. This is possible if you know the relative density formula, which is denoted by the letter D.
, where and are some gases.
Example 1
How to determine how many times carbon monoxide is denser than hydrogen?
First, let's find the molar mass of CO and H2:
M(CO) = Mr(CO) = Ar(C) + Ar(O) = 12 + 16 = 28.
M(H) = Mr(H2) = 2 Ar(H) = 2 1 = 2.
.
Answer: Carbon monoxide is 14 times denser than hydrogen.
Example 2
How to calculate the molar mass of a gas x, which is known to be 10 times denser than carbon dioxide CO2?
First, let's calculate the molar mass of carbon dioxide:
M(CO2) = Mr(CO2) = 12 + 2 16 = 44.
Based on the relative density formula, we will calculate the molar mass of the desired gas x.
M(x) = D(x/CO2) M(CO2) = 10 44 = 440 g/mol.
Answer: This gas has a molar mass of 440 g/mol.
Communicating vessels
| Communicating are vessels that have a common bottom or are connected by a tube. The level of homogeneous liquid in such vessels is always the same, regardless of their shape and cross-section. |
If ρ1 = ρ2, then h1 = h2 and ρ1gh1 = ρ2gh2, where:
p—liquid density,
h is the height of the liquid column,
g = 9.8 m/s2.
If the liquid in communicating vessels is heterogeneous, i.e., has different densities, the height of the column in a vessel with a denser liquid will be proportionally smaller.
The heights of columns of liquids with different densities are inversely proportional to the densities.
| A hydraulic press is a mechanism created on the basis of communicating vessels of different sections filled with a homogeneous liquid. Such a device makes it possible to obtain a gain in force for exerting static pressure on parts (compression, clamping, etc.). |
If pressure p1 = f1/s1 is formed under piston 1, and pressure p2 = f2/s2 is formed under piston 2, then, according to Pascal’s law, p1 = p2
Hence,
The forces acting on the hydraulic press pistons F1 and F2 are directly proportional to the areas of these pistons S1 and S2.
In other words, the force of piston 1 is greater than the force of piston 2 as many times as its area is greater than the area of piston 2. This makes it possible to balance a much larger force in a hydraulic machine using a small force.
Hydrostatics
To the table of contents...
The definition of pressure is given by the following formula:
The pressure created by the liquid column is determined by the formula:
But often it is also necessary to take into account atmospheric pressure, then the formula for the total pressure at a certain depth h in the liquid takes the form:
Ideal hydraulic press:
Any hydraulic press:
Efficiency for a non-ideal hydraulic press:
Archimedes' force (buoyancy force, V - volume of the immersed part of the body):
Archimedes' Law
| The buoyant force of a body immersed in a liquid or gas is equal to the weight of this liquid or gas in the same volume as that of this body. |
Archimedean force formula:
Fa = ρ × g × V, where ρ is the density of the liquid, V is the volume of the liquid, g is the acceleration 9.8 m/s2.
Archimedes' law helps to calculate how a body will behave when immersed in media of different densities. The following statements are true:
- if the density of the body is higher than the density of the medium, it will sink to the bottom;
- if the density of the body is lower, it will float to the surface.
In other words, the body will rise to the surface if the Archimedean force is greater than the force of gravity.
Molar volume
Above we found the amount of a substance through molar mass, but for gases this can also be done through molar volume. According to Avogadro's law, an amount of any gas equal to 1 mole will occupy the same volume if the gases are considered at the same temperature and pressure.
Under standard physical conditions - temperature 0°C and pressure 1 atm or 760 mmHg, 1 mole of gas occupies a volume of 22.4 liters.
Molar volume is the volume of gas taken in the amount of 1 mole. It is designated Vm.
Under normal conditions, Vm = 22.4 l/mol.
The values of the molar and actual volume of a gas help to find the amount of a substance.
, where is the actual volume of gas, and is the molar volume.
Example 1
How many moles are contained in 120 liters of gas under normal conditions?
Let's calculate using the formula mole.
Answer: 120 liters of any gas under standard conditions contain 5.36 moles.
Work, energy, power
| Mechanical work is a scalar quantity that is equal to the product of the displacement of the body by the modulus of the force under the influence of which the displacement was performed. It is assumed that the displacement occurred in the same direction in which the force acts. |
Formula for work in a physics course for grade 7:
A = F × S, where F is the acting force, S is the path traveled by the body.
The SI unit of work is joule (J).
The concept of power describes the speed at which mechanical work is performed. It tells you how much work was done per unit of time.
| Power is a scalar quantity equal to the ratio of work to the time period required to complete it. |
Power formula:
N = A / t, where A is the work, t is the time it was completed.
Power can also be calculated by knowing the force acting on a body and the average speed of movement of this body.
N = F × v, where F is force, v is the average speed of the body.
The SI unit of power is watt (W).
A body can do any work if it has energy - kinetic and/or potential.
- Kinetic energy is the energy of motion of a body. It talks about how much work needs to be done to give a body a certain speed.
- Potential is the energy of interaction of a body with other bodies or interaction between parts of one whole. The potential energy of a body raised above the Earth characterizes how much work must be done by gravity to lower this body back to zero.
Table with formulas in physics for grade 7 for calculating kinetic and potential energy:
| Kinetic energy | Proportional to the mass of the body and the square of its speed. | Ek = mv2/2 |
| Potential energy | Equal to the product of the mass of a body raised above the Earth by the acceleration of gravity and the height of the lift. | Ep= mgh |
| Total mechanical energy | It is made up of kinetic and potential energy. | E = Ek+Ep |
| Conservation and conversion of energy | If mechanical energy does not transform into other forms, then the sum of potential energy and kinetic energy is a constant. | Ek+ Ep= const |
In order to understand what part of the work done was useful, the coefficient of performance or efficiency is calculated. With its help, the effectiveness of various mechanisms, tools, etc. is determined.
| The efficiency factor (COP) reflects the useful part of the work performed. It can also be expressed through the ratio of useful energy used to the total amount of energy received. |
How to determine molar mass
This quantity is closely related to concepts such as relative atomic and molecular masses. Precisely relative, because the absolute mass of a molecule or atom of a substance in chemistry is not used to solve problems - these are too small values.
The relative atomic mass of a substance (Ar) shows how many times its atom is larger than 1/12 of a carbon atom. This value for each chemical element can be seen in the periodic table.
The relative molecular mass (Mr) is the sum of the Ar of each atom in the molecule of a substance, taking into account the indices. It shows how much the mass of a molecule is greater than 1/12 of a carbon atom.
, where is the number of atoms.
Let's look at examples.
In a molecule of sodium chloride NaCl there is 1 sodium atom and 1 chlorine atom, with Ar(Na) = 23, Ar (Cl) = 35.5.
Mr(NaCl) = 23 + 35.5 = 58.5.
A NaNO2 molecule contains 1 sodium atom, 1 nitrogen atom and 2 oxygen atoms.
Ar(Na) = 23, Ar(N) = 14, Ar(O) = 16.
Mr(NaNO2) = 23 + 14 + 16 2 = 69.
Actually, nothing else is required to calculate the molar mass.
Important
The molar mass of a substance is numerically equal to the relative molecular mass. But these two concepts should not be confused - they have different physical meanings. Molar mass characterizes 1 mole, and relative molecular mass characterizes 1 molecule.
Body mass
To get acquainted with the physical nature of mass, the easiest way is to conduct an experiment with bodies of the same shape and size, but different masses. For example, you can take a small balloon, a soccer ball and a cast iron ball of the same size (20-25 cm in diameter).
Despite the same size, these three bodies will behave completely differently when thrown. After hitting the balloon, it will immediately acquire a speed almost equal to the speed of the hand. But then its speed will decrease very quickly due to air resistance. After being hit, a soccer ball will fly much further - tens of meters. But it will be more difficult to give it the same initial speed as a balloon. If you take a cast iron cannonball, then the muscle strength is only enough to throw it a couple of meters.
Why do the three examples above produce completely different results? The answer lies in the difference in mass of the objects used.
This experience shows that in order to impart a certain speed to the body, it is necessary to expend effort, and during acceleration the body will “resist” acceleration. This “acceleration resistance” is called body inertia. The physical quantity characterizing inertia is called mass.
Rice. 1. Body weight
Uniform movement around a circle
To the table of contents...
As an addition, in the table below we present all possible relationships between the characteristics of a body rotating uniformly in a circle (T – period, N – number of revolutions, v – frequency, R – radius of the circle, ω – angular velocity, φ – angle of rotation (in radians), υ – linear speed of the body, an – centripetal acceleration, L – length of the circular arc, t – time):
Fundamentals of the special theory of relativity (STR)
To the table of contents...
Relativistic length reduction:
Relativistic extension of event time:
Relativistic law of addition of velocities. If two bodies are moving towards each other, then their speed of approach is:
Relativistic law of addition of velocities. If bodies move in the same direction, then their relative speed is:
Body resting energy:
Any change in body energy means a change in body weight and vice versa:
Total body energy:
The total energy of the body E is proportional to the relativistic mass and depends on the speed of the moving body; in this sense, the following relationships are important:
Relativistic mass increase:
Kinetic energy of a body moving at relativistic speed:
There is a relationship between the total energy of the body, rest energy and momentum: