HOW TO CALCULATE THE WEIGHT OF METAL - FORMULAS AND RECOMMENDATIONS

If there is no possibility of direct weighing, the weight of scrap metal can be determined in other ways. The most accurate result will be given by calculation, but other possibilities should not be neglected.

So, in order not to burden readers with unnecessary formulas, which will still be there, but below, we will immediately designate the formulas for calculating the most popular products from rolled steel and pipes - rolled pipes. Here you will not find an online calculator for calculating weight, only formulas that you remember once you no longer have to use special calculators. For example, when dismantling metal structures or a chimney, you don’t always have a computer, the Internet or a reference book at hand, but the structures are all welded from rolled steel here and our formulas will help out!

Formula to calculate pipe weight

M=(Ds)*s*0.02466

, Where

M— weight of one linear meter of pipe, kg;
D is the outer diameter of the pipe being calculated, mm;
s—pipe wall thickness, mm;
0,02466 —coefficient for steel density equal to 7.850 g/cm3.

This formula is very accurate. You can calculate the weight of the pipe and compare the calculated weight with the theoretical one in any range and the value according to the formula will be more accurate! You can also calculate

Calculating the weight of a sheet of metal

M=S*7.85

, Where

M—mass of steel sheet, kg;
S is the area of the calculated sheet, in square meters;
7.85 - weight of a sheet 1 mm thick and 1 square meter in area, in kilograms

This way you can calculate the weight of a sheet of metal of any size, for which you can calculate the area. The accuracy of calculations using this formula is higher than the theoretical mass in reference books, because in the assortment, when calculating the mass of metal, the program rounds the values. Well, how to find out the area of a sheet (of any shape - square, rectangle, parallelepiped, trapezoid, rhombus, etc.) - every person who has graduated from high school should know.

Then data in meters or tons is entered into one of the fields

If you enter values in the "meters" field ("square meters" to find out the weight of the sheet), then you will know the total weight of the entire length (for example, the weight of the reinforcement).

If you are interested in calculating length by weight, then you need to enter data in the “tons” field.

How to calculate the weight of reinforcement and rod

For a circle, rod, smooth reinforcement, the formula for calculating the mass will be as follows:

M=(0.02466*D2)/4

, Where

M—weight of 1 linear meter of circle/reinforcement/rod, kg;
D—circle diameter;
0,02466 —coefficient for steel density equal to 7.850 g/cm3

To calculate the weight of corrugated reinforcement (A2, A3), you can and should use the same formula! There will be no discrepancies with the theoretical mass, despite the different cross-sectional designs.

It is, of course, impossible to calculate such a pile of scrap metal using formulas without weighing

Definition and use of density

As you know, to find the density of a substance, its mass is divided by its volume. Density is a physical and chemical characteristic of a substance. She is constant. Materials for industrial production must meet this indicator. To denote it, it is customary to use the Greek letter ρ. The density of iron is 7874 kg/m³, nickel - 8910 kg/m³, chromium - 7190 kg/m³, tungsten - 19250 kg/m³. Of course, this applies to hard alloys. In the molten state, substances have different characteristics.

General approaches or a little boring theory

To determine the weight of any object, simply multiply its volume by its specific gravity. If everything is more or less clear with specific gravity, then volume is more difficult to determine (if you do not consider such simple shapes as a cube). The most general principle for calculating volume is Gulden's principle, when the cross-sectional area of an object is multiplied by its height. There are also usually no problems with the height of the metal structure; it is easy (or almost easy) to measure directly, especially if the height section is constant. This can be done for steel pipes of any section and profile, I-beams, channels, angles, etc. We will consider the method for determining the mass of metal objects of complex and variable shapes later.

How to find out the mass of a pipe

Finding the parameter of a metal pipe of any diameter is carried out similarly to the method for a round profile. Calculate the difference in the areas of two circles. The first has the outer radius of the pipe. The second has the inner radius of the pipe.

The resulting difference is multiplied by the length of the pipe, calculating the volume of metal. Multiplying by the density of steel, the mass of a pipe of a given length is found. Operations with non-ferrous metal products are simplified through the use of a conversion factor.

Pipe weight

When working with ready-made tables, you should find data for a 1 m bar with a radius equal to the outer diameter. Calculate the diameter of the rod, which is equal to the internal diameter. Subtract the smaller value from the larger value to get the desired result. It should be multiplied by the length of the sample.

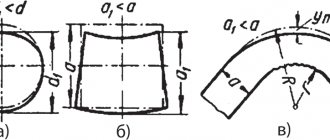
Volume of a truncated pyramid

The enclosing caps, protective latches and doors have the shape of a truncated pyramid. In such situations, a dependency is used:

, Where:

h – height of the truncated pyramid;
F is the area of its larger base;
f is the area of the smaller base.

If the pyramidal part of the structure sold for scrap is somewhat deformed, then the missing volume is added or removed from each side.

Online metal calculator

Rolled metal includes all products that have been hot or cold rolled on special machines. Today there are many species with different characteristics. It is impossible to remember the density of each metal and alloy. Therefore, it is extremely difficult to calculate tonnage. To do this, use the metal calculator on our website. He will quickly make calculations based on the characteristics of the product.

Volume of wedge and obelisk

The wedge in the technique is often a pentahedron, the base of which is a rectangle, and the side faces are isosceles triangles or trapezoids. The formula for calculating the volume of a wedge is:

, Where:

a – side of the base of the wedge foot;
а1 – width of the wedge top;
b – wedge thickness;
h is the height of the wedge.

An obelisk is a hexagon, the base of which is rectangles located in parallel planes. The opposite faces are symmetrically inclined to the base of the obelisk. Volume of this geometric body:

, Where:

a and b – dimensions of the length and width of the larger base of the obelisk;
and a1 and b1 – the smaller base of the obelisk;
h – height of the obelisk.

Volumes of rolled profiles

Most often it is necessary to determine the weight of tees, I-beams, channels, and angles. The following dependencies are used for this:

For the brand

,where b and b1 are the width of the shelf and wall of the tee, respectively; h and h1 – thickness of the base and flange of the tee; H – height of the T-bar fragment;

For I-beam

,where H is the height/length of the I-beam; a – I-beam wall thickness; с and с1 – thickness of the I-beam flange at the base and at the end, respectively;

For the corner

,where H is the length of the corner; l1 – angle thickness; h1 and h2, respectively, are the width of each shelf.

Determination of the estimated mass of the composition

The mass of the composition is one of the most important indicators affecting

efficiency of the railway. The mass of the composition determines

carrying capacity of lines, cost and efficiency of transportation, and

also specific consumption of fuel or electricity (for EPS) for traction of trains.

The mass of the train is determined for each section of the route or stage from

conditions for the fullest use of locomotive power and movement

at a speed that ensures long-term operation.

The mass of the train is determined by the calculated lift using the formula, t:

Q= = ≈ 5000t (2.2) where

Fcr – estimated traction force of a given locomotive, N.;

P – design mass, t;

– main specific resistance to movement of the locomotive in traction mode, N/kN;

– main specific resistance to movement of the train (loaded cars), N/kN;

– steepness of the estimated rise, ‰;

g – free fall acceleration (g= 9.81 m/s2).

Values are calculated with an accuracy of two decimal places.

=1.9+0.348+0.47=2.7

=0.7+
=1.3
=0.7+
=1.3
The main specific resistance to the movement of the train is determined by

formula:

= 1.3*0.1+1.3*0.9 = 1.3 (2.3) where

and – the main specific resistance to movement of 4-axle and 8-axle cars, respectively, N/kN;

and – weight shares in the composition of the corresponding cars (set as percentages in the assignment for the course work, which must be converted into shares).

The axle load of the cars is calculated using the formula:

(2.4) where

– average gross weight of the corresponding cars (see task form), t;

– axle of the corresponding types of cars.

=17,5

Substituting the obtained values of resistance to movement of cars into expression (2.3), we find the main specific resistance to movement of the train.

After this, the calculated mass of the composition is determined using formula (2.2).

The resulting value is rounded up or down by multiples of 50 tons.

Checking the calculated mass.

Checking the calculated mass to overcome the kinetic

Lifting.

After determining the mass of the train when following a calculated rise with a uniform speed, it is checked for the possibility of passing a steeper kinetic (high-speed or inertial) rise, taking into account the use of kinetic energy when moving at a decelerating speed in an analytical way.

The analytical method of checking is to determine the length of the path that the train must cover in traction mode using kinetic energy when reducing speed from the highest at the beginning of the high-speed rise Vн to the calculated one at the end of it (Vн = Vр) and compare it with the length of this rise (Sk).

To increase the accuracy of the calculation, the speed change interval should be taken equal to 10 km/h.

The distance covered by the train during the time of speed change from Vн to Vк is determined by the formula:

where where 4.17 is a coefficient taking into account the acceleration of the train, km/h2; Vкj,Vн.j – train speed at the end and beginning of the specified speed interval on the tested kinetic rise, km/h; average specific resultant force applied to the train within the selected speed interval, N/kN.

The speed at the beginning of a kinetic rise is determined by methods known in traction calculations, depending on the steepness of the elements located in front of this rise, and in the course work the speed at the beginning of a kinetic rise is taken based on an analysis of the path profile within the range of 60...80 km/h.

The specific thrust force is determined by the expression:

(2.6)

where Fk is the traction force, determined from the traction characteristics of locomotives for the average speed of the interval Vavj, N.

The average speed for the selected movement interval is determined by the formula:

(2.7)

The specific retarding force of speeds is found by the formula:

, (2.8)

where , are the main specific resistance to movement of the locomotive and train, determined for the average speed of intervals according to the formulas given above, N/kN; ik – kinetic rise, ‰.

The path segments obtained during the speed reduction in each interval are summed up and compared with the length of the kinetic rise, i.e.:

(2.9)

1050m ≤ 1895m

If condition (2.9) is satisfied, then we can conclude:

“A train with a locomotive of the VL 80R series and a mass of the train Q = 5000 tons overcomes a kinetic rise with a steepness ik = -10 ‰ and a length Sk = 1050 km when the speed changes from vн = 80 to vк = 70 km/h and the mass of the train should be considered determined for of this area of locomotive operation."