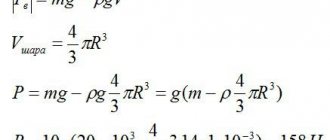A spring pendulum is an oscillatory system that consists of a body suspended from a spring. This system is capable of free oscillations.
Such systems are quite widespread due to their functional flexibility. Mechanisms based on such pendulums are often used as elements of automation equipment.
Among other things, they have found application in contact fuses of various ammunition, and as accelerometers in missile control circuits. They are also actively used in safety valves installed in pipelines.
What is a spring pendulum
In physics, a spring pendulum is a system that performs oscillatory movements under the influence of elastic force.
The following notations are accepted:
- m—body weight;
- k is the spring stiffness coefficient.
General view of the pendulum:
Features of spring pendulums are:
- Combination of body and spring.
The mass of the spring is usually neglected in calculations. The role of a body can be played by various objects. They are influenced by external forces. The load can be attached in different ways. The coils of the spring with which it begins and ends are made taking into account the increased load;
- Any spring has an initial position, a limit of compression and extension.
At maximum compression there is no gap between the turns. When it is stretched to its maximum, irreversible deformation occurs;
- Full mechanical energy appears with the onset of the reversible deformation process.
At this moment, there is no elastic force acting on the object;
- Oscillatory movements occur under the influence of elastic force.
The scale of the influence is determined by several factors (type of alloy, arrangement of turns, etc.). Since both compression and tension can occur, we can conclude that the elastic force acts in two opposite directions;
- The speed in the plane of its movement depends on the mass of the body, the magnitude and direction of the applied force.
For example, if you hang a load on a spring and, after stretching it, release it, the load will move in two planes: vertically and horizontally.
Control questions
What is deformation? What deformations are called elastic? Give examples of elastic deformations.
What is the physical essence of elastic forces?
State Hooke's law? When is it fair?
Explain the qualitative stress diagram. What is the limit of proportionality, elasticity and strength?
What are elastic hysteresis and elastic aftereffect?
What is the physical meaning of Young's modulus and shear modulus?
What is elastic aftereffect?
Derive expressions for strains under all-round tension.
What is Poisson's ratio?
Determine the energy of the deformed body.
What is elastic energy density called? Obtain formulas for this energy under tension and shear.
A. mv²/2 B.mv C.mgh D. kx²/2 2. What is the name of the unit of kinetic energy expressed through the basic units of the International System? A.1kg·m B.1kg·m/s C.1kg·m²/s D.1kg·m²/s² 3. What is the kinetic energy of a body weighing 3 kg moving at a speed of 4 m/s?
Read also: Why does the washing machine vibrate a lot during the spin cycle?
A. 6 J. B. 12 J. B. 24 J. G.48J.
4. How will the potential energy of an elastically deformed body change when its deformation increases threefold?
À. Will not change. B. Will increase 3 times. . Will increase 9 times. D. Will increase 27 times.
Two cars with the same masses m move with speeds v and 3v relative to the Earth in the same direction. What is the kinetic energy of the second car in the frame of reference associated with the first car?
A.mv² B.2mv² C.3mv² D.4mv² 6.What is the name of the unit of work expressed through the basic units of the International System? A.1kg B.1kg m/s C.1kg m/s² D.1kg m²/s² 7. By what formula should the work of force F be calculated if there is an angle a between the direction of force and displacement S? A.(F/S)·cosα B.F·S·sinα C.F·S·cosα D.(F·S)·sinα
9. A body weighing 1 kg with a force of 30 N rises to a height of 5 m. What is the work done by this force?
A .0 J. B. 50 J. B. 100 J. G. 150 J.
The kinetic energy of the body at the moment of throwing is 200 J. Determine to what height from the surface of the earth the body can rise if its mass is 500 g.
A tower crane lifts a concrete slab weighing 2 tons to a height of 15 m. What is the work done by gravity acting on the slab?
Types of spring pendulums
There are two types of this system:
- Vertical
pendulum - the body is quite strongly influenced by gravity. This influence causes an increase in the inertial movements that the body makes at the starting point.
- Horizontal
- in this case, when moving, a frictional force begins to act on the load, which arises due to the fact that the load lies on the surface.
Elastic force in a spring pendulum
Before deformation begins, the spring is in an equilibrium state. The applied force can either stretch or compress it.
By applying the law of conservation of energy to a spring pendulum, we can calculate the elastic force in it. Elasticity is directly proportional to the distance over which the load has shifted.
The elastic force can be calculated as follows:
F control
= - k*x
where k is the spring stiffness coefficient (N\m),
x – displacement (m).
Equations of oscillations of a spring pendulum
Free oscillations of a spring pendulum are described using the harmonic law.
If we assume the probability that the oscillations occur along the X axis, and Hooke’s law is satisfied, then the equation will take the form:
F(t) = ma(t) = — mw2x(t),
where w is the radial frequency of the harmonic vibration.
To calculate vibrations, taking into account all probabilities, the following formulas are used:
Question 5
Question text
The capacitor of the oscillating circuit is charged from a constant voltage source and then connected to coils with different inductances: L 1, L 2, L 3. Select words in the second column of the table that correctly characterize changes in the parameters of harmonic oscillations in the oscillating circuit when the inductance of the coils decreases in such experiments
Read also: Metals with low thermal conductivity
For each quantity, determine the corresponding nature of the change:
Write down the selected numbers for each physical quantity in the table. The numbers in the answer may be repeated.
| Amplitude of capacitor charge oscillations | Oscillation frequency | Amplitude of force fluctuations |
Period and frequency of free oscillations of a spring pendulum
When developing projects, the period of oscillation and its frequency are always determined. To measure them, formulas known in physics are used.
The change in cyclic frequency will be shown by the formula shown in the figure:
Factors on which frequency depends:
- Elasticity coefficient.
This coefficient is affected by the number of turns, their diameter, the distance between them, the length of the spring, the stiffness of the alloy used, etc.
- Cargo weight.
The resulting inertia and speed of movement depend on this factor.
Moment of force and moment of impulse about the axis
The deformation of the spring is also considered taking into account the moment of force and momentum relative to the axis. These two parameters allow you to calculate all the required indicators with higher accuracy. A fairly common question is what the moment of force is - a vector quantity that is determined by the vector product of the radius and the vector of the applied force.
Momentum is a quantity that is used to determine the amount of rotational motion.
Among the features of this indicator are the following:
- Rotation mass. An object can have different masses.
- Distribution relative to the axis. The axis can be located at different distances from the object itself.
- Rotational speed. This property is considered the most important; depending on the design, it can be constant or change.
The calculation of each indicator is carried out by applying the appropriate formula. In some cases, the required input data is measured, without which calculations will not be possible.
Energy of a spring pendulum
When considering the vibrations of bodies, it is taken into account that the load moves in a straight line. The total mechanical energy of the body at each point of the trajectory is a constant and equals the sum of its potential energy and kinetic energy.
Potential energy:
Kinetic energy:
Total Energy:
The calculation has its own peculiarities. When carrying it out, several conditions must be taken into account:
- Oscillations take place in two planes: vertical and horizontal.
- Zero potential energy is chosen as the equilibrium position. While in this position, the spring retains its shape.
- The influence of friction force is not taken into account in the calculation.
Spring potential energy and kinetic energy - what is it, what is the formula?
Many mechanisms use the potential and kinetic energy of a spring. They are used to perform various actions. In individual units, they fix the parts in a certain position, preventing them from being shifted in any direction (the revolver drum relative to the body). Other spring systems return the actuator to its original position (the trigger of a handgun). There are devices where units with flexible properties move to a stable position (mechanical stabilizers).
The work involves changing the geometric parameters of an elastic body. By applying a load, the elastic part is forced to compress (stretch or bend). In this case, energy storage is observed. The return action is accompanied by an increase in speed. At the same time, kinetic energy increases.
Considering a spring as an energy storage device, one should note its distinctive properties from other physical bodies that can accumulate energy potential. Traditionally, the following is understood: to accumulate potential for subsequent movement, it is necessary to perform a movement in a force field:
Ep = F ⋅ l, J (N m),
where Ep is the potential energy of position, J;
F is the force acting on the body, N;
l is the amount of displacement in the force field, m.
Energy (work) is measured in Joules. The value represents the product of force (N) and displacement (m).
If we consider the condition in the gravitational field, then the magnitude of the force is found by the product of the acceleration of gravity and the mass. Here the weight force is found taking into account g:
Ep = G ⋅ h = m ⋅ g ⋅ h, J
here G is body weight, N;
m—body weight, kg;
g is the acceleration of free fall. On Earth, this value is g = 9.81 m/s².
If the spring is detuned, then the force F must be determined as a value proportional to the displacement:
F = K ⋅ x, N,
where k is the elastic modulus, N/m;
x — displacement during compression, m.
The amount of compression can vary in magnitude, so mathematicians have proposed analyzing such phenomena using infinitesimal quantities (dx).
In the presence of a non-constant force depending on the displacement, the differential equation will be written as:
dEп = k ⋅ x ⋅ dx
here dEп is elementary work, J;
dx - elementary compression increment, N.
The integral equation for finite displacement will be written in the form. Below is the output of the formula:
The limits of integration are the interval from 0 to x. A deformed spring gains energy reserves
Finally, the formula for calculating the magnitude of the potential energy of compression (stretching or bending) of the spring will be written as: