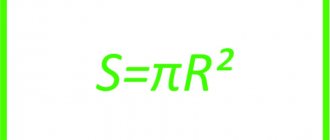The correct choice of electrical cable to power electrical equipment is the key to long-term and stable operation of installations. Using the wrong wire has serious negative consequences.
The physics of the process of damage to an electrical line due to the use of an unsuitable wire is as follows: due to the lack of space in the cable core for the free movement of electrons, the current density increases; this leads to excess energy release and an increase in the temperature of the metal. When the temperature gets too high, the line's insulating sheath melts, which can cause a fire.
To avoid trouble, you must use a cable with cores of suitable thickness. One way to determine the cross-sectional area of a cable is to start from the diameter of its cores.
Volumetric figures
It is known from stereometry that a three-dimensional figure of absolutely any type is limited by a number of surfaces. For example, for polyhedra such as a prism and a pyramid, these surfaces are polygonal sides. For a cylinder and a cone, we are talking about surfaces of rotation of cylindrical and conical figures.
You will be interested in: What does it mean to be reputed: interpretation, synonyms
If we take a plane and intersect the surface of a three-dimensional figure with it in an arbitrary manner, we will obtain a section. Its area is equal to the area of the part of the plane that will be located inside the volume of the figure. The minimum value of this area is zero, which is realized when the plane touches the figure. For example, a section that is formed by a single point is obtained if the plane passes through the top of a pyramid or cone. The maximum value of the cross-sectional area depends on the relative position of the figure and the plane, as well as on the shape and size of the figure.
Below we will consider how to calculate the areas of the formed sections for two figures of revolution (cylinder and cone) and two polyhedra (pyramid and prism).
Selection by table
Knowing the diameter of the wire, you can determine its cross-section using a ready-made dependence table. The table for calculating the cable cross-section by core diameter looks like this:
| Conductor diameter, mm | Conductor cross-section, mm2 |
| 0.8 | 0.5 |
| 1 | 0.75 |
| 1.1 | 1 |
| 1.2 | 1.2 |
| 1.4 | 1.5 |
| 1.6 | 2 |
| 1.8 | 2.5 |
| 2 | 3 |
| 2.3 | 4 |
| 2.5 | 5 |
| 2.8 | 6 |
| 3.2 | 8 |
| 3.6 | 10 |
| 4.5 | 16 |
When the cross-section is known, it is possible to determine the permissible power and current values for copper or aluminum wire. In this way, it will be possible to find out what load parameters the current-carrying core is designed for. To do this, you will need a table of the dependence of the cross section on the maximum current and power.
| In the air (trays, boxes, voids, channels) | Section, sq. mm | In the ground | |||||||||
| Copper conductors | Aluminum conductors | Copper conductors | Aluminum conductors | ||||||||
| Current. A | power, kWt | Tone. A | power, kWt | Current, A | power, kWt | Current. A | Power, kWt | ||||
| 220 (V) | 380(V) | 220(V) | 380(V) | 220(V) | 380(V) | 220(V) | |||||
| 19 | 4.1 | 17.5 | 1,5 | 77 | 5.9 | 17.7 | |||||
| 35 | 5.5 | 16.4 | 19 | 4.1 | 17.5 | 7,5 | 38 | 8.3 | 75 | 79 | 6.3 |
| 35 | 7.7 | 73 | 77 | 5.9 | 17.7 | 4 | 49 | 10.7 | 33.S | 38 | 8.4 |
| *2 | 9.7 | 77.6 | 37 | 7 | 71 | 6 | 60 | 13.3 | 39.5 | 46 | 10.1 |
| 55 | 17.1 | 36.7 | 47 | 9.7 | 77.6 | 10 | 90 | 19.8 | S9.7 | 70 | 15.4 |
| 75 | 16.5 | 49.3 | 60 | 13.7 | 39.5 | 16 | 115 | 753 | 75.7 | 90 | 19,8 |
| 95 | 70,9 | 67.5 | 75 | 16.5 | 49.3 | 75 | 150 | 33 | 98.7 | 115 | 75.3 |
| 170 | 76.4 | 78.9 | 90 | 19.8 | 59.7 | 35 | 180 | 39.6 | 118.5 | 140 | 30.8 |
| 145 | 31.9 | 95.4 | 110 | 74.7 | 77.4 | 50 | 775 | 493 | 148 | 175 | 38.5 |
| ISO | 39.6 | 118.4 | 140 | 30.8 | 97.1 | 70 | 775 | 60.5 | 181 | 710 | 46.7 |
| 770 | 48.4 | 144.8 | 170 | 37.4 | 111.9 | 95 | 310 | 77.6 | 717.7 | 755 | 56.1 |
| 760 | 57,7 | 171.1 | 700 | 44 | 131,6 | 170 | 385 | 84.7 | 753.4 | 795 | 6S |
| 305 | 67.1 | 700.7 | 735 | 51.7 | 154.6 | 150 | 435 | 95.7 | 786.3 | 335 | 73.7 |
| 350 | 77 | 730.3 | 770 | 59.4 | 177.7 | 185 | 500 | 110 | 379 | 385 | 84.7 |
Converting watts to kilowatts
In order to correctly use the table of wire cross-section versus power, it is important to correctly convert watts to kilowatts.
1 kilowatt = 1000 watts. Accordingly, to obtain the value in kilowatts, the power in watts must be divided by 1000. For example, 4300 W = 4.3 kW.
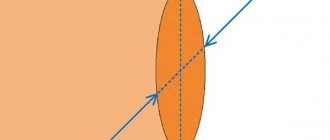
Cylinder
A circular cylinder is a figure of rotation of a rectangle around any of its sides. The cylinder is characterized by two linear parameters: base radius r and height h. Below is a schematic diagram of what a circular straight cylinder looks like.
There are three important types of section for this figure:
- round;
- rectangular;
- elliptical.
An elliptical is formed as a result of a plane intersecting the side surface of a figure at a certain angle to its base. The circular is the result of the intersection of the cutting plane of the side surface parallel to the base of the cylinder. Finally, a rectangular one is obtained if the cutting plane is parallel to the axis of the cylinder.
The circular cross-sectional area is calculated by the formula:
S1 = pi*r2
The area of the axial section, that is, the rectangular section that passes through the axis of the cylinder, is determined as follows:
S2 = 2*r*h
Features of electrical wires
With all the variety of cable products and a huge selection of wires for laying electrical networks, there are selection rules. It is not necessary to memorize all brands of cables and wires; you need to be able to read and decipher their markings. First, it’s worth figuring out the difference between a wire and a cable.
Wire – A conductor used to connect two sections of a circuit. May have one or more conductive wires. The veins can be:
- naked;
- isolated;
- single-core;
- stranded.
Bare lines are used where touching live wires is impossible. In most cases they are used for overhead power lines.
The insulating coating is used in one or two layers. Wires that have two or three conductors in double insulation are confused with a cable. The confusion occurs due to the fact that insulation covers each core, and on the outside there is a general polymer or other coating. Such conductors are used inside electrical devices, panels or cabinets. In everyday life, they are hidden in the wall or laid in special channels.
Insulated products are used everywhere. Depending on the degree of electrical safety of the room and the installation location, the insulation class is selected.
Stranded conductors are used where small radius bends are required when laying complex routes where single-core analogues cannot pass. This type of current conductors is convenient to install in cable ducts. Single-core wires are more difficult to bend in such conditions, force must be applied, and there is a risk of damage to the wire.
For your information. Marking APPV 3*2.5 means a wire with aluminum conductors, polyvinyl chloride insulation, flat, having a dividing base. The meaning of the marking is clarified in the reference literature.
In terms of structure, a cable consists of several individually insulated strands placed in a protective outer layer of dielectric material. The space between the cores and the shell is filled with paper tapes, plastic threads or cable yarn to prevent sticking. Additionally, the product can be reinforced with armor made of tapes or steel braiding to protect against mechanical damage.
Cone sections
A cone is a figure of rotation of a right triangle around one of its legs. The cone has one top and a round base. Its parameters are also radius r and height h. An example of a cone made from paper is shown below.
There are several types of conic sections. Let's list them:
- round;
- elliptical;
- parabolic;
- hyperbolic;
- triangular.
They replace each other if you increase the angle of inclination of the cutting plane relative to the circular base. The easiest way to write down the formulas for the cross-sectional area of a circular and triangular one.
A circular section is formed as a result of the intersection of a conical surface with a plane that is parallel to the base. The following formula is valid for its area:
S1 = pi*r2*z2/h2
Here z is the distance from the top of the figure to the formed section. It can be seen that if z = 0, then the plane passes only through the vertex, so the area S1 will be zero. Since z
Triangular is obtained when the plane intersects the figure along its axis of rotation. The shape of the resulting section will be an isosceles triangle, the sides of which are the diameter of the base and two generatrices of the cone. How to find the cross-sectional area of a triangular? The answer to this question will be the following formula:
S2 = r*h
This equality is obtained if we apply the formula for the area of an arbitrary triangle through the length of its base and height.
Area of a circle circumscribed around a square
It is very easy to find the area of a circle circumscribed around a square.
To do this, you only need the side of the square and knowledge of simple formulas. The diagonal of the square will be equal to the diagonal of the circumscribed circle. Knowing the side a, it can be found using the Pythagorean theorem: from here. After we find the diagonal, we can calculate the radius: . And then we’ll substitute everything into the basic formula for the area of a circle circumscribed around a square:
Let's consider an example of calculating the area of a circle circumscribed around a square. Problem: given a square inscribed in a circle. Its side is a = 4 cm. Find the area of the circle. First, let's calculate the length of the diagonal d. Now we substitute the data into the formula
Knowing a few simple rules and the Pythagorean theorem, we were able to calculate the area of a circle circumscribed around a square.
Prism sections
A prism is a large class of figures that are characterized by the presence of two identical polygonal bases parallel to each other, connected by parallelograms. Any cross section of a prism is a polygon. Due to the variety of figures under consideration (oblique, straight, n-gonal, regular, concave prisms), the variety of their sections is also great. Below we will consider only some special cases.
If the cutting plane is parallel to the base, then the cross-sectional area of the prism will be equal to the area of this base.
If the plane passes through the geometric centers of the two bases, that is, it is parallel to the lateral edges of the figure, then a parallelogram is formed in the section. In the case of straight and regular prisms, the type of section under consideration will be a rectangle.
Units
Square meters
Area is measured in SI units in square meters. One square meter is the area of a square with a side of one meter.
Read also: Types of buses in computer architecture
Unit square
A unit square is a square with sides of one unit. The area of a unit square is also equal to one. In a rectangular coordinate system, this square is located at coordinates (0,0), (0,1), (1,0) and (1,1). On the complex plane, coordinates are 0, 1, i
and i
+1, where
i
is an imaginary number.
Ar or weaving, as a measure of area, is used in the CIS countries, Indonesia and some other European countries, to measure small urban objects such as parks when a hectare is too large. One are is equal to 100 square meters. In some countries this unit is called differently.
Hectare
Real estate, especially land, is measured in hectares. One hectare is equal to 10,000 square meters. It has been in use since the French Revolution, and is used in the European Union and some other regions. Just like the macaw, in some countries the hectare is called differently.
In North America and Burma, area is measured in acres. The hectares are not used there. One acre is equal to 4046.86 square meters. An acre was originally defined as the area that a farmer with a team of two oxen could plow in one day.
Arc length
Consider the circular arc shown in Figure 3 and denote its length by the symbol L(α), where the letter α denotes the value of the corresponding central angle.
Fig.3
In the case where the value α is expressed in degrees, the proportion is valid
from which the equality follows:
In the case where the value α is expressed in radians, the proportion is valid
from which the equality follows:
Video
| Electrical resistance | |
| R | |
| Dimension | L 2 MT −3 I −2 (SI); TL −1 (SGSE, Gaussian system); LT −1 (SGSM) |
| Units | |
| SI | Ohm |
| SSSE | stat, s/cm |
| SGSM | abom, sm/s |
| Classical electrodynamics |
| Electricity Magnetism |
| See also: Portal:Physics |
Electrical resistance
- a physical quantity that characterizes the property of a conductor to prevent the passage of electric current and is equal to the ratio of the voltage at the ends of the conductor to the strength of the current flowing through it.
Resistance for alternating current circuits and for alternating electromagnetic fields is described by the concepts of impedance and characteristic impedance. Resistance (resistor) is also called a radio component designed to introduce active resistance into electrical circuits.
Resistance (often denoted by the letter R or r) is considered, within certain limits, a constant value for a given conductor; it can be calculated as
R = UI >,>
R—resistance, Ohm; U is the electrical potential difference (voltage) at the ends of the conductor, V; I is the current strength flowing between the ends of the conductor under the influence of a potential difference, A.