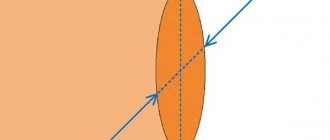
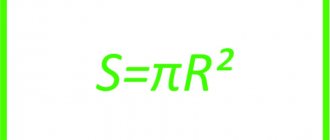A cross section is a figure formed by the intersection of an oblong body with an imaginary plane, located perpendicular to each other, i.e. when the body is cut strictly across its length.
The section can have a simple or complex shape, or be composite.
The area and dimensions (length and width) of the cross section are equal to the corresponding dimensions of this figure.
Our courses to prepare for the Unified State Exam in mathematics, computer science and physics
Courses for those who need to get 90+ and enter a top university in the country.
Mathematics Unified State Exam
Informatics Unified State Exam
Alexey Shevchuk
- course leader and author of the YuKlev textbook (with hundreds of grateful reviews);
- graduated from MIPT, taught at a small physics and technical institute;
- tutoring experience - 18 years;
- in 2022 I passed the Unified State Exam - 100 points (mat, physics) and 98 points (inf);
- rating on Profi.ru - “4.87 out of 5. Very praised. This mark is awarded to experienced specialists with the best reviews.”
Cross-sectional area
In general, the cross-sectional area of a complex or composite shape is defined as the sum (sometimes subtracting) of its constituent simple shapes, such as a rectangle, a triangle, and a circle.
Formulas for calculating the area of the main figures.
Example: Calculate the cross-sectional area of a complex shape with a square hole and a curve. To calculate the total area, a complex section is decomposed into simple figures:
Rectangle - 1, triangle - 2, semicircle - 3 and rectangle - 4, the areas of which are simply determined. As a result, the area of the entire cross-section will be obtained by adding the first three figures and subtracting figure number 4:
A=A1+A2+A3-A4
The cross-sectional area is denoted by the Latin letters S or A , and is measured in square units of length, for example: m2, cm2 or mm2.
Composite sectional area
Composite sections are those that consist of two, three or more separate figures that are not one whole. This could be, for example, a section of a beam, consisting, for example, of a channel and two corners.
These sections themselves are also complex. The cross-sectional areas for such standard profiles can be found in a special reference book - assortment.
As a result, adding up all the component profiles, we obtain the area of the entire cross-section.
Thus, the calculation of the area of the composite section is carried out similarly to the previous procedure, only without subtractions.
Wire cross-section in old buildings and maximum load
In Soviet-era high-rise buildings, aluminum wiring is used. Taking into account the correct connection of the nodes in the junction box, the quality of the insulation and the reliability of the connection contacts, it will last from 10 to 30 years.
If it is necessary to connect equipment with high energy consumption in houses with aluminum wiring, the cross-section and diameter of the cores are selected based on the power consumption. All data is shown in the table.
| Current, A | Maximum power, VA | Cable diameter, mm | Cable cross-section, mm2 |
| 14 | 3000 | 1,6 | 2 |
| 16 | 3500 | 1,8 | 2,5 |
| 18 | 4000 | 2 | 3 |
| 21 | 4600 | 2,3 | 4 |
| 24 | 5300 | 2,5 | 5 |
| 26 | 5700 | 2,7 | 6 |
| 31 | 6800 | 3,2 | 8 |
| 38 | 8400 | 3,6 | 10 |
Maximum current for different thickness of copper wires
Table 1
(Data from table 1.3.4 PUE)
| Cross-section of current-carrying conductor, mm2 | Current, A, for wires laid | ||
| open | in one pipe | ||
| one two core | one three core | ||
| 0,5 | 11 | – | – |
| 0,75 | 15 | – | – |
| 1 | 17 | 15 | 14 |
| 1,2 | 20 | 16 | 14,5 |
| 1,5 | 23 | 18 | 15 |
| 2 | 26 | 23 | 19 |
| 2,5 | 30 | 25 | 21 |
| 3 | 34 | 28 | 24 |
| 4 | 41 | 32 | 27 |
| 5 | 46 | 37 | 31 |
| 6 | 50 | 40 | 34 |
| 8 | 62 | 48 | 43 |
| 10 | 80 | 55 | 50 |
| 16 | 100 | 80 | 70 |
| 25 | 140 | 100 | 85 |
| 35 | 170 | 125 | 100 |
| 50 | 215 | 160 | 135 |
| 70 | 270 | 195 | 175 |
| 95 | 330 | 245 | 215 |
| 120 | 385 | 295 | 250 |
The ratings of wires used in household electrics are highlighted. “One two-core” is a cable with two wires, one of them is Phase, the other is Zero. That is, this is a single-phase load supply. “Single Three-Wire” is for three-phase power supply.
This table shows at what currents and under what conditions a wire of a given cross-section can be operated.
A burning example from practice - if the socket says “Max.16A”, then you can lay a wire with a cross-section of 1.5 mm2 for this one socket . But be sure to protect the outlet with a circuit breaker for a current of no more than 13A, or better yet, 10A. On this topic, you can read my article About replacing and choosing a circuit breaker.
In the table, a single-core wire means that no more wires pass nearby (at a distance of less than 5 wire diameters). Two-core wire - two wires side by side, usually in one common insulation. This is a more severe thermal regime, so the maximum current is less. And the more wires in a cable or bundle, the less the maximum current for each conductor must be due to possible mutual heating.
I find this table not very convenient for practice. After all, most often the initial parameter is the power of the electricity consumer, and not the current, and based on this you need to choose a wire.
How to find the current knowing the power? You need to divide the power P (W) by the voltage (V), and we get the current (A):
I = P/U
How to find power knowing current? You need to multiply current (A) by voltage (V), we get power (W):
P = IU
These formulas are for the case of active load (consumers in residential premises, such as light bulbs and irons). For reactive loads, a factor of 0.7 to 0.9 is usually used (in industry where large transformers and electric motors operate).
I offer you a second table, in which the initial parameters are current consumption and power , and the required values are the wire cross-section and the tripping current of the protective circuit breaker.
Basic Concepts
A triangle is a geometric figure made from three segments. They were connected by three points that did not lie on the same straight line. Segments are usually called sides, and points are called vertices.
Area is a numerical characteristic that gives us information about the size of the part of the plane bounded by a closed geometric figure.
If the values are given in different units of length, we will not be able to know what the area of the triangle will be. Therefore, for a correct solution, it is necessary to convert all data to one unit of measurement.
Popular units for measuring area:
- square millimeter (mm2);
- square centimeter (cm2);
- square decimeter (dm2);
- square meter (m2);
- square kilometer (km2);
- hectare (ha).
Calculation procedure
Since the main task is to find the cross-sectional area of the pipe, the basic formula will be slightly modified.
As a result, the calculations are performed as follows:
S=π×(D/2-N)2, where
D – value of the external section of the pipe;
N – wall thickness.
Please note that the more digits of π you plug into your calculations, the more accurate they will be.
Let us give a numerical example of finding the cross section of a pipe with an outer diameter of 1 meter (N). In this case, the walls have a thickness of 10 mm (D). Without going into details, let's take the number π equal to 3.14.
So the calculations look like this:
S=π×(D/2-N)2=3.14×(1/2-0.01)2=0.754 m2.
Calculation formulas
When carrying out calculations, it must be taken into account that the pipes are essentially cylindrical. Therefore, to find their cross-sectional area, you can use the geometric formula for the area of a circle. Knowing the outer diameter of the pipe and the thickness of its walls, you can find the internal diameter indicator that will be needed for calculations.
The standard formula for the area of a circle is:
S=π×R2, where
π – constant number equal to 3.14;
R – radius value;
S is the cross-sectional area of the pipe, calculated for the internal diameter.
Calculation of wire cross-section for a line of sockets
Cable cross-section for home electrical installations
Each electrical appliance has its own power ratings. They are measured in Watts and indicated in the passport or on a sticker on the case. An example of searching for a cross section would be a power line for a 2.4 kW washing machine. The calculations take into account:
- wire material and installation method - three-core VVGng copper cable hidden in the wall;
- cross-section features - the optimal value is 1.5 mm2, i.e. you will need a 3x1.5 cable;
- using a socket. If only an automatic machine is connected, the characteristics will be sufficient;
- The protection system is an automatic machine with a rated current of 10 A.
For double sockets, a copper cable with a cross-section of 2.5 mm2 and a 16 A circuit breaker are used.
How and with what to measure the diameter of a wire (wire)
To measure the diameter of the wire, a caliper or micrometer of any type (mechanical or electronic) is suitable. It’s easier to work with electronic ones, but not everyone has them. You need to measure the core itself without insulation, so first move it aside or remove a small piece. This can be done if the seller allows it. If not, buy a small piece to test and take measurements on it. On a conductor stripped of insulation, measure the diameter, after which you can determine the actual cross-section of the wire from the found dimensions.
Measuring wire diameter with a micrometer is more accurate than with a mechanical caliper
Which measuring device is better in this case? If we talk about mechanical models, then a micrometer. Its measurement accuracy is higher. If we talk about electronic options, then for our purposes they both give quite reliable results.
If you don't have a caliper or micrometer, take a screwdriver and a ruler with you. You'll have to strip a fairly decent piece of conductor, so you'll hardly be able to do without buying a test sample this time. So, remove the insulation from a 5-10 cm piece of wire. Wind the wire around the cylindrical part of the screwdriver. Lay the coils close to each other, without a gap. All turns must be complete, that is, the “tails” of the wire must stick out in one direction - up or down, for example.
Determining wire diameter using a ruler
The number of turns is not important - about 10. You can have more or less, it’s just easier to divide by 10. Count the turns, then apply the resulting winding to the ruler, aligning the beginning of the first turn with the zero mark (as in the photo). Measure the length of the section occupied by the wire, then divide it by the number of turns. You get the diameter of the wire. It's that simple.
For example, let's calculate the size of the wire shown in the photo above. The number of turns in this case is 11, they occupy 7.5 mm. Divide 7.5 by 11, we get 0.68 mm. This will be the diameter of this wire. Next, you can look for the cross section of this conductor.
For an isosceles triangle
Calculating area using base and height
, where is the base, is the height drawn to the base.
Finding the area through the sides and the angle between them
, where is the side, is the angle between the sides.
Area of an equilateral triangle in terms of the circumradius
, where is the radius of the circumscribed circle.
Area of an equilateral triangle through the radius of the inscribed circle
, where is the radius of the inscribed circle.
Area of an equilateral triangle through a side
, where is the side.
Area of an equilateral triangle through altitude
, where is the height.
Rectangle Information
A rectangle is a quadrangular geometric figure whose opposite sides are equal and the angles are right. A special case of this figure is the square. All its angles are right, and all sides are equal to each other. To perform calculations, you need to know the basic relationships, properties and characteristics.
An important aspect is identifying the figure and applying formulas and relationships to it. In two-dimensional geometry, which is also called Euclidean, you can find an unusual feature that allows you to determine whether a quadrilateral belongs to a rectangle. Its formulation is as follows: at least three angles equal to 90 degrees are sufficient for a quadrilateral to be considered a rectangle.
The statement is easy to prove. This is due to the fact that according to the theorem on the sum of the internal angles of an arbitrary quadrilateral being 360 degrees, the fourth angle is also equal to 90. It is necessary to perform the following calculations to determine the degree measure of the fourth angle: D = 360 - (90 + 90 + 90) = 90. It should be noted that the angles adjacent to them are 90.
Properties and signs
Very often, beginners confuse the properties and characteristics of a figure. However, these are completely different concepts. Signs of a figure are characteristic features that allow it to be classified into one class or another. Properties are a set of axioms that allow the use of certain data in solving or proving theorems and identities. A rectangle has the following characteristics:
- The condition of parallelism and equality of opposite sides.
- The presence of four right angles.
- Equality of diagonals.
- The square of a diagonal is equal to the sum of the squares of two sides that are not opposite.
- All sides are not equal.
It is very important to be able to distinguish geometric shapes. Since a rectangle is a parallelogram, they are often confused. Its main difference is that all angles are equal to 90 degrees. A parallelogram and a rhombus will have angles equal to 90 when they are squares. The latter differs from the desired figure (rectangle) by the equality of all sides. Since a rectangle is a special case of a parallelogram, it has the same properties:
- The angles are equal to 90 degrees.
- Opposite parallel sides are equal.
- The sum of all interior angles is 360.
- A diagonal drawn inside a rectangle divides it into two equal triangles that are equal in size. They are equal according to the third sign of equality of triangles (the dimensions of the sides of one figure are equal to the values of the sides of another figure).
- The triangles obtained by drawing two diagonals are equal in all respects (angles and sides).
- The diagonals intersect each other at a point that divides them into four equal parts.
- The point of intersection of the diagonals is the center of symmetry.
- The sum of the squares of the two diagonals corresponds to the total value of the squares of all sides of the figure.
However, the properties and attributes of a figure are not enough to solve problems. You should know the basic relationships and formulas.
Perimeter and dimension
We need to introduce some notation. Let the sides of the rectangle ABCD be designated by the letters a and b. Since the diagonals are equal, we can only denote the dimension with one letter “d”. The perimeter is the sum of all sides of a given figure. It is denoted by the letter P. To find it, use the following formula: P = 2 * (a + b). However, there is a case when only one side and the diagonal are known. The formula takes the following form: P = 2a + [2 * (2d 2 - 2a 2 )]^(1/2) and P = 2b + [2 * (2d 2 - 2b 2 )]^(1/2).
To calculate the area of a rectangle , you should use the following relationship: S = a * b. This is a basic formula that is also used in the construction industry and physics. However, there is another way in which you can find out the area of a rectangle. It is found using Heron's formula for triangles with areas S1 and S2, and then the result is multiplied by 2. This feature is based on the property of the figure, since the diagonal divides it into two equal triangles.
The relationship is as follows: S = S1 + S2 = 2S1= 2 * ^(1/2). The variable “p” is the semi-perimeter of the triangle. It is found using this method: p = P / 2 = (a + b + d) / 2.