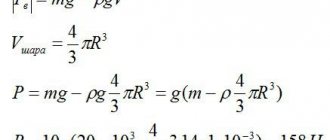Spring pendulum: period and amplitude of oscillation1, formula, rigidity

A spring pendulum is an oscillatory system that consists of a body suspended from a spring. This system is capable of free oscillations.

Such systems are quite widespread due to their functional flexibility. Mechanisms based on such pendulums are often used as elements of automation equipment.

Among other things, they have found application in contact fuses of various ammunition, and as accelerometers in missile control circuits. They are also actively used in safety valves installed in pipelines.

Definitions of a spring pendulum

As previously noted, the spring pendulum has become very widespread. Among the features are the following:

The device is represented by a combination of a load and a spring, the mass of which may not be taken into account. A variety of objects can act as cargo. At the same time, it may be influenced by an external force. A common example is the creation of a safety valve that is installed in a pipeline system. The load is attached to the spring in a variety of ways. In this case, exclusively the classic screw version is used, which is the most widely used. The basic properties largely depend on the type of material used in manufacturing, the diameter of the coil, correct alignment and many other points. The outer turns are often made in such a way that they can withstand a large load during operation.
Before deformation begins, there is no total mechanical energy. In this case, the body is not affected by elastic force. Each spring has an initial position, which it maintains over a long period. However, due to a certain rigidity, the body is fixed in the initial position. It matters how the force is applied. An example is that it should be directed along the axis of the spring, since otherwise there is a possibility of deformation and many other problems. Each spring has its own specific compression and extension limits. In this case, maximum compression is represented by the absence of a gap between individual turns; during tension, there is a moment when irreversible deformation of the product occurs. If the wire is elongated too much, a change in the basic properties occurs, after which the product does not return to its original position.
In the case under consideration, vibrations occur due to the action of elastic force. It is characterized by quite a large number of features that must be taken into account. The effect of elasticity is achieved due to a certain arrangement of turns and the type of material used during manufacture. In this case, the elastic force can act in both directions. Most often, compression occurs, but stretching can also be carried out - it all depends on the characteristics of the particular case.
The speed of movement of a body can vary over a fairly wide range, it all depends on the impact. For example, a spring pendulum can move a suspended load in a horizontal and vertical plane. The effect of the directed force largely depends on the vertical or horizontal installation.

In general, we can say that the definition of a spring pendulum is quite general. In this case, the speed of movement of the object depends on various parameters, for example, the magnitude of the applied force and other moments. Before the actual calculations, a diagram is created:

The support to which the spring is attached is indicated. Often a line with back hatching is drawn to show it.
The spring is shown schematically. It is often represented by a wavy line. In a schematic display, the length and diametrical indicator do not matter.
The body is also depicted. It does not have to match the dimensions, but the location of direct attachment is important.

A diagram is required to schematically show all the forces that influence the device. Only in this case can we take into account everything that affects the speed of movement, inertia and many other aspects.

Spring pendulums are used not only in calculations or solving various problems, but also in practice. However, not all properties of such a mechanism are applicable.

An example is the case when oscillatory movements are not required:

Creation of locking elements.
Spring mechanisms associated with the transportation of various materials and objects.

Calculations of the spring pendulum allow you to select the most suitable body weight, as well as the type of spring. It is characterized by the following features:

Diameter of turns. It can be very different. The diameter largely determines how much material is required for production. The diameter of the coils also determines how much force must be applied to achieve full compression or partial extension. However, increasing the size can create significant difficulties with the installation of the product.
The diameter of the wire. Another important parameter is the diametrical size of the wire. It can vary over a wide range, depending on the strength and degree of elasticity.
Length of the product. This indicator determines how much force is required for complete compression, as well as what elasticity the product can have.
The type of material used also determines the basic properties. Most often, the spring is made using a special alloy that has the appropriate properties.

In mathematical calculations, many points are not taken into account. The elastic force and many other indicators are determined by calculation.

Types of spring pendulum

There are several different types of spring pendulum. It is worth considering that classification can be carried out according to the type of spring installed. Among the features we note:

Vertical vibrations have become quite widespread, since in this case there is no frictional force or other influence on the load. When the load is positioned vertically, the degree of influence of gravity increases significantly. This execution option is common when carrying out a wide variety of calculations. Due to the force of gravity, there is a possibility that the body at the starting point will perform a large number of inertial movements. This is also facilitated by the elasticity and inertia of the body at the end of the stroke.
A horizontal spring pendulum is also used. In this case, the load is on the supporting surface and friction also occurs at the time of movement. When positioned horizontally, gravity works somewhat differently. The horizontal position of the body has become widespread in various tasks.

The movement of a spring pendulum can be calculated using a sufficiently large number of different formulas, which must take into account the influence of all forces. In most cases, a classic spring is installed. Among the features we note the following:

The classic coiled compression spring has become very widespread today. In this case, there is a space between the turns, which is called a pitch. The compression spring can stretch, but often it is not installed for this. A distinctive feature is that the last turns are made in the form of a plane, which ensures uniform distribution of force.
A stretch version can be installed. It is designed for installation in cases where the applied force causes an increase in length. For fastening, hooks are placed.

Both options are common. It is important to ensure that the force is applied parallel to the axis. Otherwise, there is a possibility of displacement of the turns, which causes serious problems, for example, deformation.

Elastic force in a spring pendulum

It should be taken into account that before the spring is deformed, it is in an equilibrium position. The applied force can cause it to stretch and compress. The elastic force in a spring pendulum is calculated in accordance with how the law of conservation of energy operates. According to accepted standards, the resulting elasticity is proportional to the displacement of the body. In this case, the kinetic energy is calculated using the formula: F=-kx. In this case, the spring constant is used.

There are quite a large number of features of the influence of the elastic force in a spring pendulum. Among the features we note:

The maximum elastic force occurs at the moment when the body is at the maximum distance from the equilibrium position. At the same time, in this position the maximum value of the acceleration of the body is noted. We should not forget that the spring can be stretched or compressed; both options are somewhat different. When compressed, the minimum length of the product is limited. As a rule, it has a length equal to the diameter of the coil multiplied by the number. Too much force can cause the turns to shift, as well as deformation of the wire. When stretching, there is a moment of elongation, after which deformation occurs. Strong elongation leads to the fact that the resulting elastic force is not enough to return the product to its original state.
As the body approaches the point of equilibrium, a significant decrease in the length of the spring occurs. Due to this, a constant decrease in the acceleration rate is observed. All this occurs due to the influence of elastic force, which is associated with the type of material used in the manufacture of the spring and its characteristics. The length decreases due to the fact that the distance between the turns is reduced. A feature can be called the uniform distribution of turns, only in the case of defects there is a possibility of violating such a rule.
When the equilibrium point is reached, the elastic force decreases to zero. However, the speed does not decrease, since the body moves by inertia. The equilibrium point is characterized by the fact that the length of the product in it is maintained over a long period, provided there is no external deforming force. The equilibrium point is determined in the case of constructing a diagram.
After reaching the equilibrium point, the resulting elasticity begins to reduce the speed of movement of the body. It works in the opposite direction. In this case, a force arises that is directed in the opposite direction.
Having reached the extreme point, the body begins to move in the opposite direction. Depending on the stiffness of the installed spring, this action will be repeated several times. The length of this cycle depends on a variety of factors. An example is body weight, as well as the maximum applied force to cause deformation. In some cases, the oscillatory movements are almost imperceptible, but they still occur.

The above information indicates that the oscillatory movements are accomplished due to the effects of elasticity. Deformation occurs due to the applied force, which can vary over a fairly large range, it all depends on the specific case.

Harmonic vibrations.

We will assume that the position of the oscillating body is determined by a single coordinate.
The equilibrium position corresponds to the value . The main task of mechanics in this case is to find a function that gives the coordinate of the body at any time. For a mathematical description of oscillations, it is natural to use periodic functions. There are many such functions, but two of them - sine and cosine - are the most important. They have many good properties and are closely related to a wide range of physical phenomena.

Since the sine and cosine functions are obtained from each other by shifting the argument by , we can limit ourselves to only one of them. For definiteness, we will use cosine.

Harmonic oscillations are oscillations in which the coordinate depends on time according to the harmonic law:

(1)

Let us find out the meaning of the quantities included in this formula.

A positive value is the largest modulus value of the coordinate (since the maximum value of the cosine modulus is equal to unity), i.e., the largest deviation from the equilibrium position. Therefore - the amplitude of oscillations.

The cosine argument is called the phase of oscillation. The value equal to the phase value at is called the initial phase. The initial phase corresponds to the initial coordinate of the body: .

The quantity is called cyclic frequency. Let's find its connection with the oscillation period and frequency. One complete oscillation corresponds to a phase increment equal to radians: , whence

(2)

(3)

The cyclic frequency is measured in rad/s (radians per second).

In accordance with expressions (2) and (3), we obtain two more forms of writing the harmonic law (1):

The graph of function (1), expressing the dependence of the coordinate on time during harmonic oscillations, is shown in Fig. 1.

Rice. 1. Harmonic graph

The harmonic law of type (1) is of the most general nature. It responds, for example, to situations where two initial actions were simultaneously performed on the pendulum: it was deflected by an amount and a certain initial speed was given to it. There are two important special cases when one of these actions was not performed.

Let the pendulum be deflected, but the initial speed was not reported (it was released without the initial speed). It is clear that in this case , therefore we can put . We get the cosine law:

The graph of harmonic oscillations in this case is shown in Fig. 2.

Rice. 2. Law of cosine

Let us now assume that the pendulum was not deflected, but the initial velocity from the equilibrium position was imparted to it by impact. In this case, so you can put . We get the law of sine:

The oscillation graph is shown in Fig. 3.

Rice. 3. Law of sine

Equations of oscillations of a spring pendulum

The spring pendulum oscillates according to the harmonic law. The formula used for the calculation is as follows: F(t)=ma(t)=-mw2x(t).

The above formula gives (w) the radial frequency of the harmonic vibration. It is characteristic of a force that extends within the limits of applicability of Hooke's law. The equation of motion can differ significantly, it all depends on the specific case.

If we consider oscillatory motion, we should pay attention to the following points:

Oscillatory movements are observed only at the end of the body's movement. Initially it is straight until the force is completely released. In this case, the elastic force is maintained throughout the entire time the body is in the most distant position from the zero coordinates.
After stretching, the body returns to its original position. The resulting inertia becomes the reason why the spring may be affected. Inertia largely depends on body weight, developed speed and many other factors.

The result is an oscillation that can last for a long period. The above formula allows you to carry out a calculation taking into account all the points.

Equation of harmonic vibrations.

Let's return to the general harmonic law (1). Let's differentiate this equality:
. (4)

Now we differentiate the resulting equality (4):

. (5)

Let's compare expression (1) for the coordinate and expression (5) for the acceleration projection. We see that the acceleration projection differs from the coordinate only by a factor:

. (6)

This relationship is called the harmonic vibration equation. It can also be rewritten in this form:

. (7)

From a mathematical point of view, equation (7) is a differential equation. The solutions to differential equations are functions (not numbers, as in ordinary algebra). So, it can be proven that:

-the solution to equation (7) is any function of the form (1) with arbitrary ;

-no other function is a solution to this equation.

In other words, relations (6), (7) describe harmonic oscillations with a cyclic frequency and only them. Two constants are determined from the initial conditions - from the initial values of the coordinate and velocity.

Formulas for the period and frequency of oscillation of a spring pendulum

When designing and calculating the main indicators, quite a lot of attention is also paid to the frequency and period of oscillation. Cosine is a periodic function that uses a value that does not change after a certain period of time. This indicator is called the period of oscillation of a spring pendulum. The letter T is used to denote this indicator; the concept characterizing the value inverse to the oscillation period (v) is also often used. In most cases, the formula T=1/v is used in calculations.

The period of oscillation is calculated using a somewhat complicated formula. It is as follows: T=2п√m/k. To determine the oscillation frequency, the formula is used: v=1/2п√k/m.

The considered cyclic frequency of oscillation of a spring pendulum depends on the following points:

The mass of a load that is attached to a spring. This indicator is considered the most important, as it affects a variety of parameters. The force of inertia, speed and many other indicators depend on the mass. In addition, the mass of the cargo is a quantity whose measurement does not pose any problems due to the presence of special measuring equipment.
Elasticity coefficient. For each spring this indicator is significantly different. The elasticity coefficient is indicated to determine the main parameters of the spring. This parameter depends on the number of turns, the length of the product, the distance between the turns, their diameter and much more. It is determined in a variety of ways, often using special equipment.

Do not forget that when the spring is strongly stretched, Hooke's law ceases to apply. In this case, the period of spring oscillation begins to depend on the amplitude.

The universal time unit, in most cases seconds, is used to measure the period. In most cases, the amplitude of oscillations is calculated when solving a variety of problems. To simplify the process, a simplified diagram is constructed that displays the main forces.

Spring and mathematical pendulums

Newton's second law (fundamental law of dynamics): the acceleration acquired by a material point is directly proportional to the resultant of all forces acting on it, and inversely proportional to the mass of the material point:

Hooke's law: the modulus of the elastic force arising in a body during elastic deformations is directly proportional to its absolute elongation (compression):

where k is the rigidity of the body, is the length of the undeformed body, l is the length of the deformed body.

Let's consider a spring pendulum , which is an oscillatory system formed by a load on a spring.

Let a load of mass m lying on a smooth horizontal surface be attached to the free end of a weightless spring with stiffness k (Fig. 3). The second end of the spring is fixed relative to a given inertial reference system (IRS).

Let us remove the load from the equilibrium position by moving it a distance x to the right. An elastic force directed to the left will arise in the spring.

Let's write down Newton's second law for the movement of a load:

In the projection onto the Ox axis of the forces acting on the load, taking into account Hooke’s law, we obtain

Hence,

This equation is similar to the equation of harmonic vibrations

Comparing these two equations, we find the cyclic frequency of oscillation of the spring pendulum:

Then the period of oscillation of the spring pendulum can be found using the formula

As follows from the formula obtained, the period of oscillation of a spring pendulum does not depend on the amplitude of its oscillations (within the limits of the feasibility of Hooke’s law).

The property of independence of the period of oscillation of a pendulum from the amplitude is called isochronism (from the Greek words - equal and - time). Thus, the oscillations of a spring pendulum have the property of isochronism.

The isochronism of pendulum oscillations was discovered by Galileo Galilei in 1583 while studying the motion of a weight suspended on a thread. The model of this oscillatory system is a mathematical pendulum.

A mathematical pendulum is a material point of mass m suspended on a weightless inextensible thread of length l in a field of any forces, for example, the force of gravity of the Earth (Fig. 4).

A mathematical pendulum is an idealized model of a real pendulum, provided that the length of the thread is much greater than the size of the body suspended on it and the mass of the thread is much less than the mass of the body. In addition, the deformation of the thread can be neglected.

Galileo Galilei experimentally determined that the period of small oscillations (9). He also established that the period of these oscillations is directly proportional to .

The period of small oscillations of a mathematical pendulum in the Earth's gravity field is determined by Huygens' formula:

At a deflection angle of a mathematical pendulum of 20°, the error in calculating the period of oscillation of a mathematical pendulum using the Huygens formula does not exceed 1%.

The deviation of the pendulum from the equilibrium position will be characterized by the angle (see Fig. 4) that the thread forms with the vertical.

According to Newton's second law for the motion of the ball, we can write:

The displacement of the pendulum along the arc x = l, where the angle is expressed in radians. The restoring force in this case is the projection of gravity onto the tangent to the arc (see Fig. 4), which is determined by the formula:

Note that at small angles and the arc length

differs very little from the chord length. For small angles (up to 10°), the values of and sin differ by less than I%. Therefore, for such angles the equality

(1)

is a very good approximation.

Substituting the value into expression (1), we get

Thus, the equation of motion of the pendulum will be written in the form

Since the resulting equation coincides with the equation of harmonic oscillations, we can conclude that for small deviations the pendulum performs harmonic oscillations with a cyclic frequency

As can be seen from this formula, the cyclic frequency does not depend on the mass of the pendulum and the amplitude of its oscillations, but is determined only by its length and the acceleration of gravity.

In the general case, when the pendulum is in uniform fields of several forces, to determine the period of oscillation, one should introduce “effective acceleration”, which characterizes the resulting action of these fields, and the period of oscillation of the pendulum will be determined by the formula

Example:

Determine the amplitude A, cyclic frequency , period T and the initial phase of oscillation of a body of mass m = 0.50 kg suspended from a vertical spring (Fig. 5). It is known that at rest the body stretches the spring by = 10 mm and to excite oscillations it is shifted down by x = 30 mm and released.

Solution

The cyclic frequency of oscillations of a “vertical” spring pendulum is also determined by the formula

Let's find the spring stiffness k. From the condition of body equilibrium it follows

According to Hooke's law

In the projection onto the Ox axis, the equilibrium condition will be written as:

From here we get for the cyclic frequency

Since, according to the conditions of the problem, the body was displaced at a distance x = 30 mm from the equilibrium position, then the amplitude of its oscillations

The oscillation period is found from the relation

Since at the initial moment of time the body was displaced by the maximum amount, then the initial phase of oscillations Answer :

Example:

A metal ball suspended on a long, light, inextensible thread is raised vertically to the point of suspension and released. Then the pendulum thread is deflected at a small angle from the vertical and also released. In which of these cases will the ball return to its initial position faster?

Solution

In the first case, the ball falls freely without an initial speed from a height h = l, therefore,

From here we find the time period required to return the ball to its initial position:

In the second case, the time interval required for the ball to return from the deflected position to the equilibrium position will be found from the equation of harmonic oscillations

Since at the initial moment t = 0 the pendulum has a maximum

deviation from the equilibrium position, then the initial phase of oscillations Since in the equilibrium position x = 0, then

Using the formula for the period of oscillation of a mathematical pendulum

we find

Dividing the equations for time intervals term by term we get

Answer : the ball will return to its initial position faster when it moves vertically downward.

Example:

Find the periods of oscillation of a mathematical pendulum with length l = 1.0 m when its suspension point moves with acceleration, the modulus of which is a = , directed: a) vertically upward; b) vertically down.

Solution

Period of oscillation of a mathematical pendulum in the Earth's gravity field

a) When the pendulum moves with acceleration directed upward (Fig. 6, a), the equation of motion along the Oy axis

where Fy is the projection of the elastic force of the thread. Where do we find it from?

where g* = g + a - “effective acceleration”. The period of oscillation is determined by the formula

b) When the pendulum suspension point moves with acceleration directed downward (Fig. 6, b), the equation of motion along the Oy axis

where Fy is the projection of the elastic force of the thread. Where do we find it from?

where g*=ga is “effective acceleration”. Oscillation period

Answer:

What are spring and mathematical pendulums?

Newton's second law (basic law of dynamics): the acceleration of a body is directly proportional to the resultant force and inversely proportional to the mass of the body:

Hooke's law: during elastic deformations of compression and tension, the modulus of the elastic force is directly proportional to the modulus of change in the length of the body:

where is the rigidity of the body, is the length of the undeformed body, is the length of the deformed body.

An oscillatory system consisting of a body with a spring attached to it is called a spring pendulum. The spring can be positioned either vertically (vertical spring pendulum) or horizontally (horizontal spring pendulum).

Let us consider the oscillations of a horizontal spring pendulum. Let a mass of mass lying on a smooth horizontal surface be attached to the free end of a light (weightless) spring with rigidity (Fig. 6). The second end of the spring is motionless relative to the given inertial reference system (IRS).

Let's remove the load from the equilibrium position by moving it a distance to the right (see Fig. 6). Then an elastic force will arise in the spring acting on the load and directed to the left.

According to Newton's second law for the movement of cargo

In the projection onto the axis of the forces acting on the load (see Fig. 6), taking into account Hooke’s law, we obtain:

Let us rewrite the resulting relationship as:

which is the equation of harmonic oscillations of a spring pendulum.

Comparing (1) with the equation of harmonic oscillations we find the cyclic frequency of oscillations of the horizontal spring pendulum

which is determined by the mass of the load and the spring stiffness.

To find the period of oscillation of a spring pendulum, we use the formula, substituting expression (2) into it: As follows from formulas (2) and (3), the period and frequency of oscillation of a spring pendulum do not depend on the amplitude of its oscillations (within the feasibility of Hooke’s law).

The property of independence of the period of oscillation of a pendulum from the amplitude is called isochronism (from the Greek (isos) - equal and (chronos) - time). Consequently, the oscillations of a spring pendulum have the property of isochronism.

An oscillatory system consisting of a body located in a gravitational field, suspended on a light inextensible thread, the dimensions of which are small compared to the length of the thread, and its mass is significantly greater than the mass of the thread, is called a mathematical pendulum. Under such conditions, the body can be considered a material point, and the thread can be considered a light, inextensible one (Fig. 7).

Let's consider the oscillations of a mathematical pendulum.

The deviation of the pendulum from the equilibrium position will be characterized by the angle (see Fig. 7) that the thread forms with the vertical.

After the pendulum is deflected, two forces act on it: the gravity force directed vertically downward and the elastic force directed along the thread. Under the influence of these forces, the body moves along a circular arc to a stable equilibrium position.

According to Newton's second law, we can write for the motion of a pendulum:

In projections onto the selected coordinate axes (see Fig. 7) we obtain:

For deviation angles, the values differ by less than 1%. Therefore, at small angles of deflection, the length of the arc differs very little from the length of the chord where the angle is expressed in radians. Then the displacement of the pendulum along the arc But practically the pendulum moves along the I axis is found and, substituting this expression in (5), we obtain:

Thus, the force that returns the pendulum to a stable equilibrium position is the elastic force of its thread.

At small angles of deflection of the pendulum, the projection of the acceleration vector can be neglected, and then from equation (6) it follows that

Consequently, the equation of motion of the pendulum along the axis will be written in the form:

where is the acceleration imparted to the pendulum bob by the elastic force of the thread.

From here we obtain the equation of harmonic oscillations of a mathematical pendulum:

When comparing equation (8) with the equation of harmonic oscillations, we can conclude that for small deviations the mathematical pendulum performs harmonic oscillations with a cyclic frequency

Then the period of small oscillations of a mathematical pendulum in the Earth’s gravitational field is determined by Huygens’ formula:

which was first received by I. Newton’s student Christiaan Huygens.

At the angles of deflection of a mathematical pendulum, the error in calculating the period of oscillation of a mathematical pendulum according to the Huygens formula does not exceed 1%.

As can be seen from formulas (9) and (10), the cyclic frequency and period of a mathematical pendulum do not depend on the mass of the pendulum and the amplitude of its oscillations, but are determined only by its length and the magnitude of the acceleration of free fall

Galileo Galilei was the first to experimentally determine that the period of small oscillations of a mathematical pendulum with a length in a gravity field does not depend on its mass and amplitude of oscillations (the angle of initial deflection). He also established that the period of these oscillations is directly proportional

If the pendulum acquires additional acceleration due, for example, to the accelerated movement of the suspension point, then the elastic force of the thread will change. In this case, the period of oscillation of the pendulum will be determined by the formula:

where is the “effective acceleration” equal to the vector difference

Order solutions to physics problems

Example:

Derive a formula for the period of oscillation of a vertical spring pendulum if the mass of the load and the spring stiffness

Solution

Let us consider the vertical movement of the load, which occurs under the action of the elastic force of the spring and the force of gravity of the load after a push. Let us place the origin of coordinates at the point corresponding to the equilibrium position of the body (Fig. 8). In this position, the spring is stretched by an amount determined by the relationship:

When the load is displaced by an amount from the equilibrium position, the force acting on the load from the spring is equal to

Then according to Newton's second law

Taking into account relation (1), we rewrite this equation in the form:

If you enter the notation, the equation of motion of the load will be written in the form:

It describes the harmonic oscillations of a vertical spring pendulum with a frequency the same as that of a horizontal spring pendulum. Consequently, the period of oscillation of a vertical spring pendulum is the same as that of a horizontal one:

Answer:

Thus, the constant force acting in the oscillatory system only shifts the equilibrium positions, but does not change the frequency of oscillations.

Example:

Determine the amplitude, cyclic frequency, period and initial phase of oscillations of a body of mass g suspended from a vertical spring (Fig. 9). It is known that in a state of rest, a body stretches a spring by a distance of mm and to excite oscillations it is shifted downwards by a distance of mm from the equilibrium position and released.

Given:

Solution

The cyclic frequency of oscillation of a vertical spring pendulum, as well as a horizontal one, is determined by the formula (see example 1):

To find the spring stiffness k, we write down the equilibrium condition of the body:

According to Hooke's law

In the projection onto the axis, the equilibrium condition will be written:

From here we get for the cyclic frequency:

The amplitude of the pendulum's oscillations is determined by the initial mixing:

The period of oscillation is found from the relation:

Since at the initial moment of time the body was displaced by the maximum amount, then the initial phase of oscillations

Answer:

Formulas for the amplitude and initial phase of a spring pendulum

Having decided on the features of the processes involved and knowing the equation of oscillation of the spring pendulum, as well as the initial values, you can calculate the amplitude and initial phase of the spring pendulum. The value of f is used to determine the initial phase, and the amplitude is indicated by the symbol A.

To determine the amplitude, the formula can be used: A=√x2+v2/w2. The initial phase is calculated using the formula: tgf=-v/xw.

Using these formulas, you can determine the main parameters that are used in the calculations.

Vibration energy of a spring pendulum

When considering the oscillation of a load on a spring, one must take into account the fact that the movement of the pendulum can be described by two points, that is, it is rectilinear in nature. This moment determines the fulfillment of the conditions relating to the force in question. We can say that the total energy is potential.

It is possible to calculate the oscillation energy of a spring pendulum by taking into account all the features. The main points are the following:

Oscillations can take place in the horizontal and vertical plane.
Zero potential energy is chosen as the equilibrium position. It is in this place that the origin of coordinates is established. As a rule, in this position the spring retains its shape provided there is no deforming force.
In the case under consideration, the calculated energy of the spring pendulum does not take into account the friction force. When the load is vertical, the friction force is insignificant; when the load is horizontal, the body is on the surface and friction may occur during movement.
To calculate the vibration energy, the following formula is used: E=-dF/dx.

The above information indicates that the law of conservation of energy is as follows: mx2/2+mw2x2/2=const. The formula used says the following:

The maximum kinetic energy of the installed pendulum is directly proportional to the maximum potential value.
At the moment of the oscillator, the average value of both forces is equal.

It is possible to determine the oscillation energy of a spring pendulum when solving a variety of problems.

Examples of problems with solutions

Exercise. The period of oscillation of a spring pendulum is $T=5cdot <10>^<-3>s$. What is the oscillation frequency in this case? What is the cyclic frequency of vibration of this mass?

Solution. The oscillation frequency is the reciprocal of the oscillation period, therefore, to solve the problem it is enough to use the formula:

Let's calculate the required frequency:

The cyclic frequency is related to the frequency $u$ as:

Let's calculate the cyclic frequency:

[_0=2pi cdot 200approx 1256 left(frac<rad><с> ight).]

Answer. $1) u =200$ Hz. 2) $_0=1256 frac<rad><s>$

Exercise. The mass of the load hanging on an elastic spring (Fig. 2) is increased by $Delta m$, while the frequency decreases by $n$ times. What is the mass of the first load?

Solution. We will assume that the loads on the spring perform free harmonic oscillations, then we will take the formula as the basis for solving the problem:

For the first load the frequency will be equal to:

For the second load:

Let us obtain from equation (2.3) the required mass of the load. To do this, let’s square both sides of expression (2.3) and express $m$:

The author is a professional tutor, author of textbooks for preparing for the Unified State Exam Igor Vyacheslavovich Yakovlev

Topics of the Unified State Examination codifier: harmonic vibrations; amplitude, period, frequency, phase of oscillations; free vibrations, forced vibrations, resonance.

Oscillations are changes in the state of a system that repeat over time. The concept of oscillations covers a very wide range of phenomena.

Oscillations of mechanical systems, or mechanical vibrations, are the mechanical movement of a body or system of bodies, which is repeatable in time and occurs in the vicinity of the equilibrium position. An equilibrium position is a state of a system in which it can remain indefinitely without experiencing external influences.

For example, if the pendulum is deflected and released, it will begin to oscillate. The equilibrium position is the position of the pendulum in the absence of deviation. The pendulum, if left undisturbed, can remain in this position for as long as desired. As the pendulum oscillates, it passes through its equilibrium position many times.

Immediately after the deflected pendulum was released, it began to move, passed the equilibrium position, reached the opposite extreme position, stopped there for a moment, moved in the opposite direction, passed the equilibrium position again and returned back. One complete oscillation took place. Then this process will be repeated periodically.

The amplitude of a body’s oscillations is the magnitude of its greatest deviation from the equilibrium position.

The period of oscillation is the time of one complete oscillation. We can say that during a period the body travels a path of four amplitudes.

The oscillation frequency is the reciprocal of the period: . Frequency is measured in hertz (Hz) and shows how many complete oscillations occur in one second.

Free oscillations of a spring pendulum

When considering what causes the free vibrations of a spring pendulum, attention should be paid to the action of internal forces. They begin to form almost immediately after movement has been transferred to the body. Features of harmonic oscillations include the following points:

Other types of forces of an influencing nature may also arise, which satisfy all the norms of the law, called quasi-elastic.
The main reasons for the action of the law may be internal forces that are formed immediately at the moment of a change in the position of the body in space. In this case, the load has a certain mass, the force is created by fixing one end to a stationary object with sufficient strength, the second to the load itself. In the absence of friction, the body can perform oscillatory movements. In this case, the fixed load is called linear.

We should not forget that there are simply a huge number of different types of systems in which oscillatory motion occurs. Elastic deformation also occurs in them, which becomes the reason for their use for performing any work.