Mechanical properties, deformation and recrystallization of metals.

Mechanical properties of materials

Mechanical properties characterize the ability of materials to resist external forces. The main mechanical properties include strength, hardness, impact strength, elasticity, ductility, brittleness, etc.

Strength is the ability of a material to resist the destructive effects of external forces.

Hardness is the ability of a material to resist the penetration of another, harder body into it under load.

Viscosity is the property of a material to resist destruction under dynamic loads.

Elasticity is the property of materials to restore their size and shape after the load is removed.

Plasticity is the ability of materials to change their size and shape under the influence of external forces without collapsing.

Fragility is the property of materials to collapse under the influence of external forces without residual deformation.

In static tensile tests, values ​​characterizing the strength, ductility and elasticity of the material are determined. Tests are carried out on cylindrical (or flat) samples with a certain ratio between length l0 and diameter d0. The sample is stretched under the action of the applied force P (Fig. 1, a) until destruction. An external load causes stress and deformation in the sample. Stress σ is the ratio of force P to cross-sectional area F0, MPa:

σ = P/F0,

Deformation characterizes the change in sample dimensions under load, %:

ε = [(l1-l0)/l0] 100,

where l1 is the length of the stretched sample.

Deformation can be elastic (disappearing after the load is removed) or plastic (remaining after the load is removed).

During testing, a tensile diagram is drawn, which represents the dependence of stress on deformation. In Fig. 1 shows such a diagram for low-carbon steel. After testing, the following characteristics of mechanical properties are determined.

The elastic limit σу is the maximum stress at which plastic deformation does not occur in the sample.

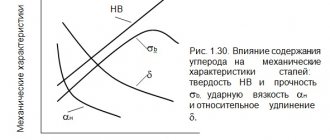
The yield strength σт is the stress corresponding to the yield area on the tensile diagram (Fig. 1). If there is no yield plateau on the diagram (which is observed for brittle materials), then the conditional yield strength σ0.2 is determined - the stress causing plastic deformation equal to 0.2%. Ultimate strength (or temporary resistance) σв is the stress corresponding to the maximum load that the sample can withstand during testing.

Relative elongation after rupture δ is the ratio of the increment in length of the sample during tension to the initial length l0, %:

δ = [(lk-l0)/l0] 100,

where lк is the length of the sample after rupture.

Rice. 1. Static tensile tests: a – test diagram;

b – tension diagram

Relative narrowing after rupture ψ is the decrease in the cross-sectional area of ​​the sample, related to the initial cross-section of the sample, %:

ψ = [(F0-Fk)/F0] 100,

where Fк is the cross-sectional area of ​​the sample at the fracture site. Relative elongation and relative contraction characterize the plasticity of the material.

The hardness of metals is measured by pressing a hard tip of various shapes into the test sample.

The Brinell method is based on pressing a hardened steel ball into the metal surface under a certain load. After the load is removed, an imprint remains in the sample. The Brinell hardness number HB is determined by the ratio of the load acting on the ball to the surface area of ​​the resulting print.

The Rockwell method is based on pressing a hardened steel ball with a diameter of 1.588 mm (scale B) or a diamond cone with an apex angle of 120° (scales A and C) into the test sample. Indentation is carried out under the action of two loads - preliminary equal to 100 N and final equal to 600, 1000. 1500 N for scales A, B and C, respectively. The Rockwell hardness number HRA, HRB and HRC is determined by the difference in indentation depths.

The Vickers method uses indentation of a diamond tetrahedral pyramid with an apex angle of 136°. The Vickers hardness number HV is determined by the ratio of the applied load to the surface area of ​​the indentation.

Impact strength is determined by the work A spent on the destruction of the sample, divided by its cross-sectional area F; J/m2:

KC = A/F

Tests are carried out by hitting a special pendulum pile driver. For testing, a standard notched sample is used, mounted on the supports of the pile driver. A pendulum of a certain mass strikes the side opposite the cut.

The concept of structural strength of materials and criteria for its assessment

Factors that determine the performance of structural materials:

• static, cyclic and shock loads;
• low and high temperatures;
• contact with various environments.

These factors determine the requirements for structural materials, the main of which are operational, technological, and economic.

Performance requirements are of paramount importance. In order to ensure the functionality of specific machines and devices, the structural material must have high structural strength.

Structural strength is a set of mechanical properties that ensure reliable and long-term operation of a material under operating conditions.

It must be remembered that the required characteristics of the mechanical properties of a material for a particular product depend not only on force factors, but also on the impact of the working environment and temperature on it.

The working environment - liquid, gaseous, ionized, radiation, as a rule, has a negative effect on the mechanical properties of the material (corrosion cracking, oxidation, changes in the chemical composition and, as a result, embrittlement, etc.)

Temperature range from -269 to 2000°C. The material is required to have heat resistance, and at low temperatures, cold resistance.

Technological requirements are aimed at ensuring the least labor intensive manufacturing of parts and structures. The manufacturability of a material characterizes the possible methods of its processing. It is assessed by: machinability, pressure, weldability, castability, hardenability, tendency to deformation and warping during heat treatment. The performance and manufacturing quality of the part depend on it.

Economic requirements boil down to ensuring that the material is low cost and accessible. The use of materials containing alloying elements (especially scarce ones) must be justified by increasing the performance properties of the part. These requirements become especially important when production is on a mass scale.

Structural strength is a complex characteristic that includes a combination of criteria:

• strength;
• reliability;
• durability.

The strength criteria of the material are selected depending on its operating conditions.

Under static loads, during tensile testing, tensile strength ( σв) or yield strength ( σ0.2, σт ) characterize the material’s resistance to plastic deformation (Fig. 1). For an approximate assessment of static strength, hardness HB or HR is used (Fig. 2, 3) (for steel, the empirical relation σв = HB/3 ).

Fig.1 Tensile test

Fig.2 Brinell hardness measurement

Under cyclic loads: endurance limit σR (with symmetrical circular bending σ-1 ).

It must be remembered that the greater the strength of the material, the greater the permissible operating stresses and thus the smaller the size and weight of the part.

However, an increase in the level of material strength and, as a consequence, operating stresses is accompanied by an increase in elastic deformations:

εcontrol = σcontrol/E,

where E is the modulus of normal elasticity (Young’s modulus), a characteristic of the rigidity of the metal. It is the criteria of rigidity, and not strength, that determine the dimensions of machine tool beds, gearbox housings and other parts that are required to maintain exact dimensions and shape.

The opposite requirement is also possible. For springs, membranes and other sensitive elastic elements of devices, it is important to ensure large elastic movements. Then the material is required to have a high elastic limit σel and a low elastic modulus E.

Fig.3 Rockwell hardness measurement

Addition: For materials used in aircraft and rocketry, the mass efficiency of the material is important. It is assessed by specific characteristics:

• specific strength σв/ρg ( ρ – density, g – accelerated free fall);
• specific hardness E/ ρg .

Note: To evaluate structural strength, strength characteristics at operating temperatures and operating environments are required.

Conclusion - as criteria for structural strength, those characteristics are selected that most fully reflect the strength under specific operating conditions.

Reliability is the property of a material to resist brittle fracture (sudden failure).

To prevent brittle fracture, structural materials must have:

• sufficient plasticity δ, % and ψ , %;
• impact strength KCU ( MJ/m2 ) Fig.4, Fig.5

Rice. 4 Pendulum pile driver for determining impact strength

Fig.5 Impact tests

However, these parameters were determined on laboratory samples, without taking into account the actual operating conditions of a particular part. It is necessary to take into account that under operating conditions there are factors that further reduce their ductility and toughness and increase the risk of brittle fracture:

• stress concentrators (notches);
• temperature drop;
• dynamic loads;
• increasing the size of parts (scale factor).

In order to avoid sudden failures under operating conditions, it is necessary to take into account crack resistance.

Crack resistance is a group of reliability parameters that characterize the ability of a material to inhibit the development of a crack.

Cracks are sharp stress concentrators, local stresses at the tip of which can be many times higher than the average design stresses.

For a crack of length l and radius r, stresses at the tip:

σумах = σср 2 √ l/ r

The longer the crack and the sharper its tip, the greater the stress concentration. For plastic materials, the danger of such defects is not great. Brittle materials, on the other hand, are extremely sensitive to cuts.

The reliability of high-strength materials is assessed by the size of the permissible defect (crack) using the J. Irwin criterion (K ) .

К = σср √ α π lкр , (MPa x mm1/2)

where π is a dimensionless coefficient characterizing the geometry of the crack.

K – criterion of fracture toughness, depends on the degree of plastic deformation at the tip of the crack (its bluntness) and characterizes the development of a ductile crack. The larger it is, the higher the reliability of the material.

To assess the reliability of a material, the following parameters are also used:

• impact strength KSU, KSV, KST (MJ/m2);
• cold brittleness temperature threshold T50.

parameter evaluates the suitability of a material for pressure vessels, pipelines and other high-reliability structures.

parameter , determined on samples with a fatigue crack at the base of the notch, is more indicative. It is taken into account when choosing materials for structures of especially critical use (aircraft, turbine rotors).

The cold brittleness threshold T50 characterizes the effect of a decrease in temperature on the susceptibility of a material to brittle fracture. It is determined based on the results of impact tests of notched samples at decreasing temperature (Fig. 6). T50 - indicates the temperature at which the fracture of the sample contains 50% of the fibrous component, and the value of the CST is reduced by half.

Fig.6 Temperature Tchl. (T50) cold brittleness threshold

Durability is the property of a material to resist the development of gradual destruction (gradual failure), ensuring the performance of parts for a given time (resource).

Gradual failure is a loss of performance by a material, upon which the parts are replaced without the threat of emergency consequences.

Causes of loss of performance, i.e. gradual withdrawal:

• development of fatigue processes;
• wear;
• creep;
• corrosion;
• radiation swelling, etc.

These processes cause the gradual accumulation of irreversible damage in the material and its destruction. Ensuring the durability of a material means reducing the rate of its destruction to the required values.

For most machine parts (more than 80%), durability is determined by the material's resistance to fatigue failure (cyclic durability) or wear resistance (wear resistance).

Cyclic durability characterizes the performance of a material under conditions of repeated stress cycles. Voltage cycle is a set of changes in voltage between its two limiting values ​​σ max and σ min during the period T.

The sinusoidal cycle of voltage change is characterized by the cycle asymmetry coefficient R = σ min / σ max; voltage amplitude σ a = (σ max σ min ) /2 ; average cycle voltage σ m = (σ max + σ min ) /2 .

The processes of gradual accumulation of damage in a material under the influence of cyclic loads, leading to a change in its properties, the formation of cracks, their development and destruction, are called fatigue, and the properties to resist fatigue are called endurance (Fig. 7).

Failure from fatigue compared to failure from static load has a number of features:

1. It occurs at voltages lower than under static load;
2. Fracture begins locally at the surface;
3. Fracture occurs in several stages and has a characteristic fracture structure:
   crack initiation site;
4. fatigue zone. In this zone, characteristic grooves are visible, which have a ring configuration, which indicates the abrupt progression of a fatigue crack.
5. dolom zone.

The ability of a material to work under cyclic loading conditions is judged by the results of fatigue testing of samples. The test results are depicted in the form of a fatigue curve: σmax versus the number of loading cycles N. The horizontal section determines the stress that does not cause fatigue failure after an unlimited number of cycles. This stress represents the physical endurance limit σ R ( R is the cycle asymmetry coefficient), with a symmetric cycle σ -1 .

Fig.7 Endurance test

Fatigue curves allow you to determine the following endurance criteria:

• cyclic strength - the greatest stress that it can withstand for a certain operating time. Limited endurance limit;
• cyclic durability - the number of cycles (hours) that a material can withstand before the formation of a fatigue crack or before fatigue failure at a given stress.

Cyclic strength and durability depend on a large number of factors, of which the structure and stress state of the surface layer, surface quality and exposure to a corrosive environment are decisive. (Holes, grooves, grooves, grooves, pores, cavities, non-metallic inclusions, etc.).

Additional endurance criteria:

1. survivability – determined by the fatigue crack growth rate ( CFG ). With high survivability, it is possible to promptly detect a crack using flaw detection, replace the part and ensure trouble-free operation.
2. wear resistance – the property of a material to resist wear under certain friction conditions. Wear is the process of gradual destruction of the surface layers of a material by separating its particles under the influence of friction forces. It is determined by changes in size, volume or mass. There are three wear periods:
   initial, running-in period;
3. period of established (normal) wear;
4. period of catastrophic wear. A material that is resistant to wear in one environment can degrade catastrophically quickly in another.

This problem is solved by a rational choice of the material of the rubbing pairs and the method of processing it.

• creep - determined by the rate of development of plastic deformation of the material at constant stress and at high temperatures.

Thus, the performance of the part material under operating conditions is characterized by the following structural strength criteria:

1. strength criteria σв, σ0.2, σ-1, which, with a given safety factor, determine the permissible operating stresses, weight and dimensions of parts;
2. elastic modulus E, which, for a given part geometry, determines the magnitude of elastic deformations, i.e. its rigidity;
3. plasticity δ, ψ, impact strength KST, KSV, KSU, fracture toughness K, temperature threshold of cold brittleness T50, which evaluate the reliability of the material during operation;
4. cyclic durability, wear rates, creep, corrosion, which determine the durability of the material.

Wood tensile strength

Stretch along the fibers. The tensile strength of wood along the fibers depends relatively little on the moisture content of the wood, but drops sharply at the slightest deviation of the fibers from the direction of the longitudinal axis of the sample. On average, for all species, the tensile strength along the fibers is about 130 MPa. Despite such high strength, wood in structures and products rarely works in tension along the fibers due to the difficulty of preventing the destruction of parts at the points of fastening (under the influence of compressive and shearing forces). loads). Stretch across the fibers. From the data given in various sources, it follows that the tensile strength of wood across the fibers in the radial direction is greater than in the tangential direction, for coniferous species - by 10-50%, for deciduous species - by 20-70%. Hard disseminated-vascular hardwoods have the greatest strength, followed by ring-vascular hardwoods and then soft disseminated-vascular hardwoods. Coniferous species, compared to hardwood, have significantly lower tensile strength in both the radial and tangential directions. On average, the tensile strength along the grain is approximately 20 times greater than the tensile strength across the grain. Strength characteristics for the type of force under consideration are necessary for the development of cutting and drying conditions for wood. They limit the maximum values ​​of drying stresses, the achievement of which causes cracking of the material. When calculating safe wood drying conditions, the dependence of the strength limits on humidity and temperature, as well as the duration of the load, are taken into account. And when designing products, they are practically not used, because designers try to avoid loading. in which noticeable tensile loads act across the fibers.

Compressive strength of wood

Compression along the fibers. The compressive strength along the grain is the least variable compared to other properties of wood. In structures and products, wood very often works in compression along the fibers, which is explained by its high strength under this type of impact and the ease of their application. Typical types of failure during compression along the fibers can be identified. In species with easily deformable wood, as well as in all species with high wood humidity, collapse of the ends of the sample is observed. In rocks with increased rigidity, upon destruction, an oblique fold appears, usually located at an angle of 60-70″ on the tangential surface of the sample. Quite often you can find two opposing oblique folds in a destroyed sample, forming a wedge-shaped area, under which a crack from a longitudinal split is visible. Sometimes sample delamination and other types of destruction are observed. All this indicates a significant influence on the compressive strength along the fibers of the structural features and anisotropy of the mechanical properties of wood. Data on the strength limits of the most common rocks in Russia are given in Table 1.

Compression across the grain. There are three typical failure cases possible for this type of loading. The first is characteristic of coniferous wood (radial direction). First, the weak early wood of the annual layers is compressed, then, after the anatomical elements lose stability, the process of their collapse occurs, which does not require much additional effort. The last phase of deformation is not associated with destruction, since here the stronger and stiffer late wood begins to offer resistance and, despite heavy loads, only compaction of the wood occurs. The second type is characteristic of hardwoods in both radial and tangential directions. In this case, the second phase is less pronounced. A completely different picture is observed for coniferous wood under compression in the tangential direction. In this case, the forces are perceived simultaneously by the early and late zones of the annual layers. These are stronger zones and this circumstance leads to destruction of the sample. It bulges towards the convexity of the annual layers. Approximately the same nature of destruction is observed for dry oak wood in the radial direction. Research results show that the compressive strength across the grain for all rocks is approximately 10 times less than the compressive strength along the grain. No less interesting are the test data for local crushing across the fibers (determining the contact strength of wood). Here the impact does not occur on the entire surface of the part (sample), but only on a part of it. The local crushing strength due to the additional bending resistance of the fibers turns out to be slightly (20-25%) higher than with simple compression. Compression across the fibers occurs in the case of pressed wood, local compression occurs in the case of local impact on parquet, etc.

Mechanical properties of materials,

a set of indicators characterizing the resistance of a material to the load acting on it, its ability to deform in this case, as well as the features of its behavior during the process of destruction.
In accordance with this M. s. m are measured by stress (usually in kgf/mm2
or
Mn/m2
)
,
strain (in%), specific work of deformation and fracture (usually in
kgf
×
m/cm2
or
Mj/m2
)
,
the rate of development of the destruction process under static or repeated load (most often in
mm
per 1
sec
or per 1000 load repetition cycles,
mm/kcycle
)
.
M. s. m are determined during mechanical tests of samples of various shapes.

In general, materials in structures can be subjected to loads of very different nature ( Fig. 1

): work in
tension,
compression,
bending
,
torsion
, shear, etc. or are subject to the combined action of several types of load, such as tension and bending.
The operating conditions of materials are also varied in temperature, environment, speed of load application and the law of its change over time. In accordance with this, there are many indicators of M. s. m. and many mechanical testing methods. For metals and engineering plastics, the most common tests are tensile, hardness
, and impact bending; brittle structural materials (for example, ceramics, metal-ceramics) are often tested for compression and static bending; It is important to evaluate the mechanical properties of composite materials, in addition, during shear tests.

Deformation diagram.

A load applied to a sample causes its
deformation
.
The relationship between load and deformation is described by the so-called. strain diagram ( Fig. 2
).
Initially, the deformation of the sample (under tension - the increment in length Dl )
is proportional to the increasing load
P
, then at point
n
this proportionality is violated, however, to increase the deformation, a further increase in the load
P
;
when D l
> D
l
in, deformation develops without applying external force, with a gradually decreasing load. The appearance of the strain diagram does not change if stress is plotted along the ordinate axis

and along the x-axis - relative elongation

(F0

and
l0
are the initial cross-sectional area and the estimated length of the sample, respectively).

The resistance of materials is measured by stresses characterizing the load per unit cross-sectional area of ​​the sample

in kgf/mm2.

Voltage

at which the growth of deformation proportional to the load is violated, is called the limit of proportionality. At load P

<
Рn
unloading the sample leads to the disappearance of the deformation that arose in it under the influence of the applied force;
such deformation is called elastic. A slight excess of the load relative to Pn
may not change the nature of the deformation - it will still retain its elastic nature. The greatest load that a sample can withstand without the appearance of residual plastic deformation during unloading determines the elastic limit of the material:

In non-metallic structural materials (plastic, rubber), the applied load can cause elastic, highly elastic and residual deformation. Unlike elastic, highly elastic deformation does not disappear immediately after unloading, but over time. High-strength reinforced polymers (fiberglass, carbon fiber, etc.) are destroyed at an elongation of 1-3%. At the last stages of loading, some reinforced polymers exhibit highly elastic deformation. The highly elastic modulus is lower than the elastic modulus, so the deformation diagram in this case tends to deviate towards the x-axis.

Elastic properties.

In the elastic region, stress and strain are related by a proportionality coefficient.
When stretched, s = Ed, where E
is the so-called.
normal elastic modulus, numerically equal to the tangent of the angle of inclination of the straight section of the curve s = s(d) to the deformation axis ( Fig. 2
). When testing a cylindrical or flat sample for tension, a uniaxial (s1>0; (s2 = s3 = 0) stress state corresponds to a triaxial deformed state (an increase in length in the direction of the applied forces and a decrease in linear dimensions in two other mutually perpendicular directions): d1>0 ; d2 = d3 < 0. Relationship between transverse and longitudinal strain (Poisson's ratio)

within the elasticity range for basic structural materials it fluctuates within rather narrow limits (0.27–0.3 for steels, 0.3–0.33 for aluminum alloys). Poisson's ratio is one of the main calculation characteristics. Knowing m and E

, it is possible to determine the shear modulus by calculation

and bulk modulus

To determine E, G

, and m use
strain gauges
.

Resistance to plastic deformation.

At loads
P
>
Pb
, along with ever-increasing elastic deformation, noticeable irreversible plastic deformation appears, which does not disappear upon unloading. The stress at which the residual relative deformation (tensile elongation) reaches a given value (according to GOST - 0.2%) is called the conditional yield strength and is designated

In practice, the accuracy of modern testing methods is such that sp and se are determined with specified tolerances, respectively, for deviation from the law of proportionality [an increase in ctg(90 - a) by 25-50%] and for the amount of residual deformation (0.003-0.05%) and say about the conditional limits of proportionality and elasticity. The tensile curve of structural metals may have a maximum (point c in Fig. 2

) or break off when the maximum load
Рв
' is reached. Attitude

characterizes the temporary resistance (tensile strength) of the material. If there is a maximum on the tensile curve in the area of ​​loads lying on the curve to the left in

, the sample is deformed uniformly along the entire calculated length
l
0, gradually decreasing in diameter, but maintaining the initial cylindrical or prismatic shape.
During plastic deformation, metals are strengthened, therefore, despite the reduction in the cross-section of the sample, further deformation requires the application of an ever-increasing load. sв, like the conventional s0.2, sn and se, characterizes the resistance of metals to plastic deformation. In the section of the deformation diagram to the right, the shape of the tensile sample changes: a period of concentrated deformation begins, expressed in the appearance of a “neck”. The reduction in the cross-section in the neck “overtakes” the strengthening of the metals, which causes a drop in the external load in the section Pb - Pk
.

For many structural materials, the resistance to plastic deformation in the elastic-plastic region during tension and compression is almost the same. Some metals and alloys (for example, magnesium alloys, high-strength steels) are characterized by noticeable differences in this characteristic under tension and compression. Resistance to plastic deformation is especially often (when monitoring product quality, standard heat treatment conditions, and in other cases) assessed based on the results of hardness tests by pressing a hard tip in the shape of a ball (Brinell or Rockwell hardness), cone (Rockwell hardness) or pyramid (Vickers hardness). Hardness tests do not require violating the integrity of the part and therefore are the most widespread means of monitoring mechanical properties. Brinell hardness (HB) when indenting a ball with diameter D

under load
P
characterizes the average compressive stress, conventionally calculated per unit surface of a spherical imprint with diameter
d
:

Plasticity characteristics.

Tensile plasticity of structural materials is assessed by elongation

or narrowing

when compressed - shortening

(where h0

and
hk
- the initial and final height of the sample), in case of torsion - the maximum angle of twist of the working part of the sample Q,
rad
or relative shift g = Q
r
(where
r
is the radius of the sample).
The final ordinate of the deformation diagram (point k
in
Fig. 2
) characterizes the fracture resistance of the metal
Sk
, which is determined

(Fk

- actual area at the rupture site).

Characteristics of destruction.

Destruction does not occur instantly (at point
k
), but develops over time, and the beginning of destruction may correspond to some intermediate point in the section
vk
, and the whole process ends when the load gradually drops to zero.
The position of point k on the deformation diagram is largely determined by the rigidity of the testing machine and the inertia of the measuring system. This makes the value of Sk
largely arbitrary.

Many structural metals (steels, including high-strength, heat-resistant chromium-nickel alloys, soft aluminum alloys, etc.) fail in tension after significant plastic deformation with the formation of a neck. Often (for example, in high-strength aluminum alloys) the fracture surface is located at an angle of approximately 45° to the direction of the tensile force. Under certain conditions (for example, when testing cold-brittle steels in liquid nitrogen or hydrogen, when exposed to tensile stresses and a corrosive environment for metals prone to stress corrosion), fracture occurs along sections perpendicular to the tensile force (direct fracture), without macroplastic deformation.

The strength of materials realized in structural elements depends not only on the mechanical properties of the metal itself, but also on the shape and size of the part (the so-called shape and scale effects), the elastic energy accumulated in the loaded structure, the nature of the acting load (static, dynamic , periodically changing in magnitude), schemes for the application of external forces (uniaxial, biaxial stretching, with superimposed bending, etc.), operating temperature, environment. The dependence of the strength and ductility of metals on the shape is characterized by the so-called. sensitivity to notch, usually assessed by the ratio of the tensile strengths of notched and smooth samples

(for cylindrical samples, the cut is usually made in the form of a circular recess, for strips - in the form of a central hole or side cuts). For many structural materials, this ratio under static load is greater than unity, which is associated with significant local plastic deformation at the apex of the notch. The sharper the cut, the smaller the local plastic deformation and the greater the proportion of direct fracture in the failed section. A well-developed direct fracture can be obtained at room temperature in most structural materials in laboratory conditions, if samples with a massive cross-section (thicker, the more plastic the material is) are subjected to stretching or bending, providing these samples with a special narrow slot with an artificially created crack ( Fig. 3

).
When a wide, flat sample is stretched, plastic deformation is difficult and is limited to a small area of ​​size 2 ry
(shaded in
Fig. 3b
) immediately adjacent to the crack tip. Direct fracture is usually characteristic of operational failures of structural elements.

K1C , proposed by the American scientist J.R. Irwin as constants for conditions of brittle fracture, have become widespread.

and fracture toughness

In this case, the destruction process is considered in time and K1C

(
G1C
) refer to the critical moment when the stable development of the crack is disrupted; a crack becomes unstable and propagates spontaneously when the energy required to increase its length is less than the energy of elastic deformation arriving at the crack tip from adjacent elastically stressed zones of the metal.

When assigning sample thickness t

and crack sizes 2
ltr
are based on the following requirement

Stress intensity factor K

takes into account not only the load value, but also the length of the moving crack:

(l takes into account the geometry of the crack and the sample), expressed in kgf/mm3/2

or
Mn/m3/2.
By
K1C
or
G1C
one can judge the susceptibility of structural materials to brittle fracture under operating conditions.

To assess the quality of metal, bending impact tests on prismatic samples with a notch on one side are very common. In this case, impact strength

(in
kgf
×
m/cm2
or
MJ/m2
)
-
the work of deformation and destruction of the sample, conditionally related to the cross section at the notch location.
Impact bending tests on samples with an artificially created fatigue crack at the base of the notch have become widespread. atom
samples is generally in satisfactory agreement with such a fracture characteristic as
K1C
, and even better with the ratio

Time dependence of strength.

As the load duration increases, the resistance to plastic deformation and fracture resistance decrease.
At room temperature in metals, this becomes especially noticeable when exposed to a corrosive (stress corrosion) or other active (Rehbinder effect) environment. At high temperatures, the phenomenon of creep
, i.e., an increase in plastic deformation over time at constant stress (
Fig. 4
, a).
The creep resistance of metals is assessed by the conditional creep limit - most often the stress at which plastic deformation reaches 0.2% in 100 hours
, and is designated s0.2/100.
The higher the temperature t
, the more pronounced the phenomenon of creep and the more the resistance to destruction of the metal decreases over time (
Fig. 4
, b)
.
The last property is characterized by the so-called. limit of long-term strength, i.e. stress, which at a given temperature causes destruction of the material in a given time (for example, st100, st1000, etc.). In polymeric materials, the temperature-time dependence of strength and deformation is more pronounced than in metals. When plastics are heated, highly elastic, reversible deformation is observed; starting from a certain higher temperature, irreversible deformation develops associated with the transition of the material to a viscous-flow state. Another important mechanical property of materials is associated with creep—the tendency to stress relaxation, i.e., to a gradual drop in stress under conditions when the general (elastic and plastic) deformation maintains a constant specified value (for example, in tightened bolts). Stress relaxation is caused by an increase in the proportion of the plastic component of the total deformation and a decrease in its elastic part.

If the metal is subject to a load that periodically changes according to some law (for example, sinusoidal), then with an increase in the number of cycles N

load, its strength decreases (
Fig. 4
, c) - the metal “gets tired”.
For structural steel, such a drop in strength is observed up to N
= (2-5) × 106 cycles. In accordance with this, they talk about the fatigue limit of structural steel, usually meaning the stress amplitude

below which steel does not fail under repeated varying loads. At |smin| = |smax| The fatigue limit is designated by the symbol s-1. The fatigue curves of aluminum, titanium and magnesium alloys usually do not have a horizontal section, so the fatigue resistance of these alloys is characterized by the so-called. limited (corresponding to a given N

) limits of fatigue. Fatigue resistance also depends on the frequency of load application. The resistance of materials under conditions of low frequency and high levels of repeated loading (slow, or low-cycle, fatigue) is not clearly related to fatigue limits. In contrast to a static load, under repeated variable loads sensitivity to a notch always appears, i.e., the fatigue limit in the presence of a notch is lower than the fatigue limit of a smooth sample. For convenience, sensitivity to notch during fatigue is expressed by the ratio

characterizes the asymmetry of the cycle). In the fatigue process, one can distinguish a period preceding the formation of a source of fatigue failure, and following it, sometimes quite long, the period of development of a fatigue crack. The slower the crack develops, the more reliable the material in the structure works. Fatigue crack propagation rate dl/dN

is associated with the stress intensity factor by a power function:

A distinction is made between thermal fatigue resistance when the stresses that appear in the material are due to the fact that, for one reason or another, for example, due to the shape of the part or the conditions of its fastening, thermal movements occurring during cyclic temperature changes cannot be realized. Thermal fatigue resistance also depends on many other properties of the material - coefficients of linear expansion and thermal diffusivity, elastic modulus, elastic limit, etc.

Lit.:

Davidenkov N.N., Dynamic testing of metals, 2nd ed., L. - M., 1936; Ratner S.I., Failure under repeated loads, M., 1959; Serensen S.V., Kogaev V.P., Shneiderovich R.M., Load-bearing capacity and strength calculations of machine parts, 2nd ed., M., 1963; Applied issues of fracture toughness, trans. from English, M., 1968; Fridman Ya. B., Mechanical properties of metals, 3rd ed., M., 1974; Methods of testing, control and research of engineering materials, ed. A. T. Tumanova, vol. 2, M., 1974.

S. I. Kishkina.

Contents TSB