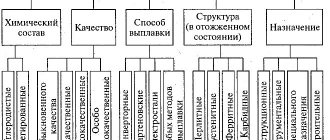
Strain diagram
shows the dependence of the change in the length of the sample with a gradual increase in the magnitude of the applied force (Fig. 21).
At the first moment of testing, the length of the sample increases in proportion to the load - the greater the tensile force, the greater the increase in length.
In this case, the sample is deformed elastically, i.e., when the load is removed, the sample will take on its original length. This deformation is called elastic deformation.
When the load P s
Noticeable
plastic deformation
—shifts of the metal layers relative to each other, and when the load is removed, the sample does not return to its original length.
The load corresponding to this moment P s ,
is called
the yield stress load.
Metal yield strength
The ratio of this load to the cross-sectional area is called the yield strength.
where F
- the initial cross-sectional area of the sample in mm 2.
As can be seen from the formula, the yield strength is measured in kg/mm
2 .
Values expressed in such units are called voltage.
Thus, the yield strength
is the stress at which noticeable plastic deformation begins to develop.
With a further increase in the load beyond the yield point, there is no longer a linear relationship between the load and the length of the sample. Finally, a moment comes when the load begins to drop, and a narrowing of the cross section is observed in the sample (neck formation).
Metal tensile strength
The maximum load that the sample withstood is called the ultimate strength load,
and the stress corresponding to this maximum load is
the tensile strength.
Thus, the tensile strength
is called the maximum voltage withstood by the sample.
Further stretching of the sample is accompanied by the formation of an increasingly narrowing neck and a drop in load. Following this comes destruction
sample.
Source: www.conatem.ru
Strength of materials (rupture of metals) under tension and compression: what is it, types, photos
When constructing objects, it is imperative to use calculations that include detailed characteristics of building materials. Otherwise, too much, unbearable load may be placed on the support, which will cause destruction. Today we’ll talk about the tensile strength of a material at break and tension, we’ll tell you what it is and how to work with this indication.
Specific strength formula
R with the index “y” is the designation of this parameter in physics. It is calculated as PP (in writing - R) divided by density - d. That is, this calculation has practical value and takes into account theoretical knowledge about the properties of steel for use in life. Engineers can tell how the temporary resistance changes depending on the mass and volume of the product. It is logical that the thinner the sheet, the easier it is to deform.
The formula looks like this:
Ry = R/d
Here it would be logical to explain how the specific tensile strength is measured. In N/mm2 - this follows from the proposed calculation algorithm.
Definition of the term
PP - we will use this abbreviation, and we can also talk about the official combination “temporary resistance” - this is the maximum mechanical force that can be applied to an object before its destruction begins. In this case, we are not talking about chemical effects, but we mean that heating, unfavorable climatic conditions, and a certain environment can either improve the properties of the metal (as well as wood, plastic) or worsen it.
No engineer uses extreme values when designing, because it is necessary to leave a permissible error - for environmental factors, for the duration of operation. We told you what is called tensile strength, now let’s move on to the specifics of the definition.
Definition of the term
Initially there were no special events. People took an item, used it, and as soon as it broke, they analyzed the breakdown and reduced the load on a similar product. Now the procedure is much more complicated, however, until now the most objective way to find out PP is the empirical way, that is, experiments and experiments.
All tests are carried out under special conditions with a large amount of precise equipment that records the condition and characteristics of the experimental material. Usually it is fixed and experiences various influences - tension, compression. They are performed by instruments with high precision - every thousandth of a newton of the applied force is noted. At the same time, each deformation is recorded as it occurs. Another method is not laboratory, but computational. But usually mathematical analysis is used in conjunction with testing.
Definition of the term
The sample is stretched on a testing machine. In this case, first it lengthens in size, and the cross-section becomes narrower, and then a neck is formed - the place where the thinnest diameter is, this is where the workpiece will rupture. This is true for ductile alloys, while brittle alloys, such as cast iron and hard steel, stretch very slightly without necking. Let's take a closer look at the video:
Tensile strength is determined by various influences, according to this it is classified according to:
- compression – mechanical pressure forces act on the sample;
- bending - the part is bent in different directions;
- torsion – suitability for use as a rotating shaft is checked;
- stretching - we gave a detailed example of testing above.
EQUIPMENT
1.1. Static devices or testing equipment are used as testing equipment, making it possible to:
smooth increase in load;
ensuring constant applied load for the required time;
suspension of loading with an accuracy of one smallest division of the force meter scale. The force meter scale division value should be no more than 1% of the load value at the yield point. The permissible relative load error should not exceed ± 1%;
application of the effective force perpendicular to the surface of the test product (sample).
1.2. Balls used for measuring hardness at the yield point must meet the following requirements:
material for balls - heat-treated steel with a hardness of at least 850 Vickers units;
the diameter of the balls used is 10, 20, 30, 40 and 50 mm;
maximum deviations in the diameter of the ball must comply with GOST 3722-60, in group B;
the roughness parameter Ra of the ball surface should be no more than 0.040 µm according to GOST 2789-73.
1.3. A ball that, after hardness measurement, has shown residual deformation exceeding the specified dimensional tolerance in accordance with group B of GOST 3722-60 or any surface defect must be replaced with another, and the corresponding measurement must be considered invalid.
1.4. To measure the diameter of an indentation, microscopes must be used that provide measurements with an error not exceeding:
± 0.0025 mm - when measuring hardness with a ball with a diameter of 10 mm;
± 0.005 mm » » » » » 20 mm;
± 0.0075 mm » » » » » 30 mm;
± 0.01 mm » » » » » 40 mm;
± 0.012 mm » » » » » 50 mm.
1.5. Periodic verification of instruments for determining hardness at the yield point is carried out in accordance with GOST 8.043-72.
Tensile strength of steel
Steel structures have long replaced other materials, as they have excellent performance characteristics - durability, reliability and safety. Depending on the technology used, it is divided into brands. From the most common with a PP of 300 MPa, to the hardest with a high carbon content - 900 MPa. This depends on two indicators:
- What heat treatment methods were used - annealing, hardening, cryotreatment.
- What impurities are contained in the composition. Some are considered harmful, they are discarded for the purity of the alloy, and others are added to strengthen them.
Strength classes and their designations
All categories are written down in regulatory documents - GOSTs, according to which all Russian entrepreneurs produce any rolled metal and other metal products. Here is the correspondence between the designation and parameter in the table:
| Class | Tensile strength, N/mm2 |
| 265 | 430 |
| 295 | 430 |
| 315 | 450 |
| 325 | 450 |
| 345 | 490 |
| 355 | 490 |
| 375 | 510 |
| 390 | 510 |
| 440 | 590 |
We see that for some classes the PP indicators remain the same, this is explained by the fact that, with equal values, their fluidity or relative elongation may differ. Depending on this, different maximum thickness of rolled metal is possible.
Proportionality limit
This is an indicator that determines the duration of the loads applied to the deformation of the body. In this case, both values should change to different degrees according to Hooke’s law. In simple words: the greater the compression (tension), the more the sample is deformed.
The value of each material lies between absolute and classical elasticity. That is, if the changes are reversible after the force ceases to act (the shape becomes the same - for example, compression of a spring), then such parameters cannot be called proportional.
How are the properties of metals determined?
They check not only what is called tensile strength, but also other characteristics of steel, for example, hardness. The tests are carried out as follows: a ball or cone made of diamond, the most durable rock, is pressed into the sample. The stronger the material, the smaller the mark left. Deeper, wider-diameter prints are left on soft alloys. Another experience - for a blow. The impact occurs only after a pre-made cut on the workpiece. That is, the destruction is checked for the most vulnerable area.
PREPARATION FOR CONTROL
2.1. The roughness parameter Ra of the surface of the product (sample) at the test site should be no more than 0.32 µm according to GOST 2789-73.
2.2. When preparing the surface of the test product (sample), it is necessary to take precautions to prevent changes in the hardness of the test product (sample) due to heating or hardening of the surface during machining.
2.3. The test product (sample) should not move when measuring hardness.
2.4. The minimum thickness of the product (sample) must be at least 8 times the depth of the print.
2.5. The distance from the center of the print to the edge of the sample must be at least 1.5 times the diameter of the print, and the distance between the centers of two adjacent prints must be at least twice the diameter of the print.
2.6. When measuring hardness on products (samples) with a convex cylindrical surface, the minimum radius of curvature of the product (sample) must be at least five diameters of the ball. In this case, the test must be carried out without preparing a flat surface.
When measuring hardness on products (samples) with a cylindrical surface, in which the radius of curvature is less than five diameters of the ball, the width and length of the prepared flat surface must be at least five diameters of the print, respectively. The distance from the center of the print to the boundary between the flat and cylindrical surfaces must be at least 1.5 times the diameter of the print.
Mechanical properties
There are 5 characteristics:
- The tensile and tensile strength of steel is temporary resistance to external forces, stress arising internally.
- Plasticity is the ability to deform, change shape, but maintain the internal structure.
- Hardness – willingness to meet harder material without causing significant damage.
- Impact strength is the ability to resist impacts.
- Fatigue is the duration of preservation of qualities under the influence of cyclic loads.
Tensile strength
A certain threshold value for a specific material, exceeding which will lead to the destruction of the object under the influence of mechanical stress. The main types of strength limits: static, dynamic, compressive and tensile. For example, the tensile strength is the limit value of a constant (static limit) or variable (dynamic limit) mechanical stress, exceeding which will rupture (or unacceptably deform) the product. Unit of measurement: Pascal [Pa], N/mm² = [MPa].
Yield strength (σt)
The amount of mechanical stress at which the deformation continues to increase without increasing the load; used for calculating permissible stresses in plastic materials.
After passing the yield point, irreversible changes are observed in the metal structure: the crystal lattice is rearranged, and significant plastic deformations appear. At the same time, self-strengthening of the metal occurs and after the yield point, the deformation increases with increasing tensile force.
This parameter is often defined as “the stress at which plastic deformation begins to develop” [1], thus identifying the limits of yield and elasticity. However, it should be understood that these are two different parameters. The yield strength values exceed the elastic limit by approximately 5%.
PROCESSING RESULTS
4.1. Hardness at yield point ( N
0.2) in MPa (kgf/mm2) is determined from the table. 1 and 2 given in the mandatory annex, or calculated using the formula
where P
— load in N corresponding to the diameter of the indentation
d
= 0.09
D
;
D
— ball diameter, mm;
d
— imprint diameter, mm.
4.2. When indicating hardness at the yield point, the calculated value is supplemented with the symbol H
0.2 indicating the dimension, for example: 250
H
0.2, MPa.
4.3. When pressing a ball with a diameter of 20, 30, 40, 50 mm load P
0.2 must be divided by 4 accordingly;
9; 16; 25 and, based on the result obtained from division, determine the desired hardness value H
0.2.
For example: when pressing a ball with diameter D
= 40 mm to the indent diameter
d =
3.6 mm, the load at the yield point turned out to be equal to 3200 N. Then, to determine the hardness value, it is necessary to divide the load of 3200 N by and according to the table.
1 for a load value of 200 N, find the corresponding value of hardness at the yield strength H
0.2, equal to 314 MPa.
4.4. According to hardness values at the yield point H
0.2, the tensile yield strength
s
0.2 can be determined at the test location.
The relationship between the load at the yield point P
0.2
,
the hardness at the yield point
H
0.2 and the yield strength
s
0.2 for alloy steels when tested with a ball with a diameter of 10 mm is given in the table.
Determination error s
0.2 according to
H
0.2 is ± 7%.
| P 0.2, N (kgf) | H 0.2, MPa (kgf/mm2) | s0.2, MPa (kgf/mm2) | P 0.2, N (kgf) | H 0.2, MPa (kgf/mm2) | s0.2, MPa (kgf/mm2) |
| 451 (46) | 708 (72,2) | 201 (20,5) | 981 (100) | 1539 (156,9) | 490 (50,0) |
| 471 (48) | 738 (76,3) | 211 (21,5) | 1000 (102) | 1569 (160,0) | 505 (51,5) |
| 490 (50) | 769 (78,4) | 221 (22,5) | 1020 (104) | 1600 (163,2) | 520 (53,0) |
| 510 (52) | 800 (81,6) | 231 (23,5) | 1040(106) | 1631 (166,3) | 535 (54,5) |
| 530 (54) | 831 (84,7) | 237 (24,2) | 1059 (108) | 1661 (169,4) | 549 (56,0) |
| 549 (56) | 862 (87,9) | 245 (25,0) | 1079 (110) | 1693 (172,6) | 559 (57,0) |
| 569 (58) | 892 (91,0) | 250 (25,5) | 1098 (112) | 1723 (175,7) | 579 (59,0) |
| 588 (60) | 923 (94,1) | 260 (26,5) | 1118 (114) | 1753 (178,8) | 593 (60,5) |
| 608 (62) | 954 (97,3) | 270 (27,5) | 1138 (116) | 1785 (182,0) | 608 (62,0) |
| 628 (64) | 985 (100,4) | 280 (28,5) | 1157 (118) | 1815 (185,1) | 623 (63,5) |
| 647 (66) | 1015 (103,5) | 289 (29,5) | 1177 (120) | 1847 (188,3) | 637 (65,0) |
| 667(68) | 1046 (106,7) | 299 (30,5) | 1196 (122) | 1877 (191,4) | 652 (66,5) |
| 687 (70) | 1077 (109,8) | 309 (31,5) | 1216 (124) | 1907 (194,5) | 667 (68,0) |
| 706 (72) | 1108 (113,0) | 319 (32,5) | 1236 (126) | 1939 (197,7) | 682 (69,5) |
| 726 (74) | 1139 (116,1) | 329 (33,5) | 1255 (128) | 1969 (200,8) | 696 (71,0) |
| 745 (76) | 1169 (119,2) | 338 (34,5) | 1275 (130) | 2000 (203,9) | 711 (72,5) |
| 765 (78) | 1200 (122,4) | 353 (36,0) | 1295 (132) | 2031 (207,1) | 726 (74,0) |
| 785 (80) | 1231 (125,5) | 363 (37,0) | 1314 (134) | 2061 (210,2) | 745 (76,0) |
| 804 (82) | 1261 (128,6) | 373 (38,0) | 1334 (136) | 2093 (213,4) | 760 (77,5) |
| 824 (84) | 1293 (131,8) | 387 (39,5) | 1353 (138) | 2123 (216,5) | 775 (79,0) |
| 843 (86) | 1323 (134,9) | 397 (40,5) | 1373 (140) | 2154 (219,6) | 794 (81,0) |
| 863 (88) | 1354 (138,1) | 412 (42,0) | 1393 (142) | 2185 (222,6) | 809 (82,5) |
| 883 (90) | 1385 (141,2) | 422 (43,0) | 1412 (144) | 2215 (225,9) | 824 (84,0) |
| 902 (92) | 1415 (144,3) | 436 (44,5) | 1432 (146) | 2246 (229,0) | 843 (86,0) |
| 922 (94) | 1447 (147,5) | 451 (46,0) | 1451 (148) | 2277 (232,2) | 963 (88,0) |
| 941 (96) | 1477 (150,6) | 461 (47,0) | 1471 (150) | 2308 (235,3) | 883 (90,0) |
| 961 (98) | 1507 (153,7) | 476 (48,5) | 1491 (152) | 2339 (238,5) | 902 (92,0) |
| 1510 (154) | 2369 (241,6) | 922 (94,0) | 1804 (184) | 2831 (288,7) | 1214 (123,8) |
| 1530 (156) | 2400 (244,7) | 941 (96,0) | 1824 (186) | 2862 (291,8) | 1232 (125,6) |
| 1550 (158) | 2431 (247,9) | 961 (98,0) | 1844 (188) | 2892 (294,9) | 1249 (127,4) |
| 1569 (160) | 2462 (251,0) | 981 (100,0) | 1863 (190) | 2993 (298,1) | 1267 (129,2) |
| 1589 (162) | 2492 (254,1) | 1000 (102,0) | 1883 (192) | 2954 (301,2) | 1286 (131,1) |
| 1608 (164) | 2523 (257,3) | 1020 (104,0) | 1902 (194) | 2984 (304,3) | 1302 (132,8) |
| 1628 (166) | 2554 (260,4) | 1040 (106,0) | 1922 (196) | 3016 (307,5) | 1322 (134,8) |
| 1648 (168) | 2585 (263,6) | 1059 (108,0) | 1942 (198) | 3046 (310,6) | 1341 (136,7) |
| 1667 (170) | 2615 (266,7) | 1079 (110,0) | 1961 (200) | 3077 (313,8) | 1359 (138,6) |
| 1687 (172) | 2646 (269,8) | 1198 (112,0) | 1981 (202) | 3108 (316,9) | 1378 (140,5) |
| 1706 (174) | 2677 (273,0) | 1118 (114,0) | 2001 (204) | 3138 (320,0) | 1396 (142,3) |
| 1726 (176) | 2708 (276,1) | 1138 (116,0) | 2020 (206) | 3170 (323,2) | 1414 (144,2) |
| 1746 (178) | 2738 (279,2) | 1157 (118,0) | 2040 (208) | 3200 (326,3) | 1434 (146,2) |
| 1765 (180) | 2770 (282,5) | 1177 (120,0) | 2059 (210) | 3230 (329,4) | 1451 (148,0) |
| 1785 (182) | 2780 (285,5) | 1196 (122,0) | 2079 (212) | 3262 (332,6) | 1471 (150,0) |
Endurance limit or fatigue limit (σR)
The ability of a material to withstand loads that cause cyclic stress. This strength parameter is defined as the maximum stress in a cycle at which fatigue failure of the product does not occur after an indefinitely large number of cyclic loads (the basic number of cycles for steel is Nb = 10 7 ). The coefficient R (σR) is taken to be equal to the cycle asymmetry coefficient. Therefore, the fatigue limit of the material in the case of symmetric loading cycles is denoted as σ-1, and in the case of pulsating ones - as σ.
Note that fatigue tests of products are very long and labor-intensive; they involve the analysis of large volumes of experimental data with an arbitrary number of cycles and a significant scatter of values. Therefore, special empirical formulas are most often used that connect the endurance limit with other strength parameters of the material. The most convenient parameter is considered to be the tensile strength.
For steels, the bending endurance limit is usually half the tensile strength: For high-strength steels, you can take:
For ordinary steels during torsion under conditions of cyclically changing stresses, the following can be accepted:
The above ratios should be used with caution, because they were obtained under specific loading conditions, i.e. during bending and torsion. However, when testing in tension-compression, the endurance limit becomes approximately 10-20% less than in bending.
Relationship between yield stress and tensile strength
and tensile strength is established by the relationship between the extrapolated yield strength and σ B. Since the extrapolated yield stress can be used to fairly accurately determine the yield stress for most materials, starting with the degree of deformation , this assumption can be considered justified.
Below we consider the relationships between the tensile strength and the extrapolated yield strength of the hardening curves under tension of the first kind and under compression of the second kind.
The extrapolated yield strength of the first-order tensile hardening curves is found at the intersection of the tangent to the hardening curve at the point where necking begins with the ordinate. For hardening curves of the second kind under compression, the extrapolated yield strength S0 (see Fig. 1) is the stress corresponding in magnitude to the ordinate segment cut off by the straight line, which is a continuation of section III of the hardening curve.
According to the theoretical calculations of M.P. Markovets for materials with uniform relative transverse contraction Ψ B
no more than 0.15, the difference between the extrapolated yield strength determined from the tensile hardening curves and the tensile strength σ
B
does not exceed 3%, and with Ψ
B
up to 0.2 - no more than 7%.
In this case, it should always be less than the value of
σ B.
The theoretically established relationship between and σ B
M.P.
Markovets confirmed it experimentally. It was shown that, regardless of the type of material (non-ferrous and ferrous metals), the type of previous heat treatment (annealing, normalization, hardening, hardening + tempering) and strength (the materials studied were 20-180 kg/mm2), the ratio for materials with up to 15% close to unity (Fig. 1). Only for brass and austenitic steel EI69, for which the value of Ψ B
reaches 30%, this ratio is 1.2-1.3.
P. Markovets also did a lot of work on comparing and σ B
according to experimental data from other researchers - N.N. Davidenkov, Kerber and Roland.
It was found that the data of various authors, obtained experimentally in different laboratories on a huge number of metals and alloys (aluminum, copper and their alloys, carbon and alloy steels) at room and elevated temperatures (from 20 to 300°C), confirm the theoretically established pattern for metals and alloys for which Ψ B
does not exceed 15%.
Let us experimentally determine the relationship between the extrapolated compressive yield stress S0 and σ B
.
Carbon and alloy hot-rolled and heat-treated steels served as the material under study (Table 1). Strengthening curves were plotted based on the results of upsetting of samples with cylindrical end recesses. The comparison results are graphically depicted in Fig. 1, from which it can be seen that there is a linear relationship between the values of S0 and σ B
, regardless of the brand of the product and the type and mode of pre-treatment.
Mathematical processing of experimental data shows that S0 is on average less than σ B
by about 6%, i.e.
The experimental data obtained are consistent with the experimental and theoretical data of M. P. Markovets on the relationship between the extrapolated tensile yield strength and σ B
in the sense that S0 is less than σ
B
by approximately the same amount.
Table 1
Chemical composition and type of previous processing of steels for which a relationship was established between the extrapolated compressive yield strength S0 and the ultimate strength σ B
| Steel | Previous processing | Element content in % | |||||
| C | Mn | Si | Cr | Ni | Mo | ||
| 10 | Hot rolling | 0,11 | 0,45 | 0,21 | — | — | — |
| 15 | Same | 0,15 | 0,43 | 0,27 | — | — | — |
| 20 | » | 0,19 | 0,37 | 0,37 | — | — | — |
| 15X | » | 0,13 | 0,42 | 0,32 | 0,90 | — | — |
| 20X | » | 0,24 | 0,67 | 0,25 | 0,91 | — | — |
| 45X | » | 0,44 | 0,61 | 0,19 | 0,90 | — | — |
| 12ХНЗА | » | 0,13 | 0,26 | 0,64 | 2,95 | — | |
| 12ХНЗА | Annealing, normalization | 0,16 | 0,40 | 0,36 | 0,66 | 2,81 | — |
| 40ХНМА | Annealing, normalization, improvement (t0 mn=600°C) | 0,37 | 0,60 | 0,24 | 0,66 | 1,39 | 0,15-0,25 |
Proportional limit (σ)
The maximum stress value for a particular material at which Hooke’s law still applies, i.e. The deformation of the body is directly proportional to the applied load (force). Please note that for many materials, reaching (but not exceeding!) the elastic limit leads to reversible (elastic) deformations, which, however, are no longer directly proportional to stress. In this case, such deformations may be somewhat “lag” relative to the increase or decrease in load.
Diagram of the deformation of a metal sample under tension in the coordinates elongation (Є) - stress (σ).
Source: www.smalley.ru
BASIC POINTS
Metals and alloys used as structural materials must have certain mechanical properties - strength, elasticity, ductility, hardness.
Strength is the ability of a metal to resist deformation and destruction.
Deformation is a change in the size and shape of a body under the influence of external forces. Deformations are divided into elastic and plastic. Elastic deformations disappear, and plastic deformations remain after the end of the forces. Plastic deformations are based on irreversible movements of atoms from their original positions to distances greater than interatomic distances, changes in the shape of individual metal grains, and their location in space.
The ability of metals to deform plastically is called plasticity. Plasticity ensures the structural strength of parts under load and neutralizes the influence of stress concentrates - holes, cutouts, etc. During plastic deformation of a metal, simultaneously with a change in shape, a number of properties change; in particular, during cold deformation, strength increases, but ductility decreases.
Most of the mechanical characteristics of the metal are determined by tensile testing of samples (GOST 1497-84).
When stretching samples with cross-sectional area Fo and working (calculated) length lo, a tensile diagram is constructed in the coordinates: load P – elongation Dl of the sample (Fig. 1).
The tensile diagram characterizes the behavior of the metal during deformation from the moment the loading begins until the destruction of the sample. The diagram distinguishes three sections: elastic deformation - up to load Rupr; uniform plastic deformation from Rupr to Pmax and concentrated plastic deformation from Pmax to Pk. If the sample is loaded within the limits of Rupr, and then completely unloaded and its length is measured, then no consequences of loading will be detected. This type of sample deformation is called elastic. When the sample is loaded more than Rupr, residual (plastic) deformation appears. Plastic deformation occurs under increasing load, since the metal is strengthened during deformation. Hardening of metal during deformation is called cold hardening. With further loading, the plastic deformation, and with it the hardening, increases more and more, evenly distributed throughout the entire volume of the sample. After reaching the maximum value of the load Pmax, a local thinning of the sample appears in the weakest place - the neck, in which further plastic deformation mainly occurs. At this time, cracks may appear between the deformed grains, and sometimes even inside the grains themselves. Due to the development of the neck, despite the continuing strengthening of the metal, the load decreases from Pmax to Pk, and at load Pk the sample is destroyed. In this case, the elastic deformation of the sample (Dlур) disappears, but the plastic deformation (Dlоst) remains (Fig. 1).
Rice. 1. Metal tensile diagram
When a solid body is deformed, internal forces arise inside it. The magnitude of forces per unit cross-sectional area of the sample is called stress. Voltage dimension kgf/mm
2 or
MPa
(1
kgf/mm2
=10
MPa
). The above-mentioned loads on the tensile curve (Rupr, Рт, Рmax, Рк) serve to determine the main characteristics of strength (stresses): elastic limit, physical yield strength, tensile strength (tensile strength) and true fracture resistance.
In technical calculations, instead of the ultimate strength, the conditional yield strength is usually used, which corresponds to the load P0.2 (Fig. 2).
Rice. 2. Section of the metal tensile diagram
When stretched, the sample elongates and its cross-section continuously decreases. But since it is difficult to determine the cross-sectional area of a sample at any given moment, when calculating the elastic limit, yield strength and tensile strength, conditional stresses are used, assuming that the cross-section of the sample remains unchanged. The true stress is calculated only when determining the fracture resistance. Conditional yield strength (s0.2) is the stress at which the sample receives a residual (plastic) elongation equal to 0.2% of its calculated length:
,
where P0.2 is the load causing residual (plastic) elongation equal to 0.2%, kgf
(N);
Fо – initial cross-sectional area of the sample,
mm2
.
Tensile strength (tensile strength) sв is the stress corresponding to the greatest load preceding the failure of the sample.
,
where Pmax is the maximum load preceding failure, kgf (H)
. Temporary resistance (tensile strength) characterizes the load-bearing capacity of a material, its strength prior to destruction. True fracture strength (Sk) – true stress preceding the moment of sample failure
,
where Pk is the load immediately preceding the moment of destruction, kgf (N)
.
Fк – cross-sectional area of the sample at the point of destruction, mm2
.
Despite the fact that Pmax is greater than Pk, the true fracture resistance Sc > sв, since the cross-sectional area of the sample at the point of destruction Fк is significantly less than the initial cross-sectional area Fo.
To assess the ductility of a metal, use the relative elongation of the sample under tension (d, %
) and the relative narrowing of the cross-sectional area of the sample (y,
%
).
Relative elongation after rupture (d, %
) is determined by the formula:
where lк is the working length of the sample after testing, mm
;
lо – working length before testing, mm
.
Relative narrowing of the cross section after rupture (y, %
) is determined from the expression:
where Fo is the initial cross-sectional area of the sample, mm2
;
Fк – cross-sectional area of the sample together with destruction, mm2
.
In practice, to determine the load that causes deformation corresponding to the proof stress, the following steps should be performed. On the tension diagram, draw a straight line OA (Fig. 2), coinciding with the straight section of the tension diagram. Determine the position of point O. Draw the ordinate axis OP through point O. The scale of recording the diagram by load: one millimeter of ordinate corresponds to 2 kgf
loads.
The numerical value of the required load P ( kgf
) is equal to the corresponding ordinate of the diagram (
mm
) multiplied by the scale of the diagram (2
kgf/mm
).
To determine the load corresponding to the conditional yield strength P0.2, it is necessary to plot a segment OB from the origin along the abscissa axis, the value of which is equal to the specified residual elongation of 0.2%. The length of the segment OB ( mm
) is calculated by the formula:
,
where lо – working length of the sample, mm
; M – scale of deformation diagram recording.
From point B, draw a straight line VD parallel to the straight section of the tension diagram (Fig. 2) until it intersects with the diagram.
Using the known scale of recording the load diagram, determine the numerical values of the loads P02, Pmax, Pk, and then calculate the corresponding voltage: s0.2, sv, Sk. Record the obtained data in the test report.