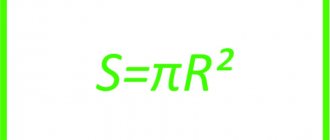Hexagon area calculator
A hexagon or hexagon is a regular polygon in which the sides are equal to each other and each angle is exactly 120 degrees.
A hexagon is sometimes found in human everyday life, so you may need to calculate its area not only in school problems, but also in real life. A heskagon is a regular convex polygon, accordingly, all its angles are equal, all sides are equal, and if you draw a segment through two adjacent vertices, then the entire figure will be on one side of this segment. As with any regular n-gon, you can draw a circle around the hexagon or inscribe it inside. The main feature of a hexagon is that the length of the radius of the circumscribed circle coincides with the length of the side of the polygon. Thanks to this property, you can easily find the area of a hexagon using the formula:
S = 2.59 R2 = 2.59 a2.
In addition, the radius of the inscribed circle is related to the side of the figure as:
r = 3.46 a.
It follows from this that the area of a hexagon can be calculated using one of three variables to choose from.
Hexagram
A star-shaped regular hexagon appears before us in the form of a six-pointed star. Such a figure is formed by superimposing two equilateral triangles on top of each other. The most famous real hexagram is the Star of David - a symbol of the Jewish people.
Calculation
The required value can be calculated by dividing the figure into six triangles with equal sides.
To calculate S , use the following formula:
Having calculated the S of one of the triangles, it is not difficult to determine the general one. A simple formula, since a regular hexagon is essentially six equal triangles. Thus, to calculate it, the found area of one triangle is multiplied by 6.
If you draw a perpendicular from the center of the hexagon to any of its sides, you get a segment - apothem .
Let's see how to find S of a hexagon if the apothem is known:
- S =1/2×perimeter×apothem.
- Let's take an apothem equal to 5√3 cm.
- Find the perimeter using the apothem: since the apothem is perpendicular to the side of the hexagon, the angles of the triangle formed using the apothem are 30˚-60˚-90˚. Each side of the triangle corresponds to: xx√3-2x, where the short one, against the 30˚ angle, is x; the long side against the angle 60˚ is x√3, and the hypotenuse is 2x.
- The apothem x√3 can be substituted into the formula a=x√3. If the apothem is equal to 5√3, substituting this value, we get: 5√3cm=x√3, or x=5cm.
- The short side of the triangle is 5 cm, since this value is half the length of the side of the hexagon. Multiplying 5 by 2, we get 10cm, which is the length of the side.
- Let's multiply the resulting value by 6 and get the perimeter value - 60 cm.
We substitute the obtained results into the formula: S=1/2×perimeter×apothem
S=½×60 cm×5√3
We count:
We simplify the answer received to get rid of the roots. The result will be expressed in square centimeters: ½×60cm×5√3cm=30×5√3cm=150√3cm=259.8s m².
Hexagonal numbers
In number theory, there are figured numbers associated with certain geometric figures. The most widely used numbers are triangular and square, as well as tetrahedral and pyramidal numbers, using which it is easy to lay out geometric shapes using real objects. For example, pyramid numbers will tell you how to stack cannonballs into a stable pyramid. There are also hexagonal numbers that determine the number of points required to construct a hexagon.
Selecting consumables for welding
To cook aluminum with an inverter without argon, electrodes made of a material similar in composition are used.
When heated, their coating creates a gaseous environment that prevents the penetration of air into the welding zone. The best domestic brands were recognized as OZA, OZR, OZANA. Foreign-made analogues OK 96.20, OK 96.40, Kobatek-213 are better in quality, but are more expensive. Argon arc welding is performed with non-consumable tungsten electrodes. To create a seam, filler wire with a diameter of 2 to 5 mm is used. Popular brands AO, AD, AK contain a lot of magnesium.
To weld aluminum with a semi-automatic inverter, filler wire with a diameter of 0.8 to 1 mm is used in 0.5 kg coils. The most popular brands are ER 4043 and ER 5356, made from an alloy of silicon and aluminum. Sv-AK 5 and Sv-AMg made of aluminum with magnesium are used less frequently.
Hexagon in reality
Hexagons are often found in real life. For example, the sections of nuts or pencils have a hexagonal shape, which ensures a comfortable grip on the object. A hexagon is an effective geometric shape that can tile a plane without gaps or overlaps. That is why decorative finishing materials, such as tiles and paving slabs or plasterboard panels, often have a hexagonal shape.
The effectiveness of the hexagon makes it popular in nature. Bee honeycombs have a hexagonal shape, thanks to which the space of the hive is filled without gaps. Another example of hexagonal tiling of a plane is the Giant's Causeway, a wildlife monument formed during a volcanic eruption. Volcanic ash was compressed into hexagonal columns that paved the surface of the Northern Ireland coastline.
From theory to practice
The properties of the hexagon are very actively used both in nature and in various fields of human activity. First of all, this applies to bolts and nuts - the heads of the first and second are nothing more than a regular hexagon, if you do not take the chamfers into account. The size of the wrenches corresponds to the diameter of the inscribed circle - that is, the distance between opposite edges.
Hexagonal tiles have also found their use. It is much less common than the quadrangular one, but it is more convenient to lay it: three tiles meet at one point, rather than four. The compositions can turn out to be very interesting:
Concrete tiles for paving are also produced.
The prevalence of hexagons in nature is simply explained. Thus, it is easiest to fit circles and balls tightly on a plane if they have the same diameter. Because of this, honeycombs have this shape.
The presentation was published 5 years ago by Grigory Oskin
Similar presentations
Packing circles on a plane
And a little more about the effectiveness of the hexagon. Packing balls is a classic problem in combinatorial geometry that requires finding the optimal way to pack disjoint balls. In practice, this task turns into a logistical problem of packing oranges, apples, cannonballs or any other spherical objects that need to be packed as tightly as possible. Heskagon is the solution to this problem.
It is known that the most efficient arrangement of circles in two-dimensional space is to place the centers of the circles on the vertices of hexagons that fill the plane without gaps. In three-dimensional reality, the problem of placing balls is solved by hexagonally arranging objects.
Using our calculator, you can calculate the area of a regular hexagon, knowing its side or the radii of the corresponding circles. Let's try to calculate the areas of hexagons using real examples.
What to do with a regular polygon that has more than four vertices?
To begin with, such a figure is characterized by the fact that all sides are equal. Plus, the polygon has equal angles.
If you draw a circle around such a figure, then its radius will coincide with the segment from the center of the polygon to one of the vertices. Therefore, in order to calculate the area of a regular polygon with an arbitrary number of vertices, you will need the following formula:
Sn = 1/2 * n * Rn2 * sin (360º/n), where n is the number of vertices of the polygon.
From it it is easy to obtain one that is useful for special cases:
- triangle: S = (3√3)/4 * R2;
- square: S = 2 * R2;
- hexagon: S = (3√3)/2 * R2.
Real life examples
Giant hexagon
The giant hexagon is a unique atmospheric phenomenon on Satur that looks like a huge vortex in the shape of a regular hexagon. It is known that the side of the giant hexagon is 13,800 km, thanks to which we can determine the area of the “cloud”. To do this, just enter the side value into the calculator form and get the result:
S = 494,777,633
Thus, the area of the atmospheric vortex on Saturn is approximately 494,777,633 square kilometers. Truly impressive.
Hexagonal chess
We are all accustomed to a chessboard divided into 64 square cells. However, there is also hexagonal chess, the playing field of which is divided into 91 regular hexagons. Let's determine the area of the game board for the hexagonal version of the famous game. Let the side of the cell be 2 centimeters. The area of one game cell will be:
S = 10.39
Then the area of the entire board will be 91 × 10.39 = 945.49 square centimeters.
Tasks
No. 1. Condition. There is a regular hexagonal prism, each edge of which is 4 cm. A cylinder is inscribed in it, the volume of which must be found.
Solution. The volume of a cylinder is defined as the product of the area of the base and the height. The latter coincides with the edge of the prism. And it is equal to the side of a regular hexagon. That is, the height of the cylinder is also 4 cm.
To find out the area of its base, you will need to calculate the radius of the circle inscribed in the hexagon. The formula for this is given above. This means r = 2√3 (cm). Then the area of the circle: S = π * r2 = 3.14 * (2√3)2 = 37.68 (cm2).
It remains to calculate the volume: V = 37.68 * 4 = 150.72 (cm3).
Answer. V = 150.72 cm3.
No. 2. Condition. Calculate the radius of a circle inscribed in a regular hexagon. It is known that its side is √3 cm. What will its perimeter be equal to?
Solution. This problem requires the use of two of the following formulas. Moreover, they must be applied without even modifying them, just substitute the value of the side and calculate.
Thus, the radius of the inscribed circle is equal to 1.5 cm. For the perimeter, the following value turns out to be correct: 6√3 cm.
Answer. r = 1.5 cm, P = 6√3 cm.
No. 3. Condition. The radius of the circumscribed circle is 6 cm. What value will the side of a regular hexagon have in this case?
Solution. From the formula for the radius of a circle inscribed in a hexagon, one easily obtains the one by which you need to calculate the side. It is clear that the radius is multiplied by two and divided by the root of three. It is necessary to get rid of irrationality in the denominator. Therefore, the result of the actions takes the following form: (12 √3) / (√3 * √3), that is, 4√3.
Answer. a = 4√3 cm.
Elements
For any prism, its main elements are edges, faces and vertices. The hexagonal prism is no exception. The above figure allows you to count the number of these elements. So, we get 8 faces or sides (two bases and six lateral parallelograms), the number of vertices is 12 (6 vertices for each base), the number of edges of a hexagonal prism is 18 (six lateral and 12 for the bases).
In the 1750s, Leonhard Euler (Swiss mathematician) established for all polyhedra, to which the prism belongs, a mathematical relationship between the numbers of the indicated elements. This relationship looks like:
number of edges = number of faces + number of vertices - 2.
The above figures satisfy this formula.
Interesting Facts
The shape of a regular hexagon is found in honeycombs, the cross-section of nuts and pencils, and the crystal lattice of graphite.
With the question: “How to find the area of a hexagon?” , you can encounter not only in a geometry exam, etc., this knowledge is also useful in everyday life, for example, for correctly and accurately calculating the area of a room during the renovation process. By substituting the required values into the formula, you will be able to determine the required number of rolls of wallpaper, tiles for the bathroom or kitchen, etc.