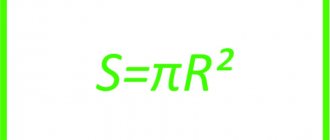How to Draw a Hexagon Using a Ruler

Cordless drill HAMMER ACD14BS

4699 ₽ More details

XXI CENTURY Candy Fudge Fragrant water 266 ₽ More details

HAMMER

The construction of a hexagon can be done in several ways. It is most convenient to use a standard set of drawing tools: a compass, a ruler. However, in the absence of a compass, a figure of this type can be drawn using a gauge, a factory-made square with angles of 90/60/30°.

Hexagons are used for loosening and tightening bolts when repairing and assembling furniture.

In both cases, a feature of the construction is an elementary knowledge of the basics of geometry. In a regular hexagon, the length of its side is always equal to the radius of the circle described around it, the opposite sides are parallel, the edges meet at an angle of 60°.

Definition and construction

A regular hexagon is a plane figure that has six sides of equal length and the same number of equal angles.

If we recall the formula for the sum of the angles of a polygon

it turns out that in this figure it is equal to 720°. Well, since all the angles of the figure are equal, it is not difficult to calculate that each of them is equal to 120°.

Drawing a hexagon is very simple; all you need is a compass and a ruler.

The step-by-step instructions will look like this:

a straight line is drawn and a dot is placed on it;
a circle is constructed from this point (it is its center);
From the intersections of the circle with the line, two more of the same are built, they should converge in the center.
after this, all points on the first circle are sequentially connected by segments.

If you wish, you can do without a line by drawing five circles of equal radius.

The figure thus obtained will be a regular hexagon, and this can be proven below.

Drawing a tetrahedral prism

A tetrahedral prism is built according to the same plan as a cube, so it is logical to first master drawing this figure. Both of them are simple geometric solids with straight edges. However, if all the faces of a cube are squares, then the squares of a prism are only the bases, and the side faces are rectangles.

The object is drawn in exactly the same way as a cube, the length of which then increases horizontally or vertically (depending on the position of the object).

As a rule, the length increases by one and a half times, but this depends on how many times the height of the figure exceeds the width of the base of the prism.

First you need to draw the general dimensions of the figure on a sheet of paper using light pencil lines.

Then you need to find where the front vertical edge will be and draw a line on which to mark the height of the body. After this, the slopes of the ribs are outlined. Then all invisible edges are drawn.

Properties are simple and interesting

To understand the properties of a regular hexagon, it makes sense to divide it into six triangles:

This will help in the future to more clearly display its properties, the main of which are:

circumscribed circle diameter;
diameter of the inscribed circle;
square;
perimeter.

Circumscribed circle and constructability

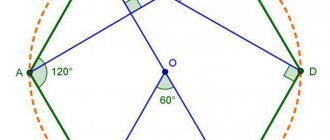
A circle can be described around a hexagon, and only one. Since this figure is regular, you can do it quite simply: draw a bisector from two adjacent corners inside. They intersect at point O, and together with the side between them form a triangle.

The angles between the hexagon side and the bisectors will be 60°, so we can definitely say that a triangle, for example, AOB, is isosceles. And since the third angle will also be equal to 60°, it is also equilateral. It follows that the segments OA and OB are equal, which means they can serve as the radius of a circle.

After this, you can move to the next side, and also draw a bisector from the angle at point C. You will get another equilateral triangle, with side AB being common to both of them, and OS being the next radius through which the same circle goes. There will be six such triangles in total, and they will have a common vertex at point O. It turns out that it will be possible to describe a circle, and there is only one of it, and its radius is equal to the side of the hexagon:

R=a.

That is why it is possible to construct this figure using a compass and ruler.

Well, the area of this circle will be standard:

S=πR²

Inscribed circle

The center of the circumcircle will coincide with the center of the inscribed circle. To verify this, you can draw perpendiculars from point O to the sides of the hexagon. They will be the heights of the triangles that make up the hexagon. And in an isosceles triangle, the height is the median with respect to the side on which it rests. Thus, this height is nothing more than the perpendicular bisector, which is the radius of the inscribed circle.

The height of an equilateral triangle is calculated simply:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

And since R=a and r=h, it turns out that

r=R(√3)/2.

Thus, the incircle passes through the centers of the sides of a regular hexagon.

Its area will be:

S=3πa²/4,

that is, three quarters of what is described.

Perimeter and area

Everything is clear with the perimeter, it is the sum of the lengths of the sides:

P=6a , or P=6R

But the area will be equal to the sum of all six triangles into which the hexagon can be divided. Since the area of a triangle is calculated as half the product of the base and the height, then:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 or

S=3R²(√3)/2

Those who wish to calculate this area through the radius of the inscribed circle can do this:

Entertaining constructions

You can fit a triangle into a hexagon, the sides of which will connect the vertices through one:

There will be two of them in total, and their overlap will give the Star of David. Each of these triangles is equilateral. This is not difficult to verify. If you look at the AC side, it belongs to two triangles at once - BAC and AEC. If in the first of them AB = BC, and the angle between them is 120°, then each of the remaining ones will be 30°. From this we can draw logical conclusions:

The height ABC from vertex B will be equal to half the side of the hexagon, since sin30°=1/2. Those who want to verify this can be advised to recalculate using the Pythagorean theorem; it fits here perfectly.
Side AC will be equal to two radii of the inscribed circle, which is again calculated using the same theorem. That is, AC=2(a(√3)/2)=a(√3).
Triangles ABC, CDE and AEF are equal in two sides and the angle between them, and from this it follows that the sides AC, CE and EA are equal.

Intersecting each other, the triangles form a new hexagon, and it is also regular. This is proven simply:

Angle ABF is equal to angle BAC. Thus, the resulting triangle with base AB and an unnamed vertex opposite it is isosceles.
All the same triangles, the base of which is the side of the hexagon, are equal along the side and the adjacent angles.
The triangles at the vertices of the hexagon are equilateral and equal, which follows from the previous paragraph.
The angles of the newly formed hexagon are 360-120-60-60=120°.

Method for drawing a hexagon without a compass

Building a regular hexagon without a compass requires the presence of a ruler - a special tool in the form of a ruler, inside the body of which there is a massive shaft with rubber elements that prevent slipping. It is designed for the rapid production of parallel lines, ensuring high accuracy of construction. The quality of drawing in this method depends entirely on the accuracy of the 60° angle in a factory-made square and the graduation of the ruler scale.

The construction method looks like this:

The second way to draw a hexagon with a compass: 1,2,3,4,5,6 - corners, 0 - center, D - radius of the hexagon.

a square is applied to one side of the segment - the short side is aligned with the line, an angle of 60° is adjacent to the end of the segment from the inside, a line of arbitrary size is drawn along the hypotenuse of the square, which is subsequently adjusted using the scale of the ruler;
a line is drawn on the sheet/blank - its length is equal to two dimensions of the side of the polygon, the edges automatically become the centers of the polyhedron;
the operation is repeated when turning the square - the 60° angle moves to the opposite side of the segment, the center of rotation is the long leg of the square;
turning the square - now the short leg of the square becomes the center of rotation, two more faces are drawn;
clarification of the sizes of the sides - on the four resulting sides of the polygon, their exact size is plotted along a ruler;
construction of the two remaining sides - they are located parallel to the line from which the drawing began, drawn along a ruler, then their size is specified;
parallelism control - the gauge scale is aligned with the line from which the construction of the figure began, then the tool moves up/down to ensure that two opposite edges are parallel to each other, with this segment

In this case, the hexagon takes longer to draw than in the first method. However, this way you can construct the necessary figure, in the absence of a compass, using a square. The technology is based on the parallelism of opposite sides of a regular hexagon, identical internal angles of 60°.

The industry produces squares with both sharp corners, convenient for this method, and with rounded ones.

The third way to draw a hexagon with a compass: a is the diameter, b is the side of the hexagon.

In the latter case, it is more convenient to slightly change the technology:

after drawing the central segment, the crossbar is aligned along it;
the tool rolls down by an arbitrary amount;
the short hypotenuse of the square is combined with the ruler of the line, and not with the central segment;
the rounded edge of the instrument is not involved in the construction; the line is drawn along the solid part of the hypotenuse.

The operation is repeated on the opposite side of the segment, after which the crossbar turns 180°, again aligns with the center line, and rolls up to construct the other two sides of the polyhedron.

These are standard methods for drawing an equilateral polygon with six corners and faces. They are convenient for cutting workpieces of any size from different materials, using standard drawings on whatman paper. Both methods have exclusively applied significance, since in professional graphic editors (AutoCAD, Compass-3D) such figures are created automatically by setting the necessary parameters.

Drawing Basics

Construction

Mechanical Engineering

Construction of a regular hexagon inscribed in a circle. The construction of a hexagon is based on the fact that its side is equal to the radius of the circumscribed circle. Therefore, to construct it, it is enough to divide the circle into six equal parts and connect the found points to each other (Fig. 60, a).

A regular hexagon can be built using a straight edge and a 30X60° square. To carry out this construction, we take the horizontal diameter of the circle as the bisector of angles 1 and 4 (Fig. 60, b), construct sides 1 -6, 4-3, 4-5 and 7-2, after which we draw sides 5-6 and 3- 2.

Construction of an equilateral triangle inscribed in a circle. The vertices of such a triangle can be constructed using a compass and a square with angles of 30 and 60° or just one compass.

Let's consider two ways to construct an equilateral triangle inscribed in a circle.

The first method (Fig. 61,a) is based on the fact that all three angles of the triangle 7, 2, 3 contain 60°, and the vertical line drawn through point 7 is both the height and the bisector of angle 1. Since the angle is 0- 1-2 is equal to 30°, then to find the side

1-2, it is enough to construct an angle of 30° from point 1 and side 0-1. To do this, install the crossbar and square as shown in the figure, draw line 1-2, which will be one of the sides of the desired triangle. To construct side 2-3, set the crossbar in the position shown by the dashed lines, and draw a straight line through point 2, which will determine the third vertex of the triangle.

From theory to practice

The properties of the hexagon are very actively used both in nature and in various fields of human activity. First of all, this applies to bolts and nuts - the heads of the first and second are nothing more than a regular hexagon, if you do not take the chamfers into account. The size of the wrenches corresponds to the diameter of the inscribed circle - that is, the distance between opposite edges.

Hexagonal tiles have also found their use. It is much less common than the quadrangular one, but it is more convenient to lay it: three tiles meet at one point, rather than four. The compositions can turn out to be very interesting:

Concrete tiles for paving are also produced.

The prevalence of hexagons in nature is simply explained. Thus, it is easiest to fit circles and balls tightly on a plane if they have the same diameter. Because of this, honeycombs have this shape.

How to build and draw a regular pentagon around a circle

A regular pentagon is a geometric figure that is formed by the intersection of five straight lines, creating five equal angles. This figure is called the Pentagon. The work of artists is closely related to the pentagon - their drawings are based on regular geometric shapes. To do this, you need to know how to quickly build a Pentagon.

Why is this figure interesting? of the United States Department of Defense has the shape of a Pentagon . This can be seen in photographs taken from a flight altitude. There are no crystals or stones in nature whose shape resembles a pentagon. Only in this figure the number of faces coincides with the number of diagonals.

How to correctly depict a hexagonal prism?

A hexagonal prism is much more difficult to construct. You can follow the principle of constructing a tetrahedral prism, where the base is first designated, and then the side faces are completed. You can build differently. In order to correctly construct a hexagonal prism, we must construct a tetrahedral one.

In doing so, we divide the front face in half, creating additional faces. This method is more difficult, since a mistake at the first stage can spoil the final result. We build a hexagonal prism using knowledge about the opening of ellipses, which contributes to the correct determination of the dimensions of the faces. Like any object, the volume of a prism is created using chiaroscuro. We start shading evenly, after which we add tone in the darkest areas.

Parameters of a regular pentagon

A rectangular pentagon, like every figure in geometry, has its own parameters. Knowing the necessary formulas, you can calculate these parameters, which will facilitate the process of building a pentagon. Calculation methods and formulas:

the sum of all angles in polygons is 360 degrees. In a regular pentagon, all angles are equal, respectively, the central angle is found in this way: 360/5 = 72 degrees;
the internal angle is found in this way: 180*(n -2)/ n = 180*(5−2)/5 = 108 degrees. Sum of all interior angles: 108*5 = 540 degrees.

The side of the pentagon is found using the parameters that are already given in the problem statement:

if a circle is circumscribed around a pentagon and its radius is known, the side is found using the following formula: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1.1756*R.
If the radius of the circle inscribed in the pentagon is known, then the formula for calculating the side of the polygon is: 2*r*tg (α/2) = 2*r*tg (α/2) = 1.453*r.
Given the known size of the pentagon's diagonal, its side is calculated as follows: a = D/1.618.

The area of the pentagon , as well as its side, depends on the parameters already found:

Using the known radius of the inscribed circle, the area is found as follows: S = (n*a*r)/2 = 2.5*a*r.
a circle circumscribed around a pentagon allows you to find the area using the following formula: S = (n*R2*sin α)/2 = 2.3776*R2.
depending on the side of the pentagon: S = (5*a2*tg 54°)/4 = 1.7205* a2.

This website is using a security service to protect itself from online attacks.

This process is automatic, you will be redirected to the requested URL once the validation process is complete.

In the broadest sense, a hexagon is a polygon with six corners. A regular hexagon has equal angles and sides. You can draw such a hexagon using a tape measure and a protractor, a rough hexagon using a round object and a ruler, or an even rougher hexagon using intuition and a pencil. If you want to know how to draw a hexagon in different ways, just read on.

Is there a pencil near you? Take a look at its cross-section - it is a regular hexagon or, as it is also called, a hexagon. The cross-section of a nut, a field of hexagonal chess, the crystal lattice of some complex carbon molecules (for example, graphite), a snowflake, a honeycomb and other objects also have this shape. A giant regular hexagon was recently discovered in Saturn's atmosphere. Doesn’t it seem strange that nature so often uses structures of this particular form for its creations? Let's take a closer look at this figure.

The length of its sides corresponds to the radius of the circumscribed circle. Of all the geometric shapes, only the regular hexagon has this property.
The angles are equal to each other, and each measure is 120°.
The perimeter of a hexagon can be found using the formula P=6*R, if the radius of the circle described around it is known, or P=4*√(3)*r, if the circle is inscribed in it. R and r are the radii of the circumscribed and inscribed circle.
The area occupied by a regular hexagon is determined as follows: S=(3*√(3)*R 2 )/2. If the radius is unknown, substitute the length of one of the sides - as is known, it corresponds to the length of the radius of the circumscribed circle.

Building the Pentagon

You can construct a regular pentagon using a ruler and compass, based on a circle inscribed in it or one of the sides.

How to draw a pentagon based on an inscribed circle? To do this, you need to stock up on compasses and a ruler and take the following steps:

First you need to draw a circle with center O, and then select a point on it, A - the vertex of the pentagon. A segment is drawn from the center to the top.
Then a segment perpendicular to straight line OA is constructed, which also passes through O, the center of the circle. Its intersection with the circle is designated by point B. The segment O.B. is divided in half by point C.
Point C will become the center of a new circle passing through A. Point D is its intersection with straight line OB within the boundaries of the first figure.
After this, a third circle is drawn through D, the center of which is point A. It intersects with the first figure at two points, they must be designated by the letters E and F.
The next circle has its center at point E and passes through A, and its intersection with the original is at a new point G.
The last circle in this figure is drawn through point A with center F. At its intersection with the initial circle, point H is placed.
On the first circle, after all the steps taken, five points appeared that need to be connected by segments. Thus, a regular pentagon AE G H F was obtained.

How to construct a regular pentagon in another way? Using a ruler and compass, you can build a pentagon a little faster. To do this you need:

First, you need to use a compass to draw a circle whose center is point O.
The radius OA is drawn - a segment that is plotted on the circle. It is divided in half by point B.
A segment OS is drawn perpendicular to the radius OA, points B and C are connected by a straight line.
The next step is to plot the length of the segment BC using a compass on the center line. Point D appears perpendicular to segment OA. Points B and D are connected to form a new segment.
In order to obtain the size of the side of the pentagon, it is necessary to connect points C and D.
D is transferred to the circle using a compass and is designated by point E. By connecting E and C, you can get the first side of a regular pentagon. By following these instructions, you can learn how to quickly build a pentagon with equal sides, continuing the construction of its remaining sides like the first.

Hexagonal prism

The basis for constructing a hexagonal prism is a tetrahedral one. The front surface is divided in half vertically and horizontally, taking into account perspective if the body is depicted from foreshortening. Then we inscribe an ellipse into the surface. The horizontal axis intersecting the surface is divided in half again, taking into account perspective. We put points at the intersections of the resulting verticals with the circle. We connect them to each other and to the corners.

The exact same hexagon needs to be drawn on the back side of the tetrahedral prism, and then connected to the first hexagon drawn. Thus, we will get a hexagonal prism inscribed in a tetrahedral one.

To show the volume of your prism, you need to indicate chiaroscuro. First of all, you need to shade the surfaces in the shadow and those on which the shadow falls. After this, you need to work on the most illuminated surfaces.

Interesting Facts

In a pentagon with equal sides, the diagonals are equal and form a five-pointed star, which is called a pentagram. The golden ratio is the ratio of the diagonal to the side of the pentagon.

The pentagon is unsuitable for completely filling the plane. Using any material in this form leaves gaps or creates overlaps. Although natural crystals of this form do not exist in nature, when ice forms on the surface of smooth copper products, molecules in the form of a pentagon appear, which are connected in chains.

The easiest way to get a regular pentagon from a strip of paper is to tie it in a knot and press it down a little. This method is useful for parents of preschool children who want to teach their kids to recognize geometric shapes.

Creating a single hexagon in C# using DrawPolygon

This makes a triangle, but I can't figure out the x and y values for a hexagon, sounds like a simple question but my brain just isn't working correctly today, Below is the array for a hexagon, I just can't figure out the values.

Any help would be greatly appreciated!

1 answer

Mapping a variable to the size of a hexagon using geom_hex

Does anyone know if it is possible to plot the size of a hexagon using ggplot? Size is listed as an argument in the geom_hex documentation, but there are no size matching examples in stat_hexbin, so it just relates to the cell size. Take for example: ggplot(economics, aes(x=uempmed.

So I've seen solutions for how to crop UIImages into certain shapes, but what about a hexagon? Thought: Subclass UIImage, change the drawRect method to only draw certain sections? EDIT: To be more precise, I'm hoping to keep the borders of the image the same, but do.

Since I already wrote a comment, I think I should demonstrate this in some real code.

I've created a WinForms application with a Panel object that I can draw on. Then I overridden the Paint event to draw the hexagon.

This then attracts

As I said, the key is to treat the hexagon as a "discrete" circle. All points are calculated as being on the outside of a perfect circle, which are then connected by a straight line. With this technique you can create all regular n-Point shapes (like a 5-regular pentagon ;))

So you simply "inscribe" 6 points in a circle to get your hexagon, as shown in this diagram with the correct 5-point shape:

Then remember that you can calculate the (x,y) coordinates of a point given its polar coordinates (r, phi) as follows

To which you can also add offset, which in my case is the center of the frame in which I am drawing.

I'M GROWING a site for children and their parents

Latest events

Halloween coloring pages for boys

In Russia, the celebration of Halloween is not connected with anything. This is most likely a tribute to fashion than the traditions of our ancestors. An interesting, vibrant show, the meaning and origin of which many people don’t even know.

Collection of Halloween coloring pages

Halloween is coming soon. Holiday horror story, holiday scarecrow. It’s no wonder that children from all over the world love him so much.

I already posted a selection of Halloween coloring pages on the site.

Autumn. Trees and leaves

What do trees look like in autumn? Look at the pictures and color the autumn leaves.

Who are Gummi Bears?

Watch this animated series about Gummi Bears with your children, then download coloring pages and color the characters.

Several coloring pages for little ones

Very simple coloring books with large details for the youngest artists.

Autumn mood. Coloring pages

Golden autumn is in full swing. This year it is as late as ever in our area and dazzlingly beautiful.

Stories about autumn. Reading and coloring pictures

What is autumn? What is the weather like in autumn? What do birds do in the fall? Ask these and other questions about autumn to your baby.

mercury13_kiev

Yes, hexagonal meshes are not just for bees.

This house is called Queen B

, and is designed to protect people from weather and radiation on Mars. Here are the characteristics of this house stated by the authors.

A full kitchen, two bathrooms, two bedrooms, a garden, a 3D printing laboratory, a recreation room, a laundry room and a decompression room combined with a locker room.
Heat-saving design with a durable roof that protects against debris.
Depleted uranium panels that bring radiation to a safe level.
Aesthetic appearance attracts the press, helps publicize the mission and recruit volunteers.

This last point is important for games: hexagonal buildings attract press.

How to build a regular hexagon without a compass