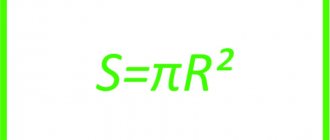Как нарисовать шестиугольник с помощью линейки

Дрель аккумуляторная HAMMER ACD14BS

4699 ₽ Подробнее

XXI CENTURY Конфетка Помадка Душистая вода 266 ₽ Подробнее

HAMMER

Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.

Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.

В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

чертится прямая линия и на ней ставится точка;
из этой точки строится окружность (она является ее центром);
из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
после этого отрезками последовательно соединяются все точки на первой окружности.

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Рисуем четырехгранную призму

Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они — это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты — это только основания, а боковые грани — прямоугольники.

Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).

Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.

Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.

Затем нужно найти, где будет находиться переднее вертикальное ребро, и провести линию, на которой отложить высоту тела. После этого намечаются наклоны ребер. Затем прорисовываются все невидимые грани.

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

диаметр описанной окружности;
диаметр вписанной окружности;
площадь;
периметр.

Описанная окружность и возможность построения

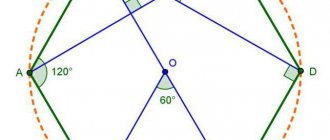
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком

Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.

Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

после вычерчивания центрального отрезка по нему выравнивается рейсшина;
инструмент откатывается вниз на произвольную величину;
короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

Основы черчения

Строительное

Машиностроительное

Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Как построить и нарисовать правильный пятиугольник по окружности

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Как правильно изобразить шестигранную призму?

Шестигранная призма строится уже значительно сложнее. Можно идти по принципу построения четырехгранной призмы, где сначала обозначается основа, а затем достраиваются боковые грани. Можно строить иначе. Для того, чтобы правильно построить шестигранную призму, мы должны построить четырехгранную.

При этом мы делим переднюю грань пополам, создавая дополнительные грани. Этот способ сложнее, так как ошибка на первом этапе может испортить итоговый результат. Шестигранную призму мы строим с применениями знаний о раскрытии эллипсов, что способствует правильному определению размеров граней. Как и любой предмет, объемность призмы создается с помощью светотени. Начинаем штриховку равномерно, после чего добираем тон в самых темных участках.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

This website is using a security service to protect itself from online attacks.

This process is automatic, you will be redirected to the requested URL once the validation process is complete.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
Углы равны между собой, и величина каждого составляет 120°.
Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Шестигранная призма

Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.

Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.

Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Создание одного шестиугольника в C# с помощью DrawPolygon

Это делает треугольник, но я не могу понять значения x и y для шестиугольника, звучит как простой вопрос, но мой мозг просто не работает правильно сегодня, Ниже приведен массив для шестиугольника, я просто не могу понять значения.

Любая помощь была бы большой благодарностью!

1 ответ

Сопоставление переменной с размером шестиугольника с помощью geom_hex

Кто-нибудь знает, можно ли сопоставить размер шестиугольника с помощью ggplot? Размер указан в качестве аргумента в документации geom_hex , но в stat_hexbin нет примеров сопоставления размеров , так что это просто связано с размером ячейки. Взять для примера: ggplot(economics, aes(x=uempmed.

Итак, я видел решения для того, как обрезать UIImages в определенные формы, но как насчет шестиугольника ? Мысль: подкласс UIImage, изменить метод drawRect, чтобы рисовать только определенные разделы? EDIT: если быть более точным, я надеюсь сохранить границы изображения одинаковыми, но сделать.

Поскольку я уже написал комментарий, я думаю, что должен продемонстрировать это в каком-то реальном коде.

Я создал приложение WinForms с объектом Panel , на котором я могу рисовать. Затем я переопределил событие Paint , чтобы нарисовать шестиугольник.

Это затем привлекает

Как я уже сказал, ключ состоит в том, чтобы рассматривать шестиугольник как круг «discrete». Все точки вычисляются как находящиеся на внешней части идеального круга, которые затем соединяются прямой линией. С помощью этой техники вы можете создать все правильные фигуры n-Point (например, пятиугольник в виде фигуры 5-regular ;))

Итак, вы просто «inscribe» 6 точек в круге, чтобы получить свой шестиугольник, как показано на этой диаграмме с правильной 5-точечной формой:

Затем помните, что вы можете вычислить координаты (x,y) точки с учетом ее полярных координат (r, phi) следующим образом

К которому вы также можете добавить смещение , которое в моем случае является центром кадра, в котором я рисую.

Я РАСТУСайт для детей и их родителей

Последние события

Раскраски к Хеллоуину для мальчиков

В России – празднование Хэллоуина ни с чем не связано. Это, скорее всего дань моде, чем традиции предков. Интересное яркое шоу, о значении и первоисточнике которого многие даже не догадываются.

Коллекция раскрасок к Хеллоуину

Скоро Хеллоуин. Праздник страшилка, праздник пугалка. Не зря его так любят дети всех стран.

На сайте я уже как-то выкладывала подборку раскрасок к Хеллоуину.

Осень. Деревья и листья

Как выглядят деревья осенью? Рассмотрите картинки и раскрасьте осенние листики.

Кто такие мишки Гамми?

Посмотрите с детьми этот мультсериал про мишек Гамми, затем скачайте раскраски и раскрасьте героев.

Несколько раскрасок для самых маленьких

Совсем простенькие раскраски с крупными деталями для самых маленьких художников.

Осеннее настроение. Раскраски

В разгаре золотая осень. В этом году она в наших краях как никогда поздняя и ослепительно красивая.

Рассказы про осень. Читаем и раскрашиваем картинки

Что такое осень? Какая осенью погода? Что делают птицы осенью? Задайте эти и другие вопросы про осень своему малышу.

mercury13_kiev

Да, шестиугольные сетки не только для пчёл.

Этот дом называется Queen B

, и создан, чтобы защищать людей от погоды и излучения на Марсе. Вот заявленные авторами характеристики этого дома.

Полноценная кухня, две ванных, две спальни, садик, лаборатория 3D-печати, комната отдыха, прачечная и совмещённая с раздевалкой декомпрессионная.
Теплосберегающая конструкция с прочной крышей, защищающей от обломков.
Панели из обеднённого урана, доводящие радиацию до безопасного уровня.
Эстетичный вид привлекает прессу, помогает освещать миссию и вербовать добровольцев.

Последний пункт важен для игр: шестиугольные постройки привлекают прессу.

Правильный шестиугольник как построить без циркуля