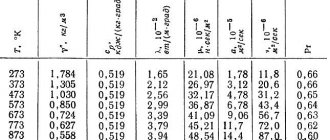
Thermal conductivity coefficient of stainless steel
The thermal conductivity of stainless steel is relatively low compared to other alloys. The material is widely used in aggressive environments and as elements for architectural structures. It is often used for facades of buildings, furnaces and conveyors in production. The advantage of low thermal conductivity is high energy efficiency and stability.
If the thermal conductivity coefficient of carbon type steel is within 45 W/(m·K), then the thermal conductivity coefficient of stainless steel is only about 15 W/(m·K). The ability of an alloy to transfer heat is influenced by its composition, as well as the surrounding temperature environment. When purchasing stainless steel products, it is very important to pay due attention to this criterion.
Thermal conductivity of aluminum and steel
If you compare the thermal conductivity of aluminum and steel, it is important to start from the conditions of their planned operation. The thermal conductivity of aluminum at typical room temperature is about 236 W/(m deg). In view of this, the material is often used for the production of radiators and heat sinks.
Aluminum melts at a temperature of 660 °C, and important properties of the material are significantly lost. The indicators largely depend on physical parameters, for example, density. Today, alloys of aluminum with copper, silicon and zinc are in demand.
According to technological features they are divided into:
- Foundries;
- Deformable.
Thermal conductivity of cast iron and steel
Both materials are an alloy of carbon and iron. They are widely used both in industry and in everyday life. Steel is characterized by increased hardness and strength, while cast iron is lightweight and has a lower melting point. Steel is easier to process due to its lower carbon content (compared to cast iron).
The thermal conductivity of cast iron and steel is very important and almost every buyer pays great attention to this indicator. The thermal conductivity of alloys, unlike heat capacity indicators, cannot be determined using the mixing rule. But it is only possible to establish the influence of individual elements on the thermal conductivity of cast iron only approximately.
Need high-quality steel?
Choose a material with suitable properties on our website and place your order! Our assortment includes materials for a wide variety of purposes!
conclusions
When the task is to buy stainless steel and the thermal conductivity of the material is of serious importance, it is important to pay attention to its other characteristics. It is necessary to take into account the composition of the alloy, the temperature environment at the place of operation and other equally important components. Our company’s specialists are always ready to help you with the choice of steel, providing personal advice.
The low thermal conductivity of stainless steel can be a significant, if not the main, advantage of the material. When planning a purchase, pay attention to all specified technical indicators. And our employees will always be happy to give you comprehensive answers to additional questions.
has been successfully operating and developing on the Ukrainian rolled metal market since 2003. In our assortment of items there will certainly be an option that meets your important criteria for your needs. We value the choice of our customers and exercise high quality control of the goods!
Source
Importance in everyday life and production
Why is it important to consider thermal conductivity? A similar value is indicated in various tables for each metal and is taken into account in the following cases:
- In the manufacture of various heat exchangers. Heat is one of the important carriers of energy. It is used to provide comfortable living conditions in residential and other premises. When creating heating radiators and boilers, it is important to ensure rapid and complete heat transfer from the coolant to the end consumer.
- In the manufacture of outlet elements. You can often encounter a situation where you need to remove heat rather than supply it. An example is the case of heat removal from the cutting edge of a tool or gear teeth. To ensure that the metal does not lose its basic performance qualities, rapid removal of thermal energy is ensured.
- When creating insulating layers. In some cases, the material should not conduct thermal energy transfer. For such operating conditions, a metal is selected that has a low heat conductivity coefficient.
Why calculate heat transfer
Calculating the heat transfer coefficient for steel pipes and products made from them will help determine how many kilocalories or Joules of internal coolant they are capable of transferring to the atmosphere. When designing heating, after such a calculation it is easy to calculate the required diameter of the steel pipe. If everything is done correctly, the efficiency of the heaters will be maximum.
Sometimes exactly the same calculation of the heat transfer of steel pipes is needed for the opposite - to select an insulating material that can prevent losses. It all depends on the purpose and operating conditions of the pipeline under study.
In a simplified form, the formula for thermal conductivity looks like this:
For those who have forgotten the 7th grade physics course, let us recall the meanings of these symbols:
- k is the heat transfer coefficient of pipe steel. It depends on the characteristics of the material, wall thickness and is tied to the amount of thermal pressure.
- F – pipe surface area. If several pipeline lines are connected at once, then the total surface area is taken into account.
- Δt – thermal pressure, taking into account the temperature difference between the atmosphere and the coolant.
Simply put, the heat transfer of a steel pipe directly depends on its size and degree of heating compared to the external environment. The higher these indicators, the more thermal energy it will transfer.
The heat transfer of a steel pipe largely depends on its thickness. Thermal pressure is also calculated for each specific case. Here it is necessary to additionally take into account the average temperature of hot water at the inlet and outlet of the heating device (the heat transfer coefficient of water differs from the same indicator for steel). For preliminary calculations, Δt according to SNiP is taken equal to 55° C.
It is more convenient to carry out calculations for one conventional meter of pipe of the selected diameter. Then the finished result can simply be multiplied by the total length of the heating equipment. For different pipe sizes, heat transfer is determined separately.
3.7. Thermal conductivity
The thermal conductivity coefficient λ denotes the amount of heat transferred per unit time through a unit surface with a unit temperature gradient, i.e., with a temperature difference of one degree per unit wall length normal to the heat flow.
Thermal conductivity coefficient dimension: W/(m K).
In table 3.7.1 shows the thermal conductivity coefficients of metals and alloys.
For each value of λ, the temperature to which this value corresponds is indicated. In cases where such an indication is absent, the data refers to room temperature.
Table 3.7.1
Thermal conductivity coefficients of metals and alloys
The composition of the alloys is indicated in mass fractions (except where otherwise specified).
| Metal or alloy, mass. % | T, °С | λ, W/(m K) |
| Aluminum 99 | 18 | 211 |
| 30 | 208,1 | |
| 100 | 205,2 | |
| 400 | 318,2 | |
| 600 | 422,9 | |
| Bismuth | –186 | 10,47 |
| –77 | 10,76 | |
| 0 | 7,411 | |
| 100 | 6,866 | |
| 96 Bi + 3.5 Pb (vol.) | 44 | 5,401 |
| 90 Bi + 3.5 Sn (vol.) | 44 | 5,401 |
| 80 Bi + 20 Sb | 0 | 6,364 |
| 100 | 8,583 | |
| 50 Bi + 50 Sn | 12,5 | 23,45 |
| 50 Bi + 25 Pb + 25 Sn | 20 | 16,24 |
| 48 Bi + 26 Pb + 13 Sn + 13 Cd | 7 | 13,36 |
| Tungsten | 0 | 160,4 |
| 2227 | 148,2 | |
| Iron | ||
| forged pure | 0 | 59,45 |
| 100 | 56,94 | |
| 99.92 (armco) | 20 | 73,27 |
| 100 | 67,41 | |
| Gold | 0 | 311,5 |
| 97 | 312,3 | |
| 90 Au + 10 Pd | 25 | 97,97 |
| 50 Au + 50 Pd | 25 | 36,01 |
| Iridium | 17 | 59,03 |
| Cadmium | 0 | 92,65 |
| 100 | 85,62 | |
| Potassium | 5 | 97,97 |
| 20,7 | 97,13 | |
| 57,6 | 90,85 | |
| 62.9 K + 37.1 Na | 6,0 | 22,99 |
| 42,9 | 25,92 | |
| Cobalt (97.12 Co + 0.24 C + 1.4 Fe + 1.1 Ni + 0.14 Si) | 30 | 487,8 |
| Brass | ||
| red | 0 | 103 |
| 100 | 118,5 | |
| yellow | 0 | 85,45 |
| 100 | 106,3 | |
| Lithium | 0 | 71,18 |
| 101,3 | 75,36 | |
| Magnesium | 0–100 | 157,4 |
| 92 Mg + 8 Al | 20–200 | 62,8–79,55 |
| 92 Mg + 8 Cu | 20–200 | 125,6–132,3 |
| 88 Mg + 10 Al + 2 Si | 20–200 | 121,4–133,1 |
| Manganese | 18 | 21,77 |
| Copper | –183 | 465,2 |
| 0 | 385,2 | |
| 100 | 385,2 | |
| 99.37 Cu + 0.63 P | 30 | 104,7 |
| 98.02 Cu + 1.98 P | 30 | 52,34 |
| 96 Cu + 3 Si + 1 Mn (everdure) | 20 | 33,08 |
| 84 Cu + 4 Ni + 12 Mn (manganin) | 18 | 21,73 |
| 100 | 26,42 | |
| 60 Cu + 40 Ni | 18 | 22,61 |
| 100 | 26,8 | |
| 54 Cu + 46 Ni | 18 | 20,26 |
| 89 Cu + 11 Zn | 18 | 115,1 |
| 87 Cu + 13 Zn | 18 | 126 |
| 82 Cu + 18 Zn | 18 | 131 |
| 68 Cu + 32 Zn | 18 | 108,9 |
| 62 Cu + 22 Zn + 15 Ni | 18 | |
| 52 Cu + 26 Zn + 22 Ni | 0 | 29,31 |
| 100 | 36,43 | |
| 95 Cu + 5 Al (aluminum bronze) | 20 | 82,48 |
| 90 Cu + 10 Sn | 20 | 41,87 |
| 75 Cu + 25 Sn (tin bronze) | 20 | 25,54 |
| 92.8 Cu + 5 Sn + 2 Zn + 0.15 P (phosphor bronze) | 20 | 79,13 |
| Molybdenum | 17 | 144,9 |
| Sodium | 5,7 | 134,4 |
| 21,2 | 132,7 | |
| 88,1 | 120,6 | |
| Nickel 99 | –160 | 54,01 |
| 18 | 58,62 | |
| Ni + (2÷3) Co | 300 | 52,75 |
| 79.5 Ni + 13 Cr + 6.5 Fe (niconel) | 70 | 15,07 |
| Tin | –170 | 81,64 |
| 0 | 64,06 | |
| 100 | 59,45 | |
| 91 Sn + 8.9 Zn | 44 | 65,73 |
| Palladium | 100 | 76,2 |
| 90 Pd + 10 Pt | 25 | 56,1 |
| 50 Pd + 50 Pt | 25 | 36,84 |
| 90 Pd + 10 Ag | 25 | 47,73 |
| 50 Pd + 50 Ag | 25 | 31,82 |
| Platinum | –252,8 | 389,4 |
| –183 | 76,2 | |
| 0–200 | 69,92 | |
| 90 Pt + 10 Ir | 17 | 30,98 |
| 90 Pt + 10 Rh | 17 | 30,14 |
| 90 Pt + 10 Pd | 25 | 43,12 |
| Rhodium | 17 | 87,92 |
| Mercury | ||
| hard | –269,3 | 167,5 |
| –44,2 | 27,8 | |
| liquid | 0 | 8,081 |
| 50 | 8,75 | |
| Lead | 18 | 34,62 |
| 100 | 34,12 | |
| Silver 99.9 | –160 | 417,8 |
| 0 | 458,9 | |
| 10–97 | 403,2 | |
| Silver 99.98 | 18 | 421,2 |
| 100 | 415,3 | |
| 90 Ag + 10 Pd | 25 | 141,1 |
| 90 Ag + 10 Pt | 25 | 97,97 |
| 70 Ag + 30 Pt | 25 | 30,98 |
| Steel | See table. 3.7.2 | |
| Antimony | 0 | 18,42 |
| 0–30 | 17,58 | |
| 100 | 16,75 | |
| 70 Sb + 30 Bi | 0 | 9,797 |
| 100 | 11,76 | |
| 66.7 Sb + 33.3 Cd | 0 | 1,252 |
| 50 Sb + 50 Cd | 0 | 2,173 |
| Tantalum | 17 | 54,43 |
| 1827 | 82,9 | |
| Zinc | –170 | 117,2 |
| 18 | 111 | |
| 100 | 109,7 | |
| 70 Zn + 30 Sn | 44 | 93,78 |
| Cast iron | 18 | 45,64 |
| 100 | 45,22 | |
| Metal or alloy, mass. % | T, °С | λ, W/(m K) |
In table 3.7.2–3.7.7 show the thermal conductivity coefficients of some steels, pure substances in the solid state, thermal insulation, construction and some other materials, liquid metal coolants, pure organic liquids and refrigerants in the liquid state.
Table 3.7.2
Thermal conductivity coefficients λ (W/(m K)) of some steels
| Steel group | Temperature, °C | |||||||
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | |
| Carbon: grade 15 | 54,4 | 50,2 | 46,1 | 41,9 | 37,7 | 33,5 | ||
| mark 30 | 50,2 | 46,1 | 41,9 | 37,7 | 33,5 | 29,3 | ||
| Molybdenum | 41,9 | |||||||
| Chrome | 22,4 | 21,2 | 23,5 | 22 | ||||
| Chrome-molybdenum: Х10С2М (ЭИ107) | 18,4 | 0 | 21,7 | 24,7 | 22 | |||
| 12 XM | 37,7 | 35,6 | 33,5 | |||||
| Chrome-nickel | 16,9 | 19,2 | 21,5 | 24,4 | 26,7 | 29,7 | 32,6 | 36,1 |
| Chrome-nickel-tungsten | 15,5 | 0 | 18,1 | 21,2 | 22 | |||
Table 3.7.3
Thermal conductivity coefficients of some pure substances in the solid state
| Name | Formula | T, °С | λ, W/(m K) |
| Aluminum oxide: | Al2O3 | ||
| powder | 46,8 | 0,678 | |
| fused | 650–1350 | 3,349 | |
| Graphite (density 1580 kg/m3): | WITH | ||
| axes | 50 | 44,17 | |
| + axes | 142 | 17,84 | |
| 555 | 116,8 | ||
| Graphite (powder, density 700 kg/m3) | WITH | 40 | 1,193 |
| Cadmium oxide (pressed powder) | CdO | 46,5 | 0,682 |
| Potassium iodide | KI | 0 | 5,024 |
| Potassium chloride | KCl | 0 | 6,95 |
| Cobalt(III) oxide (pressed powder) | Co2O3 | 48,5 | 0,419 |
| Silicon carbide (carborundum) | SiC | 650–1350 | 15,57 |
| Silicon dioxide (quartz): | SiO2 | ||
| axes | 0 | 13,61 | |
| 100 | 9,002 | ||
| + axes | 0 | 7,247 | |
| 100 | 5,581 | ||
| Magnesium oxide (pressed powder, density 797 kg/m3) | MgO | 47,6 | 0,607 |
| Copper(II) oxide (pressed powder) | CuO | 45,6 | 1,013 |
| Sodium chloride | NaCl | 0 | 1,116 |
| Naphthalene | S10N8 | 0 | 0,377 |
| 1-Naphthol | С10Н8О | 35 | 0,293 |
| 2-Naphthol | С10Н8О | 35 | 0,335 |
| Nickel(III) oxide (pressed powder, density 1445 kg/m3) | Ni2O3 | 46,2 | 0,938 |
| Sulfur: | S | ||
| rhombic | 0 | 0,293 | |
| plastic | 20–100 | 0,264 | |
| Silver bromide | AgBr | 0 | 1,03 |
| Silver chloride | AgCl | 0 | 1,089 |
Table 3.7.4
Thermal conductivity coefficients of thermal insulation, building and some other materials
| Material | T, °С | λ, W/(m K) |
| Asbestos fabric | 20 | 0,279 |
| Asbestos fiber | 0 | 0,112 |
| 100 | 0,121 | |
| Asbestos cardboard | 100 | 0,144 |
| Asphalt | 20 | 0,744 |
| Basalt | 20 | 2,175 |
| Concrete | 20 | 0,922 |
| Bauxite | 600 | 0,557 |
| Woolen felt | 40 | 0,073 |
| Gypsum | 0 | 1,297 |
| Fireproof clay | 300–600 | 0,875–0,925 |
| Granite | 20 | 3,419 |
| Tree: | ||
| birch (10.8% humidity), + fibers | 29 | 0,172 |
| oak (density 825 kg/m3), + fibers | 15 | 0,209 |
| oak (density 819 kg/m3), ¦ fibers | 20 | 0,349 |
| Diatomaceous earth | 20 | 0,055 |
| Charcoal | 81 | 0,076 |
| Limestone | 0 | 2,07 |
| Clay lime | 20 | 3,256 |
| Coal | 20 | 0,186 |
| Corrugated cardboard | 0,064 | |
| Brick: | ||
| insulating | 100 | 0,14 |
| refractory | 200 | 1,006 |
| building | 20 | 0,233–0,291 |
| Clinker | 30 | 0,163 |
| Powdered coke | 100 | 0,191 |
| Ice | 0 | 2,25 |
| –95 | 3,954 | |
| Magnesite | 1000 | 1,663 |
| Marble: | ||
| white | 3,268 | |
| black | 30 | 2,861 |
| Boiler room scale | 65 | 1,31–3,14 |
| Onyx | 30 | 2,34 |
| Wood sawdust | 20 | 0,07 |
| Paraffin | 20 | 0,267 |
| Sand: | ||
| dry | 20 | 0,326 |
| wet | 20 | 1,13 |
| Sandstone (density 2259 kg/m3) | 40 | 1,84 |
| Portland cement | 30 | 0,302 |
| Cork granulated | 20 | 0,038 |
| Cork plate | 30 | 0,042 |
| Soft rubber | 20 | 0,167 |
| Slate | 100 | 1,49 |
| Mica | 0,582 | |
| Snow: | ||
| freshly fallen | 0,105 | |
| compacted | 0,048 | |
| Glass wool | 0 | 0,037 |
| Textolite | 20 | 0,645–0,93 |
| Peat slabs | 50 | 0,064 |
| Porcelain | 95 | 1,04 |
| Fiber (plates) | 20 | 0,049 |
| Fluorite | 0 | 10,4 |
| Mineral wool | 50 | 0,047 |
| Cinder concrete | 0,93 | |
| Slag wool | 100 | 0,07 |
| Plaster | 20 | 0,779 |
| Cotton (density 81 kg/m3) | 0 | 0,057 |
| Ebonite | 0 | 0,158 |
| Material | T, °С | λ, W/(m K) |
Table 3.7.5
Thermal conductivity coefficients λ (W/(m K)) of some liquid metal coolants
| Coolant | Temperature, °C | ||||||||||
| 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 | 700 | |
| Bismuth (Tm = 271.3 °C; Tbp = 1560 °C) | 14,7 | 15,6 | 16,5 | 17,3 | 18,3 | ||||||
| Potassium (Tm = 63.6 °C; Tbp = 776 °C) | 46,5 | 46,4 | 45,9 | 44,9 | 43,4 | 39,5 | 34,9 | 30,9 | 28,3 | ||
| Lithium (Tm = 180 °C; Tbp = 1350 °C) | 46,1 | 46,3 | 46,6 | 47,1 | 47,6 | 48 | 48,5 | ||||
| Sodium (Tm = 97.8 °C; Tbp = 900 °C) | 86,1 | 84,1 | 81,6 | 78,7 | 75,5 | 68,7 | 63,8 | 60,6 | 59,1 | ||
| Tin (Tm = 231.9 °C; Tbp = 2720 °C) | 30,7 | 31,6 | 33,6 | 35,5 | 37,4 | 39,4 | |||||
| Mercury (Tm = –38.9 °C; Tbp = 356.6 °C) | 7,79 | 8,43 | 9,07 | 9,71 | 10,4 | 11 | 11,6 | 12,6 | 13,3 | ||
| Lead (Tm = 327.3 °C; Tbp = 1751 °C) | 15,1 | 15,5 | 15,9 | 17,7 | |||||||
| Sodium-potassium alloy: 25% Na + 75% K (Tm = 11 °C; Tbp = 784 °C) | 22,7 | 23,3 | 23,8 | 24,5 | 25,1 | 25,8 | 27,1 | 28,4 | 29,7 | 30,9 | |
| Lead-bismuth alloy: 44% Pb + 55.5% Bi (Tm = 123.5 °C; Tbp = 1670 °C) | 11,2 | 11,7 | 12,2 | 12,7 | 13,7 | 14,7 | 15,8 | 16,7 | |||
Table 3.7.6
Thermal conductivity coefficients of pure organic liquids
| Name | Formula | T, °С | λ, W/(m K) |
| Aniline | С6H7N | 16,5 | 0,1774 |
| Acetaldehyde | С2H4O | 21 | 0,1712 |
| Acetone | С3Н6О | 16 | 0,1902 |
| Benzene | C6H6 | 16 | 0,1902 |
| Bromobenzene | С6Н5Br | 20 | 0,1115 |
| 2-Bromobutane | C4H9Br | 12 | 0,1164 |
| 1-Bromopentane | С5H11Br | 18 | 0,0984 |
| 1-Bromopropane | С3Н7Br | 12 | 0,1076 |
| Bromoethane | С2Н5Br | 30 | 0,1198 |
| Butan-1-ol | С4H10O | 20 | 0,1534 |
| Butyl acetate | С6Н12О2 | 20 | 0,1369 |
| Hexane | S6H14 | 30–100 | 0,1376 |
| Hexan-1-ol | С6H14O | 30–100 | 0,1615 |
| Heptane | S7N16 | 30 | 0,1404 |
| Heptan-1-ol | С7H16O | 70–100 | 0,1625 |
| Glycerol | С3Н8О3 | 20 | 0,2943 |
| Dean | S10N22 | 30 | 0,1402 |
| Diisopropyl ether | С6Н14О | 20 | 0,1097 |
| Difluorodichloromethane (Freon-12) | СCl2F2 | 20 | 0,08248 |
| Difluorochloromethane (Freon-22) | CHClF2 | 20 | 0,09295 |
| Dichloromethane (methylene chloride) | CH2Cl2 | 0 | 0,1218 |
| 1,2-Dichloropropane | С3Н6Cl2 | 20–50 | 0,1254 |
| 1,2-Dichloroethane (ethylene chloride) | С2Н4Cl2 | 20 | 0,1264 |
| Diethyl ether | С4Н10О | 30 | 0,1375 |
| N,N-Diethylethanamine (triethylamine) | С6Н15N | 20 | 0,121 |
| Isobutyric acid | С4Н8О2 | 12 | 0,1424 |
| Isopropyl acetate | С5Н10О2 | 20 | 0,1344 |
| 1-Isopropyl-4-methylbenzene (n-cymene) | S10N14 | 30 | 0,1347 |
| 2-Isopropyl-5-methylphenol (thymol) | С10H14O | 13 | 0,1311 |
| Iodobenzene | С6Н5I | 30–100 | 0,1203 |
| 2-Iodobutane | С4Н9I | 12 | 0,08709 |
| 1-Iodopentane | С5H11I | 12 | 0,08499 |
| 1-Iodopropane | С3Н7I | 12 | 0,09211 |
| Iodoethane | С2Н5I | 30 | 0,111 |
| m-Cresol | С7Н8О | 20 | 0,1499 |
| n-Cresol | С7Н8О | 20 | 0,1444 |
| o-Xylene | С8Н10 | –20÷80 | 0,1428 |
| m-Xylene | С8Н10 | 25 | 0,1577 |
| Butyric acid | С4Н8О2 | 12 | 0,1507 |
| Mesitylene | S11N12 | 20 | 0,1359 |
| Methanol | CH4O | 20 | 0,2023 |
| Methyl acetate | С3Н6О2 | 12 | 0,1612 |
| 3-Methylbutan-1-ol | С5H12O | 0 | 0,1478 |
| (3-Methylbutyl)acetate | С7Н14О2 | 20 | 0,1298 |
| 2-Methylpropan-1-ol | С4H10O | 20 | 0,1424 |
| 1-Methyl-3-chlorobenzene | С7Н7Сl | 20 | 0,1298 |
| Methylcyclohexane | S7N14 | 30 | 0,1278 |
| Formic acid | CH2O2 | 12 | 0,2713 |
| Nitrobenzene | С6Н5NO2 | 30–100 | 0,1636 |
| Nitromethane | CH3NO2 | 30 | 0,2153 |
| Nonan | С9Н20 | 30–100 | 0,1413 |
| Nonan-1-ol | С9H20O | 30–100 | 0,1681 |
| Octane | S8N18 | 30 | 0,1452 |
| Octan-1-ol | С8H18O | 30–100 | 0,1663 |
| Oleic acid | С18Н34О2 | 26,5 | 0,2309 |
| Palmitic acid | С16Н32О2 | 72,5 | 0,1715 |
| Pentane | С5H12 | 30 | 0,1349 |
| Pentan-1-ol | С5H12O | 30–100 | 0,1622 |
| Pentachloroethane | С2НCl5 | 20 | 0,1254 |
| Pentyl acetate | С7Н14О2 | 20 | 0,1292 |
| Propane-1,2-diol | С3Н8О2 | 20–80 | 0,2009 |
| Propan-1-ol | С3H8O | 12 | 0,1562 |
| Propan-2-ol | С3H8O | 20 | 0,1408 |
| Prop-2-en-1-ol | С3Н6O | 30 | 0,1798 |
| Propyl acetate | С5Н10О2 | 12 | 0,1369 |
| Propyl formate | С4Н8О2 | 12 | 0,1537 |
| Propionic acid | С3Н6О2 | 12 | 0,1633 |
| Stearic acid | С18Н36О2 | 72,5 | 0,1601 |
| 1,1,2,2-Tetrafluoro-1,2-dichloroethane (Freon-114) | С2Cl2F4 | 30 | 0,0775 |
| Carbon tetrachloride | СCl4 | 20 | 0,1034 |
| 1,1,2,2-Tetrachloroethane | С2H2Cl4 | 20 | 0,1139 |
| Tetrachlorethylene | CCl2=CCl2 | 20 | 0,1619 |
| Toluene | S7N8 | 20 | 0,1349 |
| 1,1,2-Trifluoro-1,2,2-trichloroethane (Freon-113) | С2Cl3F3 | 30 | 0,09085 |
| Trichlorethylene | CHCl=CCl2 | 20 | 0,1162 |
| Acetic acid | С2Н4О2 | 20 | 0,172 |
| Acetic anhydride | С4H6O3 | 21 | 0,2213 |
| Fluorodichloromethane (Freon-21) | CHCl2F | 0,108 | |
| Fluorotrichloromethane (Freon-11) | CCl3F | 20 | 0,09546 |
| Chlorobenzene | C6H5Cl | 30–100 | 0,1447 |
| 2-Chlorobutane | C4H9Cl | 12 | 0,1164 |
| Chloromethane | CH3Cl | –15÷30 | 0,1925 |
| Chloroform | CHCl3 | 20 | 0,103 |
| 1-Chloropentane | С5H11Cl | 12 | 0,1185 |
| 1-Chloropropane | С3Н7Cl | 12 | 0,1185 |
| Ethanol | С2H6O | 20 | 0,1673 |
| Ethyl acetate | С4Н8О2 | 16 | 0,1491 |
| Ethylbenzene | С8Н10 | 20 | 0,1323 |
| Ethylene glycol | С2Н6О2 | 20 | 0,2611 |
| Name | Formula | T, °С | λ, W/(m K) |
Table 3.7.7
Thermal conductivity coefficients λ (W/(m K)) of some refrigerants in the liquid state
| Refrigerant | Formula | Temperature, °C | ||||||
| –30 | –20 | –10 | 0 | 10 | 20 | 30 | ||
| Ammonia | NH3 | 0,57 | 0,57 | 0,558 | 0,547 | 0,518 | ||
| Difluorodichloromethane (Freon-12) | СCl2F2 | 0,106 | 0,101 | 0,097 | 0,092 | 0,087 | 0,083 | 0,078 |
| Sulfur dioxide | SO2 | 0,223 | 0,207 | 0,212 | 0,205 | 0,199 | 0,193 | |
| Carbon dioxide | CO2 | 0,151 | 0,14 | 0,128 | 0,116 | 0,093 | 0,07 | |
| Fluorotrichloromethane (Freon-11) | CCl3F | 0,12 | 0,115 | 0,11 | 0,106 | 0,101 | 0,095 | 0,091 |
| Chloromethane | CH3Cl | 0,188 | 0,179 | 0,171 | 0,162 | 0,154 | ||
Odds
Heat transfer table of steel pipes
| Connection type | For pipes with internal diameter, mm | Δt, °С | |||
| 50 — 60 | 60 — 70 | 70 — 80 | 80 — 100 | ||
| In one thread | up to 40 | 11,5 | 12 | 12,5 | 12,5 |
| 50-100 | 10 | 10,5 | 11 | 11,5 | |
| over 125 | 10 | 10,5 | 10,5 | 10,5 | |
| In several threads | up to 40 | 10 | 11 | 11,5 | 11,5 |
| over 50 | 8 | 9 | 9 | 9 | |
The figures given are for pipes with wall thicknesses of 3 mm and above.
A heated towel rail for a stainless steel bathroom, although it belongs to the smooth pipes considered, will have to be calculated using a different coefficient due to the difference between black and stainless steel. With a thermal pressure Δt = 70-80 °C for pipes of different diameters, the following values are taken:
| Du, mm | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| k | 15 | 14,5 | 13,3 | 12 | 11 | 10 | 9 | 8 |
It should be borne in mind that the dryer for towels in the bathroom, if it is not an old part of the heating system, is usually made of two sizes of pipes. Therefore, for the coil and connecting jumpers of smaller diameter, the coefficient k is selected separately.
Whatever system you have to calculate, a floor-standing water heated towel rail or heating registers, you will need one more coefficient. It will allow you to bring the result obtained in units of Kcal/h to the usual form W/h. To do this, Q is multiplied by 1.163.
SNiP 2.04.01-85 requires that a steel heated towel rail have a heat output of at least 100 W per unit area of the room (1 m2) and at least 40 W per 1 m3 of bathroom. Therefore, after converting the heat transfer into the appropriate units of measurement, you can determine for what size rooms the selected drying design is suitable.
Thermal conductivity of steel and cast iron
The table shows the thermal conductivity values of steel and cast iron.
The thermal conductivities of steels are given for the following types: carbon, low- and medium-alloyed, heat-resistant and heat-resistant stainless steels, spring steels, steels for castings, tool steels, depending on temperature.
The thermal conductivity of steel in the table is presented for various grades in the temperature range from -263 to 1200°C.
The average thermal conductivity of carbon steels (type steel 08, steel 3, steel 20) at room temperature is 50...90 W/(m deg). The thermal conductivity of stainless, heat-resistant and heat-resistant martensitic steels lies in the range from 30 to 45 W/(m deg). The thermal conductivity of stainless steels (type 12Х18Н9Т) of the austenitic class is in the range from 12 to 22 W/(m deg).
How many watts will a copper heating pipe with an outer diameter of 22 mm and a length of 1 meter produce?
IMHODom › Forums › communications and heating › How many watts will a copper heating pipe with an outer diameter of 22 mm and a length of 1 meter produce?
- This topic has 4 voices and 9 replies.
How to calculate (or where to find out) how many watts a copper heating pipe with an outer diameter of 22 mm and a length of 1 meter will produce (single, running horizontally, unobstructed from the air)? For example, for the conditions - the air around the pipe is at a temperature of 20 degrees, the coolant (and the pipe, accordingly, too) is 70 degrees.
Stupidity is not a lack of intelligence, it is such intelligence. (A.I.Lebed)
I have a steel pipe along a 40mm wall, 38 meters long. This results in an area of 4.77 m2 of painted steel. Very impressive heat dissipation!
d - additional heat losses associated with cooling of the coolant in the supply and return lines passing in unheated rooms, kW. Q value
d is recommended to be determined with an efficiency coefficient, insulation of 0.75, according to table. 2.
temperature of the coolant at the entrance to the heating system (for supply pipelines) or at the exit from it (for return pipelines), °C; tв
— air temperature of the rooms in which the pipelines are laid, °C; defining
... (0.022x pi) x 1m = 0.07 m2 is very small.
I have a steel pipe along a 40mm wall, 38 meters long. This results in an area of 4.77 m2 of painted steel. Very impressive heat dissipation!
Very little for what? I ask how much “in grams,” and you say “not enough,” “impressive.” Can you be more precise, at least give an approximate figure? I will be grateful.
Well, thank you. Sorry for being vague in this area, but (I) need clarification. Did I understand the table correctly: if the coolant temperature is 60 degrees, and the room is 20 degrees, then for a 20 mm pipe and 75% thermal insulation efficiency, 20 watts per linear meter will be consumed in the water? Please explain the term “thermal insulation coefficient”. If it is 0.75, then 25% of the heat goes into the air, or vice versa - 75? Accordingly, a clarifying question: if there is no thermal insulation at all, then each meter of such a pipe will produce 27 watts?
Stupidity is not a lack of intelligence, it is such intelligence. (A.I.Lebed)
Here is a link with all the calculations and formulas:
And the insulation coefficient is 0.75, as I understand it, this is a coefficient that takes into account the ineffectiveness of heat removal from the pipe, associated with its position, which prevents normal convection, paint on the pipe, etc. Those. with a pipe located in the center of the room, without difficulty in air convection around it, without additional coating, this coefficient. =1. (tabular values must be multiplied by 1.25).
Pipes made from alternative materials
To figure out when which pipes can be used for heating, you need to compare them according to several parameters and answer a number of questions:
- What kind of heating system will there be - forced or gravity.
- Type of pipe installation - inside or outside the wall, simple or complex system configuration.
- Maximum and operating pressure and temperature in the system.
- Price
After analyzing this data, you can choose your option.
Iron pipes
Today, the market offers a large selection of iron pipes, although their use has been reduced to use in a gravity autonomous heating system using large-sized pipes. The main advantage of these pipes remains their strength; they cannot be damaged mechanically. They are resistant to high temperatures (over 1500˚C) and pressure. Moisture has little effect on metal, since with prolonged circulation of the same coolant in the system, oxygen quickly evaporates from it. The practice of operating iron pipes shows that their service life is more than 20 years.
The disadvantage is the complexity of installation; a qualified welder is needed to connect the pipes, which leads to a significant increase in the cost of the structure, and repairs in an already lived-in room will lead to damage to the wallpaper and furniture if it cannot be moved. Iron pipes are susceptible to corrosion, so it is not advisable to install them inside the wall. Also, iron pipes do not have a very attractive appearance and require painting every year. But high thermal conductivity indoors is an advantage; it increases heat transfer, whereas when passing through unheated areas, it can significantly lose heat and requires insulation. The price of such pipes is not high.
Ways to increase heat transfer
In all heating and heating systems, it is necessary to strive to ensure that the heat transfer of the pipe is maximum. This will mean that we use the energy spent on heating the carrier most efficiently. For each design operating under its own conditions, a method to increase heat transfer is selected separately, taking into account all the nuances. But the basis for these improvements will be the initial data already considered in the theoretical calculation - the area of the radiating surface and the temperature difference.
Calculation of the heat transfer coefficient of a flat wall
You can calculate the heat transfer coefficient of a flat surface using the similarity equation:
Nul = 0.66×Rel 0.5×Pr 0.33; with a laminar boundary layer
Nul = 0.037×Rel 0.8×Pr 0.43; with a turbulent boundary layer
Rel is the Reynolds number, Pr is the Prandtl number.
Initial data:
L is the surface size in the direction of flow, millimeters;
w—flow velocity, meters per second;
μ—dynamic viscosity of the coolant, in pascal×second;
ρ—coolant density, in kilograms/meter 3;
Heat loss through pipes
In apartment conditions, there is no particular point in calculating the heat transfer of a stainless pipe, because in this case all the heat given off by the riser and heating circuits will be dissipated inside, heating the room.
But if it is necessary to efficiently heat basement or warehouse facilities, and the coolant must be supplied to them from another place, then in this case, calculating the heat transfer of the pipe will be more than advisable so that you can figure out how much heat is lost along the way. Then you can try to look for ways to reduce heat loss from hot water pipes.
Importance in everyday life and production
Why is it important to consider thermal conductivity? A similar value is indicated in various tables for each metal and is taken into account in the following cases:
- In the manufacture of various heat exchangers. Heat is one of the important carriers of energy. It is used to provide comfortable living conditions in residential and other premises. When creating heating radiators and boilers, it is important to ensure rapid and complete heat transfer from the coolant to the end consumer.
- In the manufacture of outlet elements. You can often encounter a situation where you need to remove heat rather than supply it. An example is the case of heat removal from the cutting edge of a tool or gear teeth. To ensure that the metal does not lose its basic performance qualities, rapid removal of thermal energy is ensured.
- When creating insulating layers. In some cases, the material should not conduct thermal energy transfer. For such operating conditions, a metal is selected that has a low heat conductivity coefficient.
Registers
The simplest design of heating radiators is registers. These are medium- or large-diameter pipes welded at the ends, single or connected in sections by jumper tubes. They can be seen in entrances, at industrial facilities or in private houses with individual heating.
Steel pipelines are considered traditional for the construction of water supply, sewerage and underground gas supply systems. To increase their thermal power, a method of increasing the area is used - thin metal plates are welded. This improves the heat transfer of the battery by almost one and a half times. Compact radiators, the closest relatives of cast iron accordion batteries, have approximately the same heat transfer. Although they are, of course, far from panel bimetallic devices.
To ensure maximum heat transfer from heating radiators, a simple and inexpensive convection method is used. This method involves hanging the device correctly. It is installed as close to the floor as possible, where cold air accumulates, but the gaps necessary for circulation are left, including near the wall itself.
Installation subtleties
Sometimes the flexibility of corrugated pipes for heating or water supply turns from an advantage into a disadvantage, which must be remembered in the following situations:
- In difficult places in the system, do not repeatedly bend the corrugated part. During operation, this place will be a weak link, since bending loads will exceed permissible values.
Heat exchangers for heating a private house (in a brick oven) Source ytimg.com
- If there are children in the house, it is worth considering how to secure the system. Children's imagination can easily turn a flexible part into a convenient support or crossbar. Sooner or later, fatigue will accumulate in the material with all the ensuing (in every sense) consequences.
Installation of corrugated stainless steel pipes for heating includes the following operations:
- A piece of the required size is cut from the bay, for which a grinder or pipe cutter is used. If necessary, the cut site is cleared of burrs.
- The pipes are connected using fittings. In this case, you must ensure that the diameters match and the union nut is tightly tightened.
- If necessary, the pipeline is fixed to the wall using brackets.
- Lastly, water is supplied to make sure the joint is tight.
A pipe cutter allows you to obtain a cut without deforming the pipe Source rothenberger-russia.ru
Application of thermal insulation materials
Probably the first thing that comes to mind when it is necessary to retain maximum heat inside a pipe is to wrap it with heat-insulating material. At the end of the last century, fiberglass insulation with additional winding with non-flammable fabric was used for these purposes (this method is recommended by the regulatory framework). A little earlier, solutions of gypsum or cement were actively used, that is, the thermal insulation was solid. In reality, careless plumbers often simply wrapped the pipes with old rags, hoping that no one would check.
The abundance of modern materials, such as foam pipe linings, split polyethylene shells, mineral wool and others, allows for much better thermal insulation of heating pipes. And in new buildings such materials are successfully used. However, the backwardness of housing and communal services often leads to the fact that pipes are wrapped in rags the old fashioned way.
Thermal conductivity of steel at different temperatures
So what is thermal conductivity? From a physics point of view, thermal conductivity
– this is the molecular transfer of heat between directly contacting bodies or particles of the same body with different temperatures, in which the energy of movement of structural particles (molecules, atoms, free electrons) is exchanged.
To put it simply, thermal conductivity
is the ability of a material to conduct heat. If there is a temperature difference inside the body, then thermal energy moves from the hotter part of the body to the colder part.
Heat transfer occurs due to the transfer of energy when molecules of a substance collide. This happens until the temperature inside the body becomes the same.
This process can occur in solid, liquid and gaseous substances.
In practice, for example in construction for the thermal insulation of buildings, another aspect of thermal conductivity is considered, associated with the transfer of thermal energy. Let's take an “abstract house” as an example.
In the “abstract house” there is a heater that maintains a constant temperature inside the house, say, 25 ° C. The temperature outside is also constant, for example, 0 °C.
It is quite clear that if you turn off the heater, then after a while the house will also be 0 °C. All the heat (thermal energy) will go through the walls to the street.
To maintain the temperature in the house at 25 ° C, the heater must be constantly running. The heater constantly creates heat, which constantly escapes through the walls to the street.
Coefficient of thermal conductivity
The amount of heat that passes through the walls (and according to science, the intensity of heat transfer due to thermal conductivity) depends on the temperature difference (in the house and outside), on the area of the walls and the thermal conductivity of the material from which these walls are made.
To quantify thermal conductivity, there is a coefficient of thermal conductivity of materials . This coefficient reflects the property of a substance to conduct thermal energy. The higher the thermal conductivity coefficient of a material, the better it conducts heat.
If we are going to insulate a house, then we need to choose materials with a small value of this coefficient. The smaller it is, the better. Nowadays, the most widely used materials for insulating buildings are mineral wool insulation and various foam plastics.
A new material with improved thermal insulation properties – Neopor – is gaining popularity.
The thermal conductivity coefficient of materials is designated by the letter ? (Greek small letter lambda) and is expressed in W/(m2*K). This means that if you take a brick wall with a thermal conductivity coefficient of 0.67 W/(m2*K), a thickness of 1 meter and an area of 1 m2.
, then with a temperature difference of 1 degree, 0.67 watts of thermal energy will pass through the wall. If the temperature difference is 10 degrees, then 6.7 watts will pass. And if, with such a temperature difference, the wall is made 10 cm, then the heat loss will already be 67 watts.
More details about the methodology for calculating heat loss in buildings can be found here.
It should be noted that the values of the thermal conductivity coefficient of materials are indicated for a material thickness of 1 meter. To determine the thermal conductivity of a material for any other thickness, the thermal conductivity coefficient must be divided by the desired thickness, expressed in meters.
In building codes and calculations the concept of “thermal resistance of a material” is often used. This is the reciprocal of thermal conductivity. If, for example, the thermal conductivity of foam plastic 10 cm thick is 0.37 W/(m2*K), then its thermal resistance will be equal to 1 / 0.37 W/(m2*K) = 2.7 (m2*K)/ Tue
Thermal conductivity coefficient of materials
The table below shows the values of the thermal conductivity coefficient for some materials used in construction.
| Material | Coeff. warm W/(m2*K) |
| Alabaster slabs | 0,470 |
| Aluminum | 230,0 |
| Asbestos (slate) | 0,350 |
| Fibrous asbestos | 0,150 |
| Asbestos cement | 1,760 |
| Asbestos cement slabs | 0,350 |
| Asphalt | 0,720 |
| Asphalt in floors | 0,800 |
| Bakelite | 0,230 |
| Concrete on crushed stone | 1,300 |
| Concrete on sand | 0,700 |
| Porous concrete | 1,400 |
| Solid concrete | 1,750 |
| Thermal insulating concrete | 0,180 |
| Bitumen | 0,470 |
| Paper | 0,140 |
| Light mineral wool | 0,045 |
| Heavy mineral wool | 0,055 |
| Cotton wool | 0,055 |
| Vermiculite sheets | 0,100 |
| Woolen felt | 0,045 |
| Construction gypsum | 0,350 |
| Alumina | 2,330 |
| Gravel (filler) | 0,930 |
| Granite, basalt | 3,500 |
| Soil 10% water | 1,750 |
| Soil 20% water | 2,100 |
| Sandy soil | 1,160 |
| The soil is dry | 0,400 |
| Compacted soil | 1,050 |
| Tar | 0,300 |
| Wood - boards | 0,150 |
| Wood – plywood | 0,150 |
| Hardwood | 0,200 |
| Chipboard | 0,200 |
| Duralumin | 160,0 |
| Reinforced concrete | 1,700 |
| Wood ash | 0,150 |
| Limestone | 1,700 |
| Lime-sand mortar | 0,870 |
| Iporka (foamed resin) | 0,038 |
| Stone | 1,400 |
| Multilayer construction cardboard | 0,130 |
| Foamed rubber | 0,030 |
| Natural rubber | 0,042 |
| Fluorinated rubber | 0,055 |
| Expanded clay concrete | 0,200 |
| Silica brick | 0,150 |
| Hollow brick | 0,440 |
| Silicate brick | 0,810 |
| Solid brick | 0,670 |
| Slag brick | 0,580 |
| Siliceous slabs | 0,070 |
| Brass | 110,0 |
| Ice 0°C | 2,210 |
| Ice -20°С | 2,440 |
| Linden, birch, maple, oak (15% humidity) | 0,150 |
| Copper | 380,0 |
| Mipora | 0,085 |
| Sawdust - backfill | 0,095 |
| Dry sawdust | 0,065 |
| PVC | 0,190 |
| Foam concrete | 0,300 |
| Polystyrene foam PS-1 | 0,037 |
| Polyfoam PS-4 | 0,040 |
| Polystyrene foam PVC-1 | 0,050 |
| Foam resopen FRP | 0,045 |
| Expanded polystyrene PS-B | 0,040 |
| Expanded polystyrene PS-BS | 0,040 |
| Polyurethane foam sheets | 0,035 |
| Polyurethane foam panels | 0,025 |
| Lightweight foam glass | 0,060 |
| Heavy foam glass | 0,080 |
| Glassine | 0,170 |
| Perlite | 0,050 |
| Perlite-cement slabs | 0,080 |
| Sand 0% moisture | 0,330 |
| Sand 10% moisture | 0,970 |
| Sand 20% humidity | 1,330 |
| Burnt sandstone | 1,500 |
| Facing tiles | 1,050 |
| Thermal insulation tile PMTB-2 | 0,036 |
| Polystyrene | 0,082 |
| Foam rubber | 0,040 |
| Portland cement mortar | 0,470 |
| Cork board | 0,043 |
| Cork sheets are lightweight | 0,035 |
| Cork sheets are heavy | 0,050 |
| Rubber | 0,150 |
| Ruberoid | 0,170 |
| Slate | 2,100 |
| Snow | 1,500 |
| Scots pine, spruce, fir (450…550 kg/cub.m, 15% humidity) | 0,150 |
| Resinous pine (600…750 kg/cub.m, 15% humidity) | 0,230 |
| Steel | 52,0 |
| Glass | 1,150 |
| Glass wool | 0,050 |
| Fiberglass | 0,036 |
| Fiberglass | 0,300 |
| Wood shavings - stuffing | 0,120 |
| Teflon | 0,250 |
| Paper roofing felt | 0,230 |
| Cement boards | 1,920 |
| Cement-sand mortar | 1,200 |
| Cast iron | 56,0 |
| Granulated slag | 0,150 |
| Boiler slag | 0,290 |
| Cinder concrete | 0,600 |
| Dry plaster | 0,210 |
| Cement plaster | 0,900 |
| Ebonite | 0,160 |
Heated towel rails
The bathroom heated towel rail itself is a clear example of how the heat transfer of a pipe can be improved. The “coil” of the device is nothing more than an artificially increased area of thermal radiation. Since previously they were only part of the general heating line, it was not possible to change the diameter of the steel pipe. Therefore, the heat transfer area was increased by simply increasing the length.
By the way, a stainless steel water heated towel rail would look good in black. Shiny and chrome-plated products, although they look beautiful, interfere with heat exchange between the pipe and the environment.
For vertically oriented systems, such as radiators and heated towel rails, the method of connecting the inlet and outlet pipes matters. The heat transfer of one device with different installations can change significantly:
- 100% efficiency – diagonal connection (hot water inlet at the top, outlet at the back at the bottom);
- 97% – one-sided with top entrance;
- 88% – lower two-way connection;
- 80% – reverse diagonal (with bottom entry);
- 78% – one-sided with bottom inlet and outlet of waste water.
Polyethylene is the simplest waterproofing for underfloor heating, it also increases heat transfer
Minuses
The disadvantages include the following features:
- Stainless steel is not a cheap raw material, and a corrugated stainless pipe for heating from the best manufacturers costs a decent amount.
- If you plan to design a heated floor, experts recommend using corrugation in a polyethylene braid that protects against contact with chemically active substances. In addition, the concrete screed should be replaced with a “dry” installation method.
- Corrugated pipes have an “industrial” look that will not fit into every design. On sale you can find corrugated polymer shells in different colors, which leaves some room for maneuver.
- The recesses between the corrugation rings sooner or later fill with dust, which is not so easy to clean out.
Warm floor
Not so long ago, a warm floor from a heated towel rail or room radiator became a continuation of the overall heating system in the apartment, significantly increasing the area of the heating surface. But water as a coolant in this situation can create many problems.
No matter how reliable steel pipes are, they do not last forever, and joints, especially threaded ones, can leak over time. Just imagine that this happened inside a concrete screed that cannot be easily removed. For this reason, water-based heated floors are practically not used.
If you do decide to implement this system, you will have to think about how to make it as efficient as possible. The power of a heated floor must be calculated with extreme accuracy. But if the numbers show that heat transfer is insufficient, you need to first take care of increasing the efficiency of steel pipes.
Since this design does not come into contact with the air in the room, but heats the floor materials, you can only play by increasing the length of the pipes. That’s why they are laid in a compact but long “snake”. Thanks to its large surface area, it transfers a lot of heat.
A caveat: when several linear meters of pipe are tightly laid, the heat transfer of the heated floor as a whole will increase, and for each individual segment, not critically, but will decrease.
The reason is that pipes located too close partially exchange heat with each other. A heated zone is created around each, which leads to a slight decrease in thermal pressure.
Application and labeling
Stainless steel corrugation is used in the following cases:
- When installing heating systems of private houses, bathhouses, greenhouses (usually a product with a diameter of 20 mm is used). They help connect heating appliances to the heating riser.
- When installing standard water supply pipelines and connecting plumbing fixtures.
- When installing heated floors and varieties (warm walls, baseboards); in heating radiators.
- As cable ducts for protecting electrical cables.
- In fire extinguishing systems as a fire-fighting pipeline.
- When laying communication networks.
- In gas supply systems.
- In internal combustion engines: transports fuel and removes exhaust gases.
Product markings indicate how they can be used:
- With the letter "A". The corrugation is made of unannealed steel.
- With the letter "M". Annealing technology was used.
Connecting a corrugated pipe to a fitting Source prodomostroy.ru
- With the letter "P". The pipe is protected by an additional plastic sheath.
- With the letter combination “El”. For electricians.
See also: Catalog of companies that specialize in engineering systems (heating, water supply, sewerage and others) and related work
Products – Tekhmashholding – group of companies, official website
- Choosing pots and pans can be quite a daunting task. The shape of the cookware and handle, the materials used, the design and purpose are all factors that influence the choice. Understanding the differences in the materials used to make cookware is the first step to gaining clarity on how cookware works and what is important when choosing one.
Basic principles
The purpose of the cookware is to transfer energy from its source to the product. There are two main sources: gas and electricity. In both cases, the heat is not transferred evenly: the gas is distributed into individual small tongues of flame, and the electricity, as a rule, flows in a spiral, leaving places where the heat does not flow. Since heat is supplied unevenly, the cook's job is to compensate for this through cooking techniques or using utensils. High-quality cookware must not only be durable, but also efficient in the process of transferring energy from source to product. There are several factors that influence this ability. The two main ones are thermal conductivity and heat capacity. All discussions about cookware materials focus on these factors.
Thermal conductivity
Thermal conductivity is the ability of a material to absorb and transmit energy. When the heating element comes into contact with the pan, heat is transferred to the pan. This increases the internal kinetic energy of the pan (heating occurs). A heated object transfers energy to neighboring materials that have a lower temperature. The higher the thermal conductivity, the faster a given object heats up and the faster the heated parts of a given object transfer heat to parts that have not yet been touched. For example, if we place a large sheet of stainless steel (which has a rather low thermal conductivity, if we talk about materials for cookware) on the heating element, then the picture will be like this: the part that is located next to the heating element will heat up, while the remaining areas will warm up rather slowly. When the heat reaches remote areas of the sheet, its central part, located on the heat source, will simply be red-hot. One solution to the problem is to make the sheet thicker. The lower part of the sheet will not heat up equally with the upper part, since it is located at a smaller distance from the heating element. Thus, energy must be transferred from the lower layers to the upper ones so that the upper part is heated more evenly. In the picture we see a cut of the steel sheet and the heating zone. The central heating point (white) cooled over time, so the heat was transferred to the higher layers of steel. As a result, we see more uniform heating, however, it is not ideal. The thicker the steel, the more uniform the heating of the surface. Unfortunately, low thermal conductivity means that the overall heating process slows down, and the response of the material (pan) to an increase or decrease in temperature also slows down. For most cooking processes, it is desirable for cookware to heat up quickly, have an even temperature, and respond to changes in temperature. Materials with high thermal conductivity meet these demands, as they quickly transfer heat, rapidly distribute it over the entire surface of the material and quickly respond to temperature changes. Here is a table of materials and their level of thermal conductivity:
| Material | Thermal conductivity |
| Copper | 401 W/m*K |
| Aluminum | 237 W/m*K |
| Cast iron | 80 W/m*K |
| Carbon steel | 51 W/m*K |
| Stainless steel | 16 W/m*K |
Heat capacity
The amount of kinetic energy stored in a material is called heat capacity. This is not the same as temperature, which is the average molecular kinetic energy within a material. So, for example, 1 kg of water at a temperature of 100 degrees contains more energy than 1 kg of steel at the same temperature. While thermal conductivity is responsible for the ability of a material to absorb energy, heat capacity is the amount of energy that can heat or cool a material. Heat capacity is proportional to the mass of the material, so 2 kg of metal has a heat capacity twice as high as 1 kg of metal. This means that those dishes that have a high heat capacity heat up slowly, but will keep warm for a long time. When energy is released, the material cools, but at a much slower rate compared to materials with low heat capacity. Cast iron is one that is often referred to as a material with high heat capacity. The heat capacity of 1 kg of cast iron is several times less than that of aluminum, but due to its large weight, the overall heat capacity is higher. The thickness of the material in the cookware is often indicated by the manufacturer (for example, 3 mm aluminum), but since the heat capacity directly depends on the weight of the product, you also need to know the density of the material.
| Material | Heat capacity per 1 kg | density |
| Aluminum | 910 J/kg*K | 2600 kg/m3 |
| Stainless steel | 500 J/kg*K | 7500 – 8000 kg/m3 |
| Carbon. Steel | 500 J/kg*K | 7500 – 8000 kg/m3 |
| Cast iron | 460 J/kg*K | 7900 kg/m3 |
| Copper | 390 J/kg*K | 8900 kg/m3 |
By multiplying the heat capacity by the density of the material, you will find that the heat capacity of a stainless steel, cast iron or copper unit is one and a half times higher than that of aluminum. Thus, you would need an aluminum pan one and a half times thicker to get the same heat capacity.
Thermal diffusion
You may have noticed that I slightly misled you when I explained about thermal conductivity. The fact is that thermal conductivity does not independently determine how quickly the pan will heat up and how quickly the heat will spread to all its parts. By and large, heat capacity also matters in this matter. It would be great to have only one unit of measurement for this parameter, wouldn't it? And there is such a unit - this is thermal diffusion. So, let's look at the table.
| Material | Thermal diffusion |
| Copper | 120 * 10-6 m2/s |
| Aluminum | 100 * 10-6 m2/s |
| Cast iron | 22 * 10-6 m2/s |
| Carbon. steel | 14 * 10-6 m2/s |
| Stainless steel steel | 4.3 * 10-6 m2/s |
According to this table, the best parameters are copper and aluminum. And now we come to the final concept - reactivity.
Reactivity
Not only should we be interested in the thermal properties of materials, but we also need to make sure that the materials we use in our cookware are not harmful to us and do not negatively affect the taste of our food. It turns out that we also need a non-reactive material. Unfortunately, copper and aluminum quickly come into chemical contact with food. The entry of copper particles into the body can lead to diseases of the liver, stomach, and kidneys. Every cookbook mentions that an yolk beaten occasionally in a copper bowl can't harm you, but on the other hand, you cook every day... And aluminum can even cause Alzheimer's disease. Therefore, in addition to high thermal diffusivity, we also wanted would be a non-reactive material. On the other hand, stainless steel, the least reactive of all the popular materials used in cookware, also has the worst thermal diffusivity. It turns out that physics is not our friend today. But the magic of cookware companies lies in solutions for the production of cookware with high thermal diffusion and at the same time non-reactive. There are several options for solving this problem: combining copper with a non-reactive surface (tinned copper), steel utensils with a copper and aluminum disk, aluminum and steel alloys. The table below shows the effectiveness of these solutions from the most successful to the least productive.
| Rank | Compound |
Heat transfer at the molecular level
When matter heats up, the average kinetic energy of its constituent particles increases, that is, the level of disorder increases, atoms and molecules begin to oscillate more intensely and with greater amplitude around their equilibrium positions in the material.
Heat transfer, which at the macroscopic level can be described by Fourier's law, at the molecular level is the exchange of kinetic energy between particles (atoms and molecules) of a substance, without transfer of the latter. This explanation of the mechanism of thermal conduction at the molecular level distinguishes it from the mechanism of thermal convection, in which heat transfer occurs due to the transfer of matter. All solids have the ability to conduct heat, while thermal convection is possible only in liquids and gases. Indeed, solids transfer heat mainly due to thermal conductivity, and liquids and gases, if there are temperature gradients in them, transfer heat mainly due to convection processes.