Young's modulus (synonyms: modulus of elasticity of the first kind, modulus of longitudinal elasticity) is a mechanical characteristic of materials that determines their ability to resist longitudinal deformations. Shows the degree of hardness of the material.
Named after the English scientist Thomas Young.
Denoted by the Latin capital letter E
The unit of measurement is Pascal [Pa].
In the strength of materials, the modulus of longitudinal elasticity is involved in calculations of rigidity in tension-compression and bending, as well as in calculations of stability.
Given that almost all structural materials have a high-order E value (usually 10 9 Pa), its dimension is often written using the multiple prefix “giga” (gigapascal [GPa])
For all materials, its value can be determined during an experiment to determine the elastic modulus of the first kind.
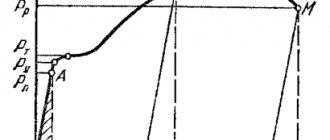
The approximate value of the modulus can be determined from the stress diagram obtained during tensile tests.
Rice. 1 Initial fragment of the voltage diagram
In this case, Young's modulus is equal to the ratio of normal stresses to the corresponding relative deformations, in the section of the diagram (Fig. 1) up to the limit of proportionality σ pc
(tangent of the angle α of the inclination of the section of proportionality to the axis of deformation ε).
Table 1 provides comparative modulus values for some of the most commonly used materials
Elastic properties of bodies
Below are reference tables for commonly used constants; if two of them are known, then this is quite sufficient to determine the elastic properties of a homogeneous isotropic solid.
Young's modulus or modulus of longitudinal elasticity in dynes/cm2.
Shear modulus or torsional modulus G in dynes/cm2.
Compressive modulus or bulk modulus of elasticity K in dynes/cm2.
Compressibility volume k=1/K/.
Poisson's ratio µ is equal to the ratio of transverse relative compression to longitudinal relative tension.
For a homogeneous isotropic solid material, the following relationships between these constants hold:
K = E / 3(1 – 2μ) – (c)
Poisson's ratio has a positive sign and its value is usually between 0.25 and 0.5, but in some cases it can go beyond these limits. The degree of agreement between the observed values of µ and those calculated using formula (b) is an indicator of the isotropy of the material.
Tables of Young's Modulus of Elasticity, Shear Modulus and Poisson's Ratio
Values calculated from relations (a), (b), (c) are given in italics.
Material at 18°C
Young's modulus E, 10 11 dynes/cm2.
Shear modulus G, 10 11 dynes/cm2.
Poisson's ratio µ
Modulus of bulk elasticity K, 10 11 dynes/cm 2.
When calculating concrete and reinforced concrete structures for the second group of limit states, in particular when determining deflections, it is necessary to know the elastic modulus E (Young's modulus) of concrete under compression. In this case, it is necessary to distinguish between the initial Eb and the reduced Eb1 elastic moduli.
Table of material elasticity indicators
Before moving directly to this characteristic of steel, let us first consider, as an example and additional information, a table containing data on this value in relation to other materials. Data is measured in MPa.
Modulus of elasticity of various materials
As you can see from the table above, this value is different for different materials, and the indicators also differ, if we take into account one or another option for calculating this indicator. Everyone is free to choose exactly the option for studying indicators that suits them best. It may be preferable to consider Young's modulus, since it is most often used specifically to characterize a particular material in this regard.
After we have briefly reviewed the data on this characteristic of other materials, we will move directly to the characteristics of steel separately.
First, let's look at the hard numbers and derive different indicators of this characteristic for different types of steels and steel structures:
- Modulus of elasticity (E) for casting, hot-rolled reinforcement from steel grades called St.3 and St. 5 equals 2.1*106 kg/cm^2.
- For steels such as 25G2S and 30KhG2S this value is 2*106 kg/cm^2.
- For periodic wire and cold-drawn round wire, there is an elasticity value equal to 1.8 * 106 kg/cm^2. For cold-flattened reinforcement the indicators are similar.
- For strands and bundles of high-strength wire the value is 2·10 6 kg/cm^2
- For steel spiral ropes and ropes with a metal core, the value is 1.5·10 4 kg/cm^2, while for cables with an organic core this value does not exceed 1.3·10 6 kg/cm^2.
- The shear modulus (G) for rolled steel is 8.4·10 6 kg/cm^2.
- And finally, Poisson’s ratio for steel is equal to 0.3
These are general data given for types of steel and steel products. Each value was calculated in accordance with all physical rules and taking into account all existing relationships that are used to derive the values of this characteristic.
Below will be given all the general information about this characteristic of steel. Values will be given both by Young's modulus and by shear modulus, both in one unit of measurement (MPa) and in another (kg/cm2, newton*m2).
Steel and several different grades
| Material | Elastic modulus indicators (E, G; N*m2, kg/cm^2, MPa) |
| Steel | 20.6*10^10 newton*meter^2 |
| Carbon steel | E=(2.0…2.1)*10^5 MPa; G=(8.0…8.1)*10^4 MPa |
| Steel 45 | E=2.0*10^5 MPa; G=0.8*10^5 MPa |
| Steel 3 | E=2.1*10^5 MPa; G=0.8*10^5 MPa |
| Alloy steel | E=(2.1…2.2)*10^5 MPa; G=(8.0…8.1)*10^4 MPa |
The elasticity values of steel vary, since there are several modules at once, which are calculated and calculated in different ways. You can notice the fact that, in principle, the indicators do not differ greatly, which indicates in favor of different studies of the elasticity of various materials. But it’s not worth going too deep into all the calculations, formulas and values, since it’s enough to choose a certain elasticity value in order to focus on it in the future.
By the way, if you do not express all the values in numerical ratios, but take it immediately and calculate it completely, then this characteristic of steel will be equal to: E = 200,000 MPa or E = 2,039,000 kg/cm^2.
This information will help you understand the very concept of modulus of elasticity, as well as become familiar with the main values of this characteristic for steel, steel products, and also for several other materials.
It should be remembered that the elastic modulus indicators are different for different steel alloys and for different steel structures that contain other compounds. But even in such conditions, you can notice the fact that the indicators do not differ much. The elastic modulus of steel practically depends on the structure. and also on carbon content. The method of hot or cold processing of steel also cannot greatly affect this indicator.
Elastic deformations. Young's modulus and Poisson's ratio. Energy of elastic deformation.
Determination of the initial modulus of elasticity of concrete B20, B25
All bodies are deformable
.
Changes caused by the actions of applied forces, during which bodies change shape and volume - deformations
.
Elastic
deformations
are deformations that disappear after the applied force ceases.
Plastic deformations
(
residual deformations
) – deformations that remain in the body (partially or completely) after the cessation of the applied force.
If the voltage
(force per unit area) does not exceed a certain value (
elastic limit
), then the deformation will be elastic.
Perfectly elastic
bodies – bodies that can only undergo elastic deformations.
For such bodies there is an unambiguous relationship between the forces and the deformations they cause
.
Small deformations
– deformations that obey
Hooke’s law
, according to which
deformations are proportional to the forces causing them isotropic anisotropic
Let there be two rods. We squeeze one, and squeeze the other with force (as in the picture). Let us draw a section perpendicular to the axis of the rod. To balance the rod, a force must act on its lower base. The lower and upper parts of the rod act on each other with equal force, because they are deformed. Ratio of force to cross-sectional area - stress
.
Tension
– tensile stress, .
Pressure
– compressive stress, where is the cross-sectional area. Pressure is negative voltage and vice versa.
– length of the undeformed rod. – length increment after application of force. That means full length. – relative elongation of the rod (if – relative compression).
For small elastic deformations, tension (pressure) is proportional to relative elongation (relative compression) -
(),
where is Young’s modulus
(constant, depending only on the material of the rod and its physical state).
Young's modulus
- the tension that must be applied to the rod so that its length doubles.
And the two formulas above are Hooke’s law
.
Let's calculate the elastic energy
stretched rod. Let us apply a tensile force to the rod and gradually (continuously and slowly) increase it from to . The elongation will vary from to . According to Hooke's law,
where is the elasticity coefficient
.
All work on stretching the rod will go towards increasing its elastic energy. Because in the final state, then , then for energy we get .
Under the action of a tensile or compressive force, not only the longitudinal but also the transverse dimensions of the rod change. If the force is tensile, then the transverse dimensions of the rod decrease. If it is compressive, then they increase.
– Poisson's ratio
.
It depends only on the material of the body in question. Young's modulus and Poisson's ratio fully characterize the elastic properties of an isotropic material. All other elastic deformations can be expressed through these coefficients.
Post Views: 4,220
iSopromat.ru
Poisson's ratio (transverse deformation coefficient) is one of the mechanical characteristics of materials, shows the relationship between longitudinal and transverse deformations of an element, and characterizes the elastic properties of the material.
It is denoted by the lowercase Greek letters ν or μ and has no dimension.
Determined by the ratio of relative transverse ε pop
and longitudinal ε
pr
deformations of the beam (element):
The procedure for determining the transverse deformation coefficient:
Let us consider the deformation of a cylindrical element (Fig. 1) which before loading has the following dimensions:
Rice. 1. Dimensions of timber before loading
here h
— initial longitudinal size;
d
is the initial transverse dimension (in this case, diameter).
After loading with some longitudinal system of forces (for example, compressive), the beam will change its dimensions, the longitudinal dimension will decrease (due to compression) and the transverse dimension, on the contrary, will increase (Fig. 2).
Rice. 2. Dimensions of the timber after deformation
The dimensions obtained as a result of deformation will be denoted by h1
and
d1
, where:
here Δh
and Δ
d
are the absolute longitudinal and transverse deformations, respectively.
The ratio of absolute deformations to the corresponding initial dimensions will show the relative deformations:
and their ratio in turn determines the Poisson’s ratio of the timber material.
The value of the coefficient is taken modulo, because longitudinal and transverse deformations always have opposite signs (elongation of the beam leads to its narrowing and vice versa).
Table 1 shows comparative coefficient values for some materials.
Source
Modulus of elasticity of various materials
Gsm module for boiler
Elastic moduli for different materials have completely different values, which depend on:
- the nature of the substances that form the composition of the material;
- mono- or multicomponent composition (pure substance, alloy, etc.);
- structures (metallic or other type of crystal lattice, molecular structure, etc.);
- density of the material (distribution of particles in its volume);
- the processing to which it was subjected (firing, etching, pressing, etc.).
Its significance for bronze materials depends not only on the processing, but also on the chemical composition:
- bronze – 10.4 GPa;
- aluminum bronze during casting – 10.3 GPa;
- rolled phosphor bronze – 11.3 GPa.
Young's modulus of brass is much lower - 78.5-98.1. Rolled brass has the maximum value.
Copper itself in its pure form is characterized by a resistance to external influences that is much greater than its alloys - 128.7 GPa. Processing it also reduces the indicator, including rolling:
- cast – 82 GPa;
- rolled – 108 GPa;
- deformed – 112 GPa;
- cold drawn – 127 GPa.
Titanium (108 GPa), which is considered one of the strongest metals, has a value close to copper. But heavy but brittle lead shows only 15.7-16.2 GPa, which is comparable to the strength of wood.
For iron, the stress-to-strain ratio also depends on the method of its processing: cast - 100-130 or forged - 196.2-215.8 GPa.
Cast iron is known for its brittleness and has a stress-to-strain ratio of 73.6 to 150 GPa, which is consistent with its type. Whereas for steel, the elastic modulus can reach 235 GPa.
Elastic moduli of some materials
The values of strength parameters are also influenced by the shape of the products. For example, for a steel rope, calculations are carried out, which take into account:
- its diameter;
- lay pitch;
- lay angle.
Interestingly, this figure for a rope will be significantly lower than for a wire of the same diameter.
It is worth noting the strength and non-metallic materials. For example, among the Young's moduli of wood, pine has the lowest - 8.8 GPa, but the group of hardwoods, which are united under the name "iron wood", has the highest - 32.5 GPa, oak and beech have equal indicators - 16.3 GPa.
Among building materials, the resistance to external forces of seemingly durable granite is only 35-50 GPa, while even glass is 78 GPa. Concrete is inferior to glass - up to 40 GPa, limestone and marble, with values of 35 and 50 GPa, respectively.
Flexible materials such as rubber can withstand axial loads ranging from 0.0015 to 0.0079 GPa.
Steel 45 structural carbon quality
Substitutes
Foreign analogues
| Germany (DIN) | C45, C45E+QT, Ck45, Cm45 |
| Euronorms (EN) | 1.0503, 1.1191 |
| USA | M1044, 1044, 1045, M1045 |
| Japan | S45C, S48C |
IMPORTANT. The possibility of replacement is determined in each specific case after assessing and comparing the properties of steels
Decoding
The number 45 indicates the average carbon content in hundredths of a percent, i.e. The carbon content in steel 45 is 0.45%.
Characteristics and purpose
Steel grade 45 refers to structural carbon unalloyed special quality steels with normal manganese content.
Steel grade 45 is used for the manufacture of:
- sucker rod couplings,
- gear shaft,
- centrifugal pump shafts,
- mud pump rods,
- fingers of crossheads of mud pumps,
- compressors,
- rotors,
- barrels and swivel subs,
- subs for working and drill pipes,
- core bit bodies,
- preventer rollers,
- bevel gears,
- gears,
- clamps and keys of drilling rigs,
- sprocket wheels of drilling drawworks,
- pins,
- thrust screws,
- rolling pin pumps,
- trunnions,
- crankshafts and camshafts,
- spindles,
- bandages,
- cylinders,
- fists,
- other normalized, improved and surface heat treated parts that require increased strength.
The use of steel 45 for parts of valves and pneumatic actuators that do not work under pressure and are not subject to welding, intended for operation at low temperatures
| steel grade | Quenching + tempering at temperature, °C | Approximate strength level, N/mm2 (kgf/mm2) | Application temperature not lower than, °C | Use in thickness no more than, mm |
| 45 | 500 | 900 (90) | -50 | 20 |
- When heat treated for strength below that specified in column 3 or when used in parts with a wall thickness of less than 10 mm, the operating temperature may be reduced.
- The maximum thickness indicated in column 5 is due to the need to obtain through hardenability and uniformity of properties across the cross section.
Use of steel 45 for the manufacture of fasteners (GOST 32569-2013)
| steel grade | Technical requirements | Acceptable operating parameters | Purpose | |
| Wall temperature, °C | Medium pressure, MPa (kgf/cm2), no more | |||
| Steel 45 GOST 1050 GOST 10702 | STP 26.260.2043 | -40 to +425 | 10(100) | Studs, bolts |
| 16(160) | Nuts | |||
| -40 to +450 | Washers | |||
Limits of application, types of mandatory testing and control of steel 45 for flanges for pressures above 10 MPa (100 kgf/cm2) (GOST 32569-2013)
| steel grade | Technical requirements | the name of detail | Limit parameters | Mandatory tests | Control | |||||||
| Wall temperature, °C no more | Nominal pressure, MPa (kgf/cm2), no more | σ0.2, MPa | σв, MPa | δ5, % | ψ% | KCU, J/cm2 | Hardness HB | Flaw detection | Non-metallic inclusions | |||
| Steel 45 GOST 1050 GOST 10702 | GOST 9399 | Flanges | -40 to +200 | 32(320) | 16(160) | + | + | + | + | + | + | — |
Resistance of steel 45 against crevice erosion
NOTE. The coefficient of erosion resistance of a material is the ratio of the rate of erosive wear of the material to the rate of erosive wear of steel 12Х18Н10Т (taken as 1).
The use of steel 45 for the manufacture of main parts of AC fittings
| Material | Type of semi-finished product or product | Maximum permissible temperature of use, °C | |
| Name | Brand, ND for material | ||
| Carbon steel | Steel 45 GOST 1050 | Forgings, long products. Fasteners | 350 |
Type of delivery
- long products, including shaped steel: GOST 1050-88, GOST 2590-88, GOST 2591-88, GOST 2879-88, GOST 8509-93, GOST 8510-86, GOST 8239-89, GOST 8240-89, GOST 10702 -78.
- Calibrated rod GOST 1050-74, GOST 7417-75, GOST 8559-75, GOST 8560-78, GOST 10702-78.
- Polished rod and silver steel GOST 14955-77, GOST 10702-78.
- Thick sheet GOST 1577-93, GOST 19903-74.
- Thin sheet GOST 16523-89.
- Tape GOST 2284-79.
- Strip GOST 1577-93, GOST 103-76, GOST 82-70.
- Wire GOST 17305-91, GOST 5663-79.
- Forgings and forged blanks GOST 8479-70, GOST 1133-71.
- Pipes GOST 8732-78, GOST 8733-74, GOST 8734-75, GOST 8731-74, GOST 21729-76.
Chemical composition, % (GOST 1050-88)
Chemical composition, % (GOST 1050-2013)
| Steel grade | steel grade | Mass fraction of elements, % | |||||||
| C | Si | Mn | P | S | Cr | Ni | Cu | ||
| no more | |||||||||
| Unalloyed special | 45 | 0,42-0,50 | 0,17-0,37 | 0,50-0,80 | 0,030 | 0,035 | 0,25 | 0,30 | 0,30 |
Heat treatment
Parts made of steel grade 45 are subjected to normalization at a temperature of 860-880 ° C or quenching in water from a temperature of 840-860 ° C followed by tempering; The tempering temperature is set depending on the required mechanical properties (Fig. below).
For example, parts of drilling rigs (gears, retainer, keys), preventer (main support plate, rollers) are tempered at a temperature of 550°C, and sprockets of a drill drawworks are tempered at a temperature of 500°C.
Effect of nitriding on the endurance limit of steel 45
For parts subject to wear at low contact loads, carbon steel grade 45 is strengthened using short-term nitriding conditions (520-570 °C, Holding 1-6 hours). At the same time, despite a slight increase in hardness, an increase in antifriction properties, resistance to alternating loads and corrosion is ensured.
| steel grade | Sample type | Endurance limit, kgf/mm2 | |
| after improvement | after nitriding | ||
| 45 | Smooth, d = 7.5 mm | 44 | 61 |
- Nitriding was carried out at 520-540°C, layer depth 0.35-0.45 mm.
- On samples with a diameter of 7.5 mm, a notch is made with an angle of 60° and a depth of 0.3 mm.
Hardness of the hardened layer after tempering HRCе during high-frequency hardening
Temperature of critical points, °C
Hardness HB (Brinell) for metal products made of steel 45 (GOST 1050-2013)
| steel grade | no more | |||
| hot rolled and forged | calibrated and with special surface finishing | |||
| without heat treatment | after annealing or high tempering | hard-worked | after annealing or high tempering | |
| 45 | 229 | 197 | 241 | 207 |
Hardness on hardened samples HRC (Rockwell) (GOST 1050-2013)
Mechanical properties of rolled products
| GOST | Delivery status | Section, mm | σв, MPa | δ5(δ4), % | ψ% |
| no less | |||||
| GOST 1050-88 | Hot-rolled, forged, calibrated and silver steel of the 2nd category after normalization | 25 | 600 | 16 | 40 |
| Calibrated steel of the 5th category after hardening | Samples | 640 | 6 | 30 | |
| GOST 10702-78 | Steel, calibrated and calibrated with a special finish after tempering or annealing | — | Up to 590 | — | 40 |
| GOST 1577-93 | Standardized and hot-rolled sheet | 80 | 590 | 18 | — |
| Normalized or hot rolled strip | 6-25 | 600 | 16 | 40 | |
| GOST 16523-89 | Hot rolled sheet (transverse samples) | Up to 2 2-3.9 | 550-690 | (14) (15) | — |
| Cold rolled sheet | Up to 2 2-3.9 | 550-690 | (15) (16) | — | |
Mechanical properties of forgings (GOST 8479-70)
| Heat treatment | Section, mma | σ0.2, MPa | σв, MPa | δ5, % | ψ% | KCU, J/cm2 | Hardness HB , no more |
| no less | |||||||
| Normalization | 100-300 | 245 | 470 | 19 | 42 | 39 | 143-179 |
| 300-500 | 17 | 35 | 34 | ||||
| 500-800 | 15 | 30 | 34 | ||||
| Up to 100 | 275 | 530 | 20 | 40 | 44 | 156-197 | |
| 100-300 | 17 | 38 | 34 | ||||
| Hardening, tempering | 300-500 | 15 | 32 | 29 | |||
| Normalization, hardening + tempering | Up to 100 | 315 | 570 | 17 | 38 | 39 | 167-207 |
| 100-300 | 14 | 35 | 34 | ||||
| 300-500 | 12 | 30 | 29 | ||||
| Up to 100 | 345 | 590 | 18 | 45 | 59 | 174-217 | |
| 100-300 | 345 | 590 | 17 | 40 | 54 | 174-217 | |
| Up to 100 | 395 | 620 | 17 | 45 | 59 | 187-229 | |
Mechanical properties depending on tempering temperature
| tot, °С | σ0.2, MPa | σв, MPa | δ5, % | ψ% | KCU, J/cm2 | Hardness HB , no more |
| Quenching at 850 °C in water. Samples with a diameter of 15 mm | ||||||
| 450 | 830 | 980 | 10 | 40 | 59 | — |
| 500 | 730 | 830 | 12 | 45 | 78 | — |
| 550 | 640 | 780 | 16 | 50 | 98 | — |
| 600 | 590 | 730 | 25 | 55 | 118 | — |
| Quenching at 840 °C in water. Workpiece diameter 60 mm | ||||||
| 400 | 520-590 | 730-840 | 12-14 | 46-50 | 50-70 | 202-234 |
| 500 | 470-520 | 680-770 | 14-16 | 52-58 | 60-90 | 185-210 |
| 600 | 410-440 | 610-680 | 18-20 | 61-64 | 90-120 | 168-190 |
Mechanical properties at elevated temperatures
| tsp, °С | σ0.2, MPa | σв, MPa | δ5, % | ψ% | KCU, J/cm2 |
| Normalization | |||||
| 200 | 340 | 690 | 10 | 36 | 64 |
| 300 | 255 | 710 | 22 | 44 | 66 |
| 400 | 225 | 560 | 21 | 65 | 55 |
| 500 | 175 | 370 | 23 | 67 | 39 |
| 600 | 78 | 215 | 33 | 90 | 59 |
| Specimen with a diameter of 6 mm and a length of 30 mm, forged and normalized. Deformation speed 16 mm/min; strain rate 0.009 1/s | |||||
| 700 | 140 | 170 | 43 | 96 | — |
| 800 | 64 | 110 | 58 | 98 | — |
| 900 | 54 | 76 | 62 | 100 | — |
| 1000 | 34 | 50 | 72 | 100 | — |
| 1100 | 22 | 34 | 81 | 100 | — |
| 1200 | 15 | 27 | 90 | 100 | — |
Mechanical properties depending on the section
| Section, mm | σ0.2, MPa | σв, MPa | δ5, % | ψ% | KCU, J/cm2 |
| no less | |||||
| 15 | 640 | 780 | 16 | 50 | 98 |
| 30 | 540 | 730 | 15 | 45 | 78 |
| 75 | 440 | 690 | 14 | 40 | 59 |
| 100 | 440 | 690 | 13 | 40 | 49 |
NOTE. Quenching at 850°C, tempering at 550°C. Samples were cut from the center of the blanks.
Endurance limit
| Strength characteristics | σ-1, MPa | τ-1, MPa |
| σ0.2 = 310 MPa, σв = 590 MPa | 245 | 157 |
| σ0.2 = 680 MPa, σв = 880 MPa | 421 | — |
| σ0.2 = 270 MPa, σв = 520 MPa | 231 | — |
| σ0.2 = 480 MPa, σв = 660 MPa | 331 | — |
Impact strength KCU
| Heat treatment | KCU, J/cm2, at temperature, °C | |||
| +20 | -20 | -40 | -60 | |
| Rod with a diameter of 25 mm | ||||
| Hot rolling | 14-15 | 10-14 | 5-14 | 3-8 |
| Annealing | 42-47 | 27-34 | 27-31 | 13 |
| Normalization | 49-52 | 37-42 | 33-37 | 29 |
| Hardening + tempering | 110-123 | 72-88 | 36-95 | 31-63 |
| Rod with a diameter of 120 mm | ||||
| Hot rolling | 42-47 | 24-26 | 15-33 | 12 |
| Annealing | 47-52 | 32 | 17-33 | 9 |
| Normalization | 76-80 | 45-55 | 49-56 | 47 |
| Hardening + tempering | 112-164 | 81 | 80 | 70 |
Technological properties
Forging temperature, °C: beginning 1250, end 750. Sections up to 400 mm are cooled in air.
Cutting machinability - Kv tv.spl = 1 and Kv b.st = 1 in the hot-rolled state at HB 170-179 and σw = 640 MPa.
Tendency to temper brittleness - not prone.
Weldability
Steel 45 is difficult to weld. Welding methods: RDS and KTS. Heating and subsequent heat treatment are required.
Hardenability, mm (GOST 1050-88)
The hardenability band of steel 45 after normalization at 850 °C and quenching from 830 °C is shown in the figure below.
Critical diameter d
Physical and mechanical properties of steel 45 (Nuclear energy PNAE G-7-002-86)
| Assortment | Characteristic | Temperature, K (°C) | ||||||||||||
| 293 (20) | 323 (50) | 373 (100) | 423 (150) | 473 (200) | 523 (250) | 573 (300) | 623 (350) | |||||||
| Hot-rolled section steel with a thickness or diameter of up to 250 mm | RTm, MPa (kgf/cm2) | 598 (61) | 598 (61) | 598 (61) | 598 (61) | 598 (61) | 579 (59) | 559 (57) | 540 (55) | |||||
| RTp0.2, MPa (kgf/cm2) | 353 (36) | 343 (35) | 343 (35) | 343 (35) | 343 (35) | 294 (30) | 255 (26) | 235 (24) | ||||||
| A,% | 16 | 13 | 10 | 9 | 7 | 10 | 15 | 15 | ||||||
| Z,% | 40 | 37 | 33 | 30 | 30 | 30 | 30 | 30 | ||||||
| Blanks of fasteners with a thickness or diameter of 300 mm, KP315* | RTm, MPa (kgf/cm2) | 569 (58) | 569 (58) | 569 (58) | 569 (58) | 569 (58) | 549 (56) | 530 (54) | 510 (52) | |||||
| RTp0.2, MPa (kgf/cm2) | 315 (32) | 304 (31) | 304 (31) | 294 (30) | 274 (28) | 255 (26) | 245 (25) | 225 (23) | ||||||
| A,% | 14 | 12 | 12 | 12 | 12 | 12 | 12 | 17 | ||||||
| Z,% | 35 | 33 | 33 | 33 | 33 | 33 | 35 | 35 | ||||||
| The same, from 100 to 800 mm, KP245* | RTm, MPa (kgf/mm2) | 470(48) | 470 (48) | 470 (48) | 470 (48) | 470 (48) | 461 (47) | 441 (45) | 412 (42) | |||||
| RTp0.2, MPa (kgf/mm2) | 245 (25) | 235 (24) | 235 (24) | 235 (24) | 235 (24) | 206 (21) | 177 (18) | 167 (17) | ||||||
| A, % | 14 | 12 | 10 | 8 | 6 | 8 | 13 | 13 | ||||||
| Z, % | 30 | 27 | 23 | 23 | 23 | 23 | 23 | 23 | ||||||
| The same, up to 800 mm, KP275* | RTm, MPa (kgf/mm2) | 530(54) | 530(54) | 530(54) | 530(54) | 530(54) | 510(52) | 491(50) | 481(49) | |||||
| RTp0.2, MPa (kgf/mm2) | 275(28) | 265(27) | 265(27) | 265(27) | 265(27) | 226(23) | 196(20) | 196(20) | ||||||
| A, % | 12 | 10 | 8 | 6 | 5 | 8 | 11 | 11 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
| The same, up to 800 mm, KP315* | RTm, MPa (kgf/mm2) | 570 (58) | 570 (58) | 570 (58) | 570 (58) | 570 (58) | 549 (56) | 530 (54) | 510 (52) | |||||
| RTp0.2, MPa (kgf/mm2) | 315 (32) | 304 (31) | 304 (31) | 304 (31) | 304 (31) | 255 (26) | 226 (23) | 206 (21) | ||||||
| A, % | 10 | 8 | 6 | 5 | 4 | 7 | 10 | 10 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
| Forgings with a diameter of up to 300 mm, KP345* | RTm, MPa (kgf/mm2) | 590(60) | 590(60) | 590(60) | 590(60) | 590(60) | 569(58) | 549(56) | 530(54) | |||||
| RTp0.2, MPa (kgf/mm2) | 345(35) | 333(34) | 333(34) | 333(34) | 333(34) | 284(29) | 245(25) | 226(23) | ||||||
| A, % | 10 | 8 | 6 | 5 | 4 | 7 | 10 | 10 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
| The same, up to 100 mm, KP395* | RTm, MPa (kgf/mm2) | 615(63) | 615(63) | 615(63) | 615(63) | 615(63) | 598(61) | 579(59) | 559(57) | |||||
| RTp0.2, MPa (kgf/mm2) | 395(40) | 395(40) | 395(40) | 395(40) | 395(40) | 333(34) | 294(30) | 275(28) | ||||||
| A, % | 10 | 8 | 6 | 5 | 4 | 7 | 10 | 10 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
- Both significant figures are included in the "from" and "to" limits
- RTm - minimum value of tensile strength at design temperature, MPa (kgf/mm2)
- RTp0.2 - minimum value of the yield strength at the design temperature, MPa (kgf/mm2)
Physical properties
Density ρ kg/cm3
| Steel grade | At test temperature, °C | |||||||||
| 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 45 | 7826 | 7799 | 7769 | 7735 | 7698 | 7662 | 7625 | 7587 | 7595 | — |
Modulus of normal elasticity E, GPa
| Steel grade | At test temperature, °C | |||||||||
| 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 45 | 200 | 201 | 193 | 190 | 172 | — | — | — | — | — |
Modulus of elasticity in torsional shear G, GPa
Linear expansion coefficient α*106, K-1
| steel grade | α*106, K-1 at test temperature, °C | |||||||||
| 20-100 | 20-200 | 20-300 | 20-400 | 20-500 | 20-600 | 20-700 | 20-800 | 20-900 | 20-1000 | |
| 45 | 11,9 | 12,7 | 13,4 | 14,1 | 14,6 | 14,9 | 15,2 | — | — | — |
Thermal conductivity coefficient λ W/(m*K)
| Steel grade | λ W/(m*K), at test temperature, °C | |||||||||
| 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 45 | — | 48 | 47 | 44 | 41 | 39 | 36 | 31 | 27 | 26 |
Factors affecting Young's modulus
Prices for stainless steel fencing per meter
Young's modulus is the main characteristic of concrete that determines its strength. Due to its size, designers carry out calculations of the material’s resistance to various types of loads. The indicator is influenced by many factors:
- quality and quantity of aggregates;
- concrete class;
- air humidity and temperature;
- time of exposure to load factors;
- reinforcement.
PHOTO: dostroy.comThe modulus of elasticity allows designers to correctly calculate the load
Quality and quantity of aggregates
The quality of concrete depends on its aggregates. If the components have low density, accordingly, Young's modulus will be small. The elasticity of the material increases several times if heavy fillers are used.
PHOTO: russkaya-banja.ruLarge components increase elasticity characteristics
PHOTO: ivdon.ru Graph of the dependence of the tensile strength of a material on cement stone
Material class
The class of concrete also influences the coefficient: the lower it is, the lower the value of the elastic modulus. For example:
- the elastic modulus of B10 corresponds to a value of 19;
- B15 – 24;
- V-20 – 27.5;
- B25 – 30;
- the indicator for B30 increases to a value of 32.5.
PHOTO: buildingclub.ruDependence on concrete class
How do humidity and temperature values affect the indicator?
The increase in deformations and decrease in the elastic properties of the material are influenced by:
- increase in air temperature;
- increase in solar activity.
Under the influence of negative environmental factors, the internal energy of the material increases, this leads to linear expansion of concrete and, accordingly, to an increase in plasticity.
The creep of the material is affected by moisture, leading to a change in elastic characteristics. The higher the water vapor content, the lower the coefficient.
PHOTO: betonpro100.ru The influence of humidity on the creep of concrete
Load exposure time and mixture hardening conditions
The elasticity index is affected by the time of exposure to the load:
- with an instantaneous force on a concrete structure, the deformability is directly proportional to the magnitude of the external load;
- with prolonged exposure, the coefficient values decrease.
During the research, it was noted that if concrete hardens naturally, its elastic modulus is higher, in contrast to steaming the material under various conditions. This is explained by the fact that when external conditions are used, large quantities of voids and pores are formed in concrete, worsening its elastic properties.
PHOTO: udarnik.spb.ru Dependence of elastic moduli on various factors
Age of concrete and reinforcement of the structure
The strength of concrete is directly dependent on its age; over time, the indicator only increases. Another factor that has a positive effect on the elastic modulus of concrete is reinforcement, which prevents deformation of the material.
PHOTO: 63-ds.netsamara.ru For structures that will be operated under heavy loads, it is necessary to install a metal grid
Modulus of elasticity of wood
Wood is considered elastic if, after removing the force that bends it, it returns to its original shape. Elasticity has a limit. It is achieved when, when bent, a wooden part or product retains its final shape. Simply put, the elastic limit of the board is reached at the moment when it breaks. The properties of elasticity and flexibility are not identical. Flexibility is the ability to change shape under the influence of external influences. Elasticity – the ability to regain lost shape. Wood with a high modulus is necessary for making sports equipment and furniture. The most elastic wood is from species such as ash, beech, hazel, and larch.
To describe the ability to return to its original shape, the following physical quantities are used:
- modulus of elasticity E;
- deformation coefficient µ;
- shear modulus G.
In general, we can say that when a force is applied along wood fibers, the modulus of elasticity is 20-25 times higher than if the same force acts across the fibers. If the force acts perpendicular to the direction of the fibers and is directed radially, then this figure is 20-50% greater than when the same force is applied in the tangential direction.
Below we will consider in more detail these physical quantities that determine the ability of wood to return to its original shape when the deforming force is removed.
Modulus of elasticity of basic wood species
The modulus of elasticity in physics is considered as a single name for a complex of physical quantities that characterize the ability of a solid body (in our case, wood) to elastically deform if some force is applied to it.
The modulus of elasticity of wood (E) is the relationship between normal stresses and relative deformations. It is measured in MPa or kgf/cm2 (1 MPa=10.197 kgf/cm2) There are several types:
- along the fibers of Ea.
- across the grain (tangential) Et.
- across the fibers (radial) Er.
- modulus of elasticity in bending Ebg.
Table. Information on the most commonly used breeds.*
Transverse deformation coefficients of main wood species
When a load is applied, in addition to longitudinal deformation along the fibers, transverse deformation also appears during bending.
The coefficients of this type of deformation are given in the table:
Shear modulus of basic wood species
Shear modulus is the proportionality coefficient between shear stresses and angular deformations of wood.
Shear modulus data for the main rocks is given below:
Plasticity of wood
A tree is capable of changing its shape under pressure without destruction, and retaining it after the pressure is removed. This property is called plasticity. Plasticity depends on the same criteria as elasticity, only in the opposite direction. For example, the higher the moisture content of wood, the more plastic it is, but less elastic.
The plasticity of wood is increased with the help of special processing. By steaming or boiling it in water, we obtain a more plastic material, which is then used to make furniture and sleigh runners. The highest plasticity is found in beech, elm, ash, and oak. This property is due to the structure of the conductive system of these rocks. Beech, for example, has many large medullary rays that bend the wood fibers. The vessels located in groups in the annual layers of elm, oak, and ash are strongly compressed by denser late wood, so the plasticity of these species is high.
Mechanical properties of structural and stainless steels
Steels used in mechanical engineering are divided into structural (carbon and alloy) and high-alloy stainless . The grade of structural carbon steel contains a two-digit number indicating the average carbon content in hundredths of a percent. In the designation of grades of structural alloy steel ( GOST 4543 ), the first two digits indicate the average carbon content in hundredths of a percent, and the letters behind the numbers indicate: P - boron, Yu - aluminum, C - silicon, T - titanium, F - vanadium, X - chromium, G - manganese, N - nickel, M - molybdenum, V - tungsten. The numbers after the letter indicate the approximate percentage of the alloying element in whole percentage units; the absence of numbers means that the steel contains up to 1.5% of this alloying element. The letter A is placed at the end of the name of the high-quality steel grade. For especially high-quality steel, the letter Ш is placed at the end of the brand designation, separated by three dashes. In grades of stainless high-alloy steels (GOST 5632), the chemical elements are designated by the following letters: A - nitrogen, B - tungsten, D - copper, M - molybdenum, P - boron, T - titanium, Yu - aluminum, X - chromium, B - niobium, G - manganese, E - selenium, N - nickel, C - silicon, F - vanadium, K - cobalt, C - zirconium.
The numbers appearing in the brand name after the letters indicate, as in the name of the structural steel grades, the percentage of the alloying element. Main characteristics of the mechanical properties of steels:
- E - modulus of elasticity - proportionality coefficient between normal stress and elongation;
- G - shear modulus (tangential elastic modulus) - proportionality coefficient between shear stress and relative shear;
- μ - Poisson's ratio - the absolute value of the ratio of transverse to longitudinal deformation in the elastic region;
- σт — yield strength (conditional) — the stress at which the residual deformation after removing the load is 0.2%;
- σв - temporary resistance (tensile strength) - tensile strength;
- δ - relative elongation - the ratio of the absolute residual elongation of the sample after rupture to the initial calculated length;
- hardness (HB, HRC, HV).
Young's modulus of elasticity and shear, Poisson's ratio values (Table)
Elastic properties of bodies
Below are reference tables for commonly used constants; if two of them are known, then this is quite sufficient to determine the elastic properties of a homogeneous isotropic solid.
Young's modulus or modulus of longitudinal elasticity in dyn/cm2.
Shear modulus or torsional modulus G in dyn/cm2.
Compressive modulus or bulk modulus K in dynes/cm2.
Compressibility volume k=1/K/.
Poisson's ratio µ is equal to the ratio of transverse relative compression to longitudinal relative tension.
For a homogeneous isotropic solid material, the following relationships between these constants hold:
G = E / 2(1 + μ) - (α)
μ = (E / 2G) - 1 - (b)
K = E / 3(1 - 2μ) - (c)
Poisson's ratio has a positive sign and its value is usually between 0.25 and 0.5, but in some cases it can go beyond these limits. The degree of agreement between the observed values of µ and those calculated using formula (b) is an indicator of the isotropy of the material.
Tables of Young's Modulus of Elasticity, Shear Modulus and Poisson's Ratio
Values calculated from relations (a), (b), (c) are given in italics.
| Material at 18°C | Young's modulus E, 1011 dynes/cm2. | Shear modulus G, 1011 dynes/cm2. | Poisson's ratio µ | Modulus of bulk elasticity K, 1011 dynes/cm2. |
| Aluminum | 7,05 | 2,62 | 0,345 | 7,58 |
| Bismuth | 3,19 | 1,20 | 0,330 | 3,13 |
| Iron | 21,2 | 8,2 | 0,29 | 16,9 |
| Gold | 7,8 | 2,7 | 0,44 | 21,7 |
| Cadmium | 4,99 | 1,92 | 0,300 | 4,16 |
| Copper | 12,98 | 4,833 | 0,343 | 13,76 |
| Nickel | 20,4 | 7,9 | 0,280 | 16,1 |
| Platinum | 16,8 | 6,1 | 0,377 | 22,8 |
| Lead | 1,62 | 0,562 | 0,441 | 4,6 |
| Silver | 8,27 | 3,03 | 0,367 | 10,4 |
| Titanium | 11,6 | 4,38 | 0,32 | 10,7 |
| Zinc | 9,0 | 3,6 | 0,25 | 6,0 |
| Steel (1% C) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (soft) | 21,0 | 8,12 | 0,291 | 16,78 |
| Constantan 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Manganin | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) For steel containing about 1% C, elastic constants are known to change during heat treatment. 2) 60% Cu, 40% Ni. |
The experimental results given below are for common laboratory materials, mainly wires.
| Substance | Young's modulus E, 1011 dynes/cm2. | Shear modulus G, 1011 dynes/cm2. | Poisson's ratio µ | Modulus of bulk elasticity K, 1011 dynes/cm2. |
| Bronze (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Copper | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Nickel silver1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Glass | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Glass yen crowns | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Jena flint glass | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Welding iron | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Cast iron | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Magnesium | 4,25 | 1,63 | 0,30 | — |
| Phosphor bronze2) | 12,0 | 4,36 | 0,38 | — |
| Platinoid3) | 13,6 | 3,6 | 0,37 | — |
| Quartz threads (floating) | 7,3 | 3,1 | 0,17 | 3,7 |
| Soft vulcanized rubber | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Steel | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Zinc | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92.5% Cu, 7% Sn, 0.5% P 3) Nickel silver with a small amount of tungsten. |
| Substance | Young's modulus E, 1011 dynes/cm2. | Substance | Young's modulus E, 1011 dynes/cm2. |
| Zinc (pure) | 9,0 | Oak | 1,3 |
| Iridium | 52,0 | Pine | 0,9 |
| Rhodium | 29,0 | Red tree | 0,88 |
| Tantalum | 18,6 | Zirconium | 7,4 |
| Invar | 17,6 | Titanium | 10,5-11,0 |
| Alloy 90% Pt, 10% Ir | 21,0 | Calcium | 2,0-2,5 |
| Duralumin | 7,1 | Lead | 0,7-1,6 |
| Silk threads1 | 0,65 | Teak | 1,66 |
| Web2 | 0,3 | Silver | 7,1-8,3 |
| Catgut | 0,32 | Plastics: | |
| Ice (-20C) | 0,28 | Thermoplastic | 0,14-0,28 |
| Quartz | 7,3 | Thermoset | 0,35-1,1 |
| Marble | 3,0-4,0 | Tungsten | 41,1 |
| 1) Reduces rapidly with increasing load 2) Detects noticeable elastic fatigue |
| Temperature coefficient (at 150C) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Compressibility k, bar-1 (at 7-110C) | |||
| ɑ, for E | ɑ, for G | |||
| Aluminum | 4,8*10-4 | 5,2*10-4 | Aluminum | 1,36*10-6 |
| Brass | 3,7*10-4 | 4,6*10-4 | Copper | 0,73*10-6 |
| Gold | 4,8*10-4 | 3,3*10-4 | Gold | 0,61*10-6 |
| Iron | 2,3*10-4 | 2,8*10-4 | Lead | 2,1*10-6 |
| Steel | 2,4*10-4 | 2,6*10-4 | Magnesium | 2,8*10-6 |
| Platinum | 0,98*10-4 | 1,0*10-4 | Platinum | 0,36*10-6 |
| Silver | 7,5*10-4 | 4,5*10-4 | Flint glass | 3,0*10-6 |
| Tin | — | 5,9*10-4 | German glass | 2,57*10-6 |
| Copper | 3,0*10-4 | 3,1*10-4 | Steel | 0,59*10-6 |
| Nickel silver | — | 6,5*10-4 | ||
| Phosphor bronze | — | 3,0*10-4 | ||
| Quartz threads | -1,5*10-4 | -1,1*10-4 |
Poisson's ratio values for some isotropic materials
| Aluminum | 0,34 |
| Tungsten | 0,29 |
| Germanium | 0,31 |
| Duralumin | 0,34 |
| Iridium | 0,26 |
| Quartz glass | 0,17 |
| Constantan | 0,33 |
| Brass | 0,35 |
| Manganin | 0,33 |
| Copper | 0,35 |
| Organic glass | 0,35 |
| Polystyrene | 0,35 |
| Lead | 0,44 |
| Tin | 0,44 |
| Silver | 0,37 |
| Gray cast iron | 0,22 |
| Steel | 0,28 |
| Glass | 0,25 |
| Porcelain | 0,23 |
Hooke's Law in Mathematical Form
Hooke's formulation, which we cited above, makes it possible to write it in the following form:
,
where the change in the length of a body due to compression or stretching, F is the force applied to the body and causes deformation (elastic force), k is the elasticity coefficient, measured in N/m.
It should be remembered that Hooke's law is valid only for small stretches.
We also note that it has the same appearance when stretched and compressed. Considering that force is a vector quantity and has a direction, then in the case of compression, the following formula will be more accurate:
, but again, it all depends on where the axis relative to which you are measuring will be directed.
What is the fundamental difference between compression and extension? Nothing if it is insignificant.
The degree of applicability can be considered as follows:
Let's pay attention to the graph. As we can see, with small stretches (the first quarter of the coordinates), for a long time the force with the coordinate has a linear relationship (red straight line), but then the real relationship (dotted line) becomes nonlinear, and the law ceases to be true
In practice, this is reflected by such strong stretching that the spring stops returning to its original position and loses its properties. With even greater stretching, a fracture occurs and the structure of the material is destroyed.
With small compressions (third quarter of the coordinates), for a long time the force with the coordinate also has a linear relationship (red line), but then the real relationship (dotted line) becomes nonlinear, and everything stops working again. In practice, this is reflected by such strong compression that heat begins to be released and the spring loses its properties. With even greater compression, the coils of the spring stick together and it begins to deform vertically, and then completely melt.
As you can see, the formula expressing the law allows you to find the force, knowing the change in the length of the body, or, knowing the elastic force, measure the change in length:
Also, in some cases, you can find the elasticity coefficient. To understand how this is done, consider an example task:
A dynamometer is connected to the spring. It was stretched using a force of 20 Newton, which is why it became 1 meter long. Then they released her, waited until the vibrations stopped, and she returned to her normal state. In normal condition, its length was 87.5 centimeters. Let's try to find out what material the spring is made of.
Given:
Solution:
Let's find the numerical value of the spring deformation:
Let's write down:
From here we can express the value of the coefficient:
Looking at the table, we can find that this indicator corresponds to spring steel.
Effect of radioactive irradiation on changes in mechanical properties
Radiation exposure affects different materials differently. Irradiation of materials of inorganic origin in its effect on mechanical characteristics and plasticity characteristics is similar to a decrease in temperature: with an increase in the dose of radioactive irradiation, the tensile strength and especially the yield strength increase, and the plasticity characteristics decrease.
Irradiation of plastics also leads to an increase in fragility, and irradiation has different effects on the tensile strength of these materials: on some plastics it has almost no effect (polyethylene), in others it causes a significant decrease in tensile strength (katamen), and in others it increases the tensile strength (selectron ).
Parameters on which the elasticity of wood depends
The modulus of elasticity of wood is a variable parameter, its value is influenced by:
- Humidity. The elasticity of wood is inversely related to humidity. That is, with high wood humidity, its ability to return to its original shape will be minimal.
- Straightness. If the fibers are arranged in a tortuous, random manner, then its ability to restore shape will be noticeably lower than that of a straight layer.
- Density. Low density wood is not as resilient as denser wood.
- Age of the tree. The wood of an old tree is more elastic than a young one.
- Natural features of wood. Coniferous trees have single-row small core rays, so their wood is more elastic, although the specific gravity of such species is not high.
- The age of the wood itself. The younger layers of the tree trunk are called sapwood, those that are located closer to the center, and, accordingly, older ones are called the core. The sapwood is more resilient than the heartwood.
Mechanical properties
Only when working in tension or compression does the (Young's) modulus of elasticity help to predict the behavior of a particular material. But for bending, shearing, crushing and other loads, you will need to enter additional parameters:
Read also: A device that looks for wires in the wall
- Stiffness is the product of the profile cross-section and the elastic modulus. By this value one can judge the plasticity of the structural unit as a whole, and not about the material separately. The unit of measurement is kilograms force.
- Longitudinal elongation is the ratio of the absolute elongation of the sample material to its total length. For example, some force was applied to a rod whose length is 200 millimeters. As a result, it became shorter by 5 millimeters. As a result, the relative elongation will be equal to 0.05. This quantity is dimensionless. For more convenient perception, it is sometimes converted into percentages.
- Transverse relative elongation is calculated in the same way as longitudinal relative elongation, but instead of length, the diameter of the rod is taken. It was experimentally found that for a larger amount of material, the transverse elongation is approximately 4 times less than the longitudinal elongation.
- Poisson's ratio. This is the ratio of relative longitudinal to relative transverse strain. Using this value, it is possible to fully describe the changes in shape under the influence of load.
- The shear modulus describes the elastic properties under the influence of tangential properties on the sample. In other words, when the force vector is directed towards the surface of the body at 90 degrees. An example of such loads is the work of nails under crushing, rivets under shear, etc. This parameter is related to the viscosity of the material.
- The bulk modulus of elasticity characterizes the change in the volume of a sample for a versatile uniform application of load. This value is the ratio of volumetric pressure to volumetric compressive strain. As an example, we can consider a material lowered into water, which is subject to liquid pressure over its entire area.
In addition to all of the above, it is worth mentioning that some materials have different mechanical properties depending on the direction of the load. Such materials are called anisotropic. Examples of this are fabrics, some types of stone, laminated plastics, wood, etc.
Isotropic materials have the same mechanical properties and elastic deformation in any direction. Such materials include metals: aluminum, copper, cast iron, steel, etc., as well as rubber, concrete, natural stones, non-laminated plastics.
Isotropic and anisotropic materials
Some materials are shear isotropic, meaning that the deformation in response to force is the same regardless of orientation. Other materials are anisotropic and respond differently to stress or strain depending on orientation. Anisotropic materials are much more susceptible to shear along one axis than the other. For example, consider the behavior of a block of wood and how it might respond to a force applied parallel to the grain of the wood compared to its response to a force applied perpendicular to the grain. Let's consider how a diamond reacts to an applied force. The rate of crystal shear depends on the orientation of the force relative to the crystal lattice.
Modulus of elasticity of plywood
Plywood is a building material made by gluing together several layers of wood veneer. She is very popular, and for good reason. In addition to aesthetic value, plywood has a number of parameters that distinguish it among materials for construction. After undergoing processing, plywood acquires strength, elasticity, and moisture resistance.
The characteristics of plywood are influenced by many factors:
- the type of wood used for veneer;
- initial state of raw materials;
- humidity of the plywood itself;
- the type and composition of the glue used to join the veneer layers;
- pre-treatment technology.
For plywood, the modulus of elasticity and all relevant coefficients are also calculated.
The important thing is that the modulus of elasticity of plywood and other indicators are higher than that of the wood from which it was made. The modulus of elasticity of wood must be calculated before constructing roofing and rafter systems.
Knowledge of the internal forces appearing in building materials is important for the safety and durability of the building. The ability to return a lost shape is significant when choosing the material for the handles of percussion instruments and weapon stocks
The modulus of elasticity of wood must be calculated before constructing roofing and rafter systems.
Knowledge of the internal forces appearing in building materials is important for the safety and durability of the building. The ability to return a lost shape is significant when choosing the material for the handles of percussion instruments and weapon stocks
General concept
The modulus of elasticity (also known as Young's modulus) is one of the indicators of the mechanical properties of a material, which characterizes its resistance to tensile deformation. In other words, its value shows the ductility of the material. The greater the elastic modulus, the less any rod will stretch, all other things being equal (load magnitude, cross-sectional area, etc.).
In the theory of elasticity, Young's modulus is denoted by the letter E. It is an integral part of Hooke's law (the law on the deformation of elastic bodies). Connects the stress arising in the material and its deformation.
According to the international standard system of units, it is measured in MPa. But in practice, engineers prefer to use the dimension kgf/cm2.
The elastic modulus is determined experimentally in scientific laboratories. The essence of this method is to tear dumbbell-shaped samples of material using special equipment. Having found out the stress and elongation at which the sample failed, divide these variables by each other, thereby obtaining Young's modulus.
Let us immediately note that this method is used to determine the elastic moduli of plastic materials: steel, copper, etc. Brittle materials - cast iron, concrete - are compressed until cracks appear.
Additional characteristics of mechanical properties
The modulus of elasticity makes it possible to predict the behavior of a material only when working in compression or tension. In the presence of such types of loads as crushing, shear, bending, etc., additional parameters will need to be introduced:
- Stiffness is the product of the elastic modulus and the cross-sectional area of the profile. By the value of rigidity, one can judge the plasticity not of the material, but of the structure as a whole. Measured in kilograms of force.
- Relative longitudinal elongation shows the ratio of the absolute elongation of the sample to the total length of the sample. For example, a certain force was applied to a rod 100 mm long. As a result, it decreased in size by 5 mm. Dividing its elongation (5 mm) by the original length (100 mm) we obtain a relative elongation of 0.05. A variable is a dimensionless quantity. In some cases, for ease of perception, it is converted to percentages.
- Relative transverse elongation is calculated similarly to the point above, but instead of length, the diameter of the rod is considered here. Experiments show that for most materials, transverse elongation is 3-4 times less than longitudinal elongation.
- The Punch ratio is the ratio of the relative longitudinal strain to the relative transverse strain. This parameter allows you to fully describe the change in shape under the influence of load.
- The shear modulus characterizes the elastic properties when the sample is exposed to tangential stresses, i.e., in the case when the force vector is directed at 90 degrees to the surface of the body. Examples of such loads are the work of rivets in shear, nails in crushing, etc. By and large, the shear modulus is associated with such a concept as the viscosity of the material.
- The bulk modulus of elasticity is characterized by a change in the volume of the material for uniform, versatile application of load. It is the ratio of volumetric pressure to volumetric compressive strain. An example of such work is a sample lowered into water, which is subject to liquid pressure over its entire area.
In addition to the above, it should be mentioned that some types of materials have different mechanical properties depending on the direction of loading. Such materials are characterized as anisotropic. Vivid examples are wood, laminated plastics, some types of stone, fabrics, etc.
Isotropic materials have the same mechanical properties and elastic deformation in any direction. These include metals (steel, cast iron, copper, aluminum, etc.), non-laminated plastics, natural stones, concrete, rubber.
see also
Modulus of bulk elasticity () | Young's modulus () | Lame parameters() | Shear modulus() | Poisson's Ratio () | en:P-wave modulus()
Wikimedia Foundation. 2010.
See what “Poisson’s ratio” is in other dictionaries:
Poisson's ratio - µ Coefficient of proportionality between the absolute values of the relative longitudinal ε1у and transverse ε2y elastic instantaneous deformations at s1 = 0.3 Rpr during axial compression of the sample Source: GOST 24452 8 ... Dictionary of terms for normative and technical documentation
Poisson's ratio is the absolute value of the ratio of transverse relative shortening (elongation) to relative longitudinal elongation (shortening) during simple tension (compression) of a straight rod within the limits of applicability of Hooke's law. [GOST 24452 80]… … Encyclopedia of terms, definitions and explanations of building materials
Poisson's ratio - µ The proportionality coefficient between the absolute values of the relative longitudinal ... Technical Translator's Guide
Poisson's ratio is an elastic constant of the material, equal to the ratio of the relative transverse deformation (ε2 and ε3) to the relative longitudinal deformation (ε1) under linear tension or compression: μ = ε2/ε1 = ε3/ε1 = const. Poisson's ratio of different... ... Encyclopedic Dictionary of Metallurgy
Poisson's ratio - Puasono santykis statusas T sritis Standartizacija ir metrologija apibrėžtis Tempiamo arba gniuždomo bandinio skersinės ir išilginės santykinių deformacijų dalmens absoliučioji vertė. atitikmenys: engl. Poisson number; Poisson's ratio vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Poisson's ratio - Puasono koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Tempiamų arba gniuždomų kūno sluoksnių skersinės ir išilginės deformacijų dalmens absoliučioji vertė. atitikmenys: engl. Poisson's ratio vok. Poisson Konstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Poisson's ratio - Puasono santykis statusas T sritis fizika atitikmenys: engl. Poisson number; Poisson's ratio vok. Poisson Constante, f; Poissonsche Konstante, f; Poissonsche Zahl, f rus. lateral compression ratio, m; Poisson's ratio, m pranc.… … Fizikos terminų žodynas
Poisson's ratio - Poisson's ratio Poisson's ratio. The absolute value of the ratio of transverse deformation to the corresponding longitudinal deformation, under conditions of uniformly distributed axial stress below Proportional limit Limit of proportionality... ... Dictionary of metallurgical terms
Poisson's ratio - Puasono koeficientas statusas T sritis fizika atitikmenys: engl. Poisson's ratio vok. Poisson Constante, f; Poissonscher Koeffizient, m rus. Poisson's ratio, m pranc. coefficient de Poisson, m; rapport de Poisson, m … Fizikos terminų žodynas
POISSON'S RATIO - the ratio of the relative lateral expansion of a test soil sample to its relative vertical deformation under the influence of a load under uniaxial compression. It is usually determined by the formula where £ is the coefficient of lateral soil pressure ... Dictionary of hydrogeology and engineering geology
Source