Young's modulus (modulus of elasticity) is a physical quantity that characterizes the properties of a material to bend or stretch under the influence of force; in fact, the rigidity of the body depends on this.
This is a property of any material, and it depends on the temperature and pressure applied.
In physics, elasticity is the property of solid materials to return to their original shape and size after the forces applied during deformation are removed.
In other words: when a body is deformed, a force appears that strives to restore the original shape and size of the body. The elastic force is this manifested force. It is also a consequence of electromagnetic interaction between particles.
A low value of Young's modulus means that the solid being studied is elastic .
A high value of Young's modulus means that the solid being studied is inelastic or rigid.
Examples of Young's modulus (elasticity) values for:
- (i.e. for rubber it is 5 times less than steel)
Table
Most materials have a very high order E value, so they are written using "gigapascals" ([GPa]; ).
| Material | Young's modulus E, [GPa] |
| Diamond | 1220 |
| Aluminum | 69 |
| Tree | 10 |
| Cadmium | 50 |
| Brass | 97 |
| Copper | 110 |
| Nickel | 207 |
| Rubber | 0.9 (≈ 1 MPa, megapascal) |
| Steel | 200 |
| Titanium | 107 |
Design resistances and elastic moduli for building materials
When calculating building structures, you need to know the design resistance and modulus of elasticity for a particular material.
Here is data on the main building materials. Table 1. Elastic moduli for basic building materials
| Material | Elastic modulus E, MPa |
| Cast iron white, gray | (1,15…1,60) · 105 |
| Malleable cast iron | 1,55 · 105 |
| Carbon steel | (2,0…2,1) · 105 |
| Alloy steel | (2,1…2,2) · 105 |
| Rolled copper | 1,1 · 105 |
| Cold drawn copper | 1,3 · 103 |
| Cast copper | 0,84 · 105 |
| Rolled phosphor bronze | 1,15 · 105 |
| Rolled manganese bronze | 1,1 · 105 |
| Cast aluminum bronze | 1,05 · 105 |
| Cold drawn brass | (0,91…0,99) · 105 |
| Rolled ship brass | 1,0 · 105 |
| Rolled aluminum | 0,69 · 105 |
| Aluminum wire drawn | 0,7 · 105 |
| Rolled duralumin | 0,71 · 105 |
| Rolled zinc | 0,84 · 105 |
| Lead | 0,17 · 105 |
| Ice | 0,1 · 105 |
| Glass | 0,56 · 105 |
| Granite | 0,49 · 105 |
| Lime | 0,42 · 105 |
| Marble | 0,56 · 105 |
| Sandstone | 0,18 · 105 |
| Granite masonry | (0,09…0,1) · 105 |
| Brick masonry | (0,027…0,030) · 105 |
| Concrete (see table 2) | |
| Wood along the grain | (0,1…0,12) · 105 |
| Wood across the grain | (0,005…0,01) · 105 |
| Rubber | 0,00008 · 105 |
| Textolite | (0,06…0,1) · 105 |
| Getinax | (0,1…0,17) · 105 |
| Bakelite | (2…3) · 103 |
| Celluloid | (14,3…27,5) · 102 |
Standard data for calculations of reinforced concrete structures
Table 2. Elastic moduli of concrete (according to SP 52-101-2003)
| Values of the initial modulus of elasticity of concrete in compression and tension Eb, MPa 10-3, with a concrete class for compressive strength | ||||||||||
| B10 | B15 | B20 | B25 | B30 | B35 | B40 | B45 | B50 | B55 | B60 |
| 19,0 | 24,0 | 27,5 | 30,0 | 32,5 | 34,5 | 36,0 | 37,0 | 38,0 | 39,0 | 39,5 |
Table 2.1 Elastic moduli of concrete according to SNiP 2.03.01-84*(1996)
Notes: 1. Above the line the values are indicated in MPa, below the line - in kgf/cm². 2. For lightweight, cellular and porous concrete at intermediate values of concrete density, the initial elastic moduli are taken by linear interpolation. 3. For non-autoclaved cellular concrete, the Eb values are taken as for autoclaved concrete, multiplied by a factor of 0.8. 4. For prestressing concrete, the values of Eb are taken as for heavy concrete, multiplied by coefficient a
= 0.56 + 0.006V.
Table 3. Standard values of concrete resistance (according to SP 52-101-2003) Table 4. Design values of concrete compression resistance (according to SP 52-101-2003) Table 4.1 Design values of concrete compression resistance according to SNiP 2.03.01-84*(1996) ) Table 5. Calculated values of concrete tensile strength (according to SP 52-101-2003) Table 6. Standard resistances for reinforcement (according to SP 52-101-2003) Table 6.1 Standard resistances for class A reinforcement according to SNiP 2.03.01-84* (1996) Table 6.2 Standard resistances for fittings of classes B and K according to SNiP 2.03.01-84* (1996) Table 7. Design resistances for fittings (according to SP 52-101-2003) Table 7.1 Design resistances for fittings of class A according to SNiP 2.03.01-84* (1996) Table 7.2 Design resistances for fittings of classes B and K according to SNiP 2.03.01-84* (1996)
Standard data for calculations of metal structures
Table 8. Standard and calculated resistances in tension, compression and bending (according to SNiP II-23-81 (1990)) of sheet, broad-band universal and shaped rolled products according to GOST 27772-88 for steel structures of buildings and structures
Notes: 1. For the thickness of the shaped rolled product should be taken as the thickness of the shelf (its minimum thickness is 4 mm).
2. The standard values of the yield strength and tensile strength in accordance with GOST 27772-88 are taken as standard resistance. 3. The values of the calculated resistances are obtained by dividing the standard resistances by the reliability factors for the material, rounded to 5 MPa (50 kgf/cm²). Table 9. Steel grades replaced by steels according to GOST 27772-88 (according to SNiP II-23-81 (1990))
Notes: 1. Steels C345 and C375 categories 1, 2, 3, 4 according to GOST 27772-88 replace steel categories, respectively 6, 7 and 9, 12, 13 and 15 according to GOST 19281-73* and GOST 19282-73*. 2. Steels S345K, S390, S390K, S440, S590, S590K according to GOST 27772-88 replace the corresponding steel grades of categories 1-15 according to GOST 19281-73* and GOST 19282-73*, indicated in this table. 3. Replacement of steels in accordance with GOST 27772-88 with steels supplied in accordance with other state all-Union standards and technical conditions is not provided.
Design resistances for steel used for the production of profiled sheets are not shown here.
Unit of measurement and formulas
The SI unit of Young's modulus is Newton per meter squared (N/m²), i.e. Pascal (Pa).
Formulas
There are several formulas from which you can calculate Young's modulus. For example, Hooke's law.
Hooke's law
You can calculate Young's modulus using these formulas (we will do this using an example). Because of this law, there are several interesting equalities that can be useful for calculations.
Hooke's law (this one describes phenomena in the body, in differential form):
Where:
- σ - mechanical stress
- E - Young's modulus (elastic modulus)
- ε—relative elongation
Hooke's Law (this one describes phenomena in the body)
Where:
- Fupr - elastic force
- k × Δl—body elongation
Where:
- Fupr - elastic force
- E - Young's modulus (elastic modulus)
- S - cross-sectional area
- l - initial body length
- Δl - body elongation
Where:
- Fpr/S - mechanical stress, denoted as σ
- Δl/l - relative elongation, denoted as ε
It should be noted that this law applies to the point where the material is irreversibly deformed and no longer returns to its original shape. At what point this happens depends on the material. If the material is very stiff (meaning a high elastic modulus reading), then this point may coincide with rupture/deformation.
Other formulas for calculating Young's modulus (elastic modulus)
Where:
- E - Young's modulus (elastic modulus)
- k - body stiffness
- l is the original length of the rod
- S - cross-sectional area
Or you can express k (body stiffness):
Where:
- k - body stiffness
- E - Young's modulus (elastic modulus)
- S - cross-sectional area
- l is the initial length of the rod/body
3. TEST METHODS
3.1. Tensile tests are carried out according to GOST 27208-87 on one sample.
3.2. Hardness determination is carried out according to GOST 27208-87.
3.3. Blanks for determining the mechanical properties of cast iron are cast according to GOST 24648-90.
3.4. When using heat treatment of castings, the workpieces must undergo heat treatment together with the castings to determine the mechanical properties.
It is allowed to use workpieces in a cast state (without heat treatment) when using low-temperature heat treatment to relieve linear stresses in castings.
3.5. If unsatisfactory test results are obtained, repeat tests are carried out on two samples.
The samples are considered to have passed the tests if the mechanical properties of each of them meet the requirements of this standard.
Areas of copper use
Due to its mechanical properties, copper has found wide application in various industries, but most often it can be found as an integral part of electrical wires, in heating and air cooling systems, in the production of computer equipment, and heat exchangers.
Industry uses thousands of tons of copper annually
In construction, this metal is used in the manufacture of various structures; the main advantage here is the low volumetric weight of copper. As noted above, non-ferrous metal has found wide application in roofing work, as well as in the manufacture of pipes. The resulting pipes are lightweight and can be transformed, which is especially important when designing water supply and sewerage systems.
The main part of the production of copper products is wire used as a core for electrical or communication cables. Due to the main characteristic of copper - electrical conductivity, it has a high resistance to current, and also has unique magnetic properties - unlike other metals, its particles do not react to a magnet, which sometimes complicates the process of cleaning it. It is worth noting that almost all production of products is based on the processing of secondary raw materials; ore is used extremely rarely.
Material tensile strength
This is the limit of the stress that occurs, after which the sample begins to fail.
Static tensile strength is measured under prolonged application of deforming force, dynamic - under short-term, impact nature of such force. For most substances the dynamic limit is greater than the static limit.
Tensile strength tool
In addition, there are limits to the material's compressive and tensile strength. They are determined experimentally on a test bench, by stretching or compressing samples with powerful hydraulic machines equipped with precise dynamometers and pressure meters. If it is impossible to achieve the required pressure hydraulically, a directed explosion in a sealed capsule is sometimes used.
Basic properties
Smelting copper from ore
Copper, as a metal, is obtained by smelting ore; in nature it is difficult to find pure nuggets; mainly enrichment and extraction is carried out from:
- chalcocite ore, in which the copper content is about 80%, this type is often called copper luster;
- Bronite ore, here the metal content is up to 65%
- covellite ore - up to 64%.
In terms of its physical properties, copper is a red-colored metal; a pink tint may be present in the section; it is classified as a heavy metal because it has a high density.
A distinctive characteristic is electrical conductivity. Due to this, the metal is widely used in the manufacture of cables and electrical wires. In this indicator, copper is second only to silver; in addition, there are a number of other physical characteristics:
- hardness - on the Brindel scale equals 35 kgf/mm²;
- elasticity - 132000 MN/m²;
- linear thermal expansion - 0.00000017 units;
- relative elongation - 60%;
- melting point - 1083 ºС;
- boiling point - 2600 ºС;
- thermal conductivity coefficient - 335 kcal/m*h*deg.
The main properties of copper include the elastic modulus, which is calculated by various methods:
The shear modulus is useful to know in the production of materials for the construction industry - it is a value that characterizes the degree of resistance to shear and deformation under the influence of various loads. The modulus calculated using Young's method shows how the metal will behave under uniaxial tension. The shear modulus characterizes the response of a metal to shear load. Poisson's ratio shows how a material behaves under uniform compression.
Development of mines for the extraction of copper and other metals
The chemical properties of copper describe the combination with other substances into alloys and possible reactions to an acidic environment. The most significant characteristic is oxidation. This process actively manifests itself during heating; already at a temperature of 375 ºC, copper oxide begins to form, or scale as it is called, which can affect the conductive functions of the metal and reduce them.
When copper reacts with a solution of an iron salt, it turns into a liquid state. This method is used to remove copper coating on various products.
Long stay in water causes cuprite
When copper is exposed to a humid environment for a long time, cuprite, a greenish coating, forms on its surface. This property of copper is taken into account when using metal to cover roofs. It is noteworthy that cuprite performs a protective function; the metal underneath does not deteriorate at all, even for a hundred years. The only opponents of copper roofs are environmentalists. They explain their position by the fact that when copper cuprite is washed off by rainwater into the soil or water bodies, it pollutes it with its toxins, which especially has a detrimental effect on microorganisms living in rivers and lakes. But to solve this problem, builders use drainpipes made of a special metal, which absorbs copper particles and accumulates them, while the water flows free of toxins.
Copper sulfate is another result of chemical action on metal. This substance is actively used by agronomists to fertilize the soil and stimulate the growth of various crops. However, uncontrolled use of vitriol can also have a detrimental effect on the environment. Toxins penetrate deep into the layers of the earth and accumulate in groundwater.
Types of loads
When using metals, different static and dynamic loads are applied. In the theory of strength, it is customary to define the following types of loads.
- Compression - an acting force compresses an object, causing a decrease in length along the direction of application of the load. This deformation is felt by frames, supporting surfaces, racks and a number of other structures that can withstand a certain weight. Bridges and crossings, car and tractor frames, foundations and reinforcement - all these structural elements are under constant compression.
- Tension - the load tends to lengthen the body in a certain direction. Lifting and transport machines and mechanisms experience similar loads when lifting and carrying loads.
- Shear and shear - such loading is observed in the case of forces directed along the same axis towards each other. Connecting elements (bolts, screws, rivets and other hardware) experience this type of load. The design of housings, metal frames, gearboxes and other components of mechanisms and machines necessarily contains connecting parts. The performance of devices depends on their strength.
- Torsion - if a pair of forces acting on an object are located at a certain distance from each other, then a torque occurs. These forces tend to produce torsional deformation. Similar loads are observed in gearboxes; the shafts experience just such a load. It is most often inconsistent in meaning. Over time, the magnitude of the acting forces changes.
- Bending – a load that changes the curvature of objects is considered bending. Bridges, crossbars, consoles, lifting and transport mechanisms and other parts experience similar loading.
Allowable tensile stress in some materials
From life experience we know that different materials resist changes in shape in different ways. The strength characteristics of crystalline and other solids are determined by the forces of interatomic interaction. As interatomic distances increase, the forces that attract atoms to each other also increase. These forces reach a maximum at a certain amount of stress, equal to approximately one tenth of Young's modulus.
This value is called theoretical strength; when it is exceeded, the destruction of the material begins. In reality, destruction begins at lower values, since the structure of real samples is heterogeneous. This causes an uneven distribution of stresses, and destruction begins from those areas where the stresses are maximum.
| Materials | σrast | |
| Bor | 5700 | 0,083 |
| Graphite | 2390 | 0,023 |
| Sapphire | 1495 | 0,030 |
| Steel wire | 415 | 0,01 |
| Fiberglass | 350 | 0,034 |
| Structural steel | 60 | 0,003 |
| Nylon | 48 | 0,0025 |
How is density determined?
The density of any substance is an indicator of the ratio of mass to total volume. The most common system for measuring density is kilogram per cubic meter. For copper this figure is 8.93 kg/m³. Since there are different grades of metal, which differ depending on the impurities of other substances, the overall density may vary. In this case, it is more appropriate to use another characteristic - specific gravity. In measuring systems, this indicator is expressed in different quantities:
Formula for determining the density of a substance
- SGS system - dyn/cm³;
- SI system - n/m³;
- MKSS system - kg/m³
In this case, the following formula can be used to convert values:
1 n/m³ = 1 dyne/cm³ = 0.102 kg/m³.
Specific gravity is an important indicator in the production of various materials containing copper, especially when it comes to its alloys. This is the ratio of the mass of copper to the total volume of the alloy.
You can consider how this indicator is used in practice using the example of calculating the weight of 25 copper sheets, 2000*1000 mm in size, 5 mm thick. First, let's determine the volume of the sheet - 5 mm * 2000 mm * 1000 mm = 10000000 mm3 or 10,000 cm³.
Specific gravity of copper 8.94 g/cm³
We calculate the weight of copper in one sheet - 10,000 * 8.94 = 89,400 g or 89.40 kg.
The mass of rolled copper in the total amount of material is 89.40 * 25 = 2,235 kg.
This calculation scheme is also used when processing scrap metal.
Methods for determining and monitoring strength indicators of metals
The development of metallurgy and other related areas for the production of metal objects is due to the creation of weapons. At first they learned to smelt non-ferrous metals, but the strength of the products was relatively low. Only with the advent of iron and its alloys did the study of their properties begin.
The first swords were made quite heavy to give them hardness and strength. Warriors had to take them in both hands to control them. Over time, new alloys appeared and production technologies were developed. Light sabers and swords came to replace heavy weapons. At the same time, tools were created. With increasing strength characteristics, tools and production methods were improved.
- Types of loads
- The concept of elastic modulus
- Table 1: Modulus of elasticity for metals and alloys
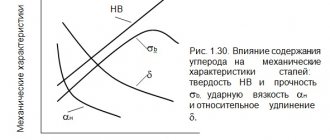
- Elastic modulus for different steel grades
- Table 2: Elasticity of steels
- Strength modules
- Table 3: Strength moduli for steels
Safety factor
To quantify the safety factor during design, a safety factor is used. It characterizes the product’s ability to withstand overloads above rated loads. For household products it is small, but for critical components and parts that, if destroyed, can pose a danger to human life and health, it is made multiple times.
Margin of safety
Accurate calculation of strength characteristics makes it possible to create a sufficient safety margin and at the same time not to overweight the structure, worsening its performance characteristics. For such calculations, complex mathematical methods and sophisticated software are used. The most important designs are calculated on supercomputers.
What is copper
One of the most common non-ferrous metals used in industry is copper, its Latin name is Cuprum, after the island of Cyprus, where it was mined by the Greeks many thousands of years ago. This is one of the seven metals that were known in ancient times; jewelry, dishes, money, and tools were made from it. Historians even called the period (from the 4th to the 3rd millennium BC) the Copper Age. D.I. Mendeleev put this metal in 29th place in his table, after hydrogen, since copper does not displace it from an acidic environment. Copper is a non-ferrous metal that has unique physical, mechanical, and chemical properties. The density of copper in kg m³ is one of the most important characteristics; it is used to determine the weight of the future product.