When people pass by surveyors working on the streets, construction sites, and garden plots, many wonder what kind of “tripod” this is, where to look into the device, and what will I see there? What is the name of this device, and why is it here? Often it is idle curiosity. Sometimes they just try to understand and understand how it works and what it measures. Some simply work in related industries and want to expand their horizons.
There are very complex systems and ultra-precise instruments that are rarely used, and in the ordinary life of an engineer you will not encounter them. Let's try to briefly talk about the instruments that are mainly used by surveyors in applied geodesy. About those tripods and “sticks” that surveyors carry around.
A short historical sketch
The famous Russian professor-geodesist, who lived and worked at the turn of the 19th and 20th centuries, Lieutenant General Vasily Vasilyevich Vitkovsky called his specialty one of the most useful areas of knowledge. In his opinion, humanity needs to study the shape and surface of the Earth just as much as each of us needs to know our own home in detail.
It is not surprising that geodesy is developing all the time and has long been aimed not only at our individual planet, but also at the entire solar system and even the galaxy in the future. Along with the development of civilization, this science became very complicated, divided into several disciplines - and, naturally, began to set itself and solve increasingly complex problems. Moreover, both theoretical due to the increase in the number and scale of research, and practical due to the increase in the number of unique engineering structures and structures. This could not but lead, on the one hand, to increased requirements for measurement accuracy, and on the other, to the complication of equipment. This has become especially noticeable in the last 10-20 years due to the rapid development of electronics and the beginning of the widespread use of lasers.
More information about the origins of geodesy as a science can be found in a special article devoted to this educational topic.
Total station
It’s clear that measuring angles, lengths and heights with different instruments is not very convenient and quite time consuming. Therefore, for those cases when it is necessary to carry out several types of measurements, there are combined instruments, such as a tacheometer. This is the most modern electro-optical device that allows you to measure any lengths, height differences and horizontal angles.
In most cases, this device is sufficient to record all necessary measurements on an object, provided that the accuracy of the device corresponds to the type of work. It is these devices, for the most part, that you can see on construction sites, on neighbors’ plots and along the roads of our country. At this stage of technology development, tacheometers are the most popular and universal instruments for carrying out geodetic measurements. Topographical surveys, land surveying and axes, for example, are impossible without a tacheometer.
History of invention
The origins of this mathematical instrument go back to the priests in Egypt and Babylon, who established the measure of angles in degrees, minutes and seconds. However, trigonometry was not used in mathematics until the times of classical Greece.
In the second century BC, the astronomer Hipparchus of Nikia invented a trigonometric table for measuring triangles. Then Ptolemy included in his great astronomical book, Almagest, a table with angular increments from 0 to 180°, with an error of less than 1/3600 units. He also explained the method for constructing this table, and throughout the book he gave many examples of how to calculate unknown elements of figures using it.
Ptolemy was also the author of the so-called Menelaus theorem for solving spherical triangles, and for many centuries his trigonometry was the main tool for astronomers.
Perhaps at the same time, the scientists of India also developed a trigonometric system based on the sine function, which, unlike the sine currently used, was not a proportion, but the length of the side opposite the angle in the right triangle of that hypotenuse. Indian mathematicians used different meanings for this in their tables.
Thomas Blundeville spoke about a device specially created for drawing and measuring figures in his “A Brief Description of Universal Charts” of 1589. As the name suggests, he used it to edit navigational charts for use in high latitudes.
Other European mathematicians also described similar devices around the same time. Regardless of who first invented the instrument, by the early 17th century it had become standard practice for navigators and surveyors. By the 18th century, protractors began to appear in textbooks on surveying and geometry.
Protractors in the modern sense arose in the second half of the 18th century, when scientists such as Jesse Ramsden and Georg Friedrich Brander improved previously created devices.
At that time, the preferred materials for their manufacture were:
- tree;
- brass;
- silver;
- copper;
- Ivory.
In the first half of the 20th century, tin and celluloid began to be used.
The device began to be called a protractor (Russian) in 1610. The term comes from the medieval word protractor, meaning “to carry,” which in turn comes from the Latin word protrahere, “to pull forward.”
Level
In many cases there is no need for bulkier and much more expensive and difficult to use total stations. In the construction of buildings, roads and other structures, after the planned location of the object is determined, you only need to control the height, level and verticality of the surfaces. The level easily copes with these functions. Its main task is to measure excesses between objects. There are electronic, optical, laser, auto-installation levels and others. In many cases, it is more convenient and expedient to use levels - for example, when monitoring settlements of buildings and structures, high-precision levels with automatic installation are used rather than total stations - again due to the high cost of the latter. To sum up the use of levels, we can say that most often they are used directly in the construction process due to their ease of use and relative cheapness.
GPS equipment
GPS modules or receivers accompany us in everyday life in our phones, navigators, tablets, etc. They are designed to help us navigate the area and not get lost in the urban jungle. However, they have little in common with geodetic GPS equipment.
Surveyors need these devices not for terrain orientation, but to accurately determine the location of the “dish” (usually the manufacturers of GPS receivers adhere to this form). The error is usually 0.5-2 centimeters relative to the nearest point of the State Geodetic Network (GGS). While conventional navigators give a location error of about 10-20 meters, which is unacceptable in the work of a surveyor. But there are many factors that very often negatively affect the magnitude of the error in geodetic measurements using GPS equipment. Therefore, it is not enough to simply purchase an expensive “dish” and start determining the location of neighboring fences, for example, like a regular navigator. Without proper calibration and subsequent processing of measurements, nothing will come of it.
In general, if you see a surveyor with a “dish” on a pole, know that he is determining the exact location of the point above which the receiver is located. Recently, the transfer of site boundaries to the terrain is carried out almost exclusively by the GPS method. It's much faster and more convenient.
Rulers. Bradis tables
To measure the value of a plane angle, it is enough to add another side to the angle so that a right triangle is formed. By measuring the sides of the resulting triangle, you can obtain the value of any trigonometric function of the angle whose value you need to know. Knowing the value of the sine, cosine, tangent or cotangent of an angle, you can use the Bradis table to find out the size of the angle. There are certain known angles that can be measured using a school square ruler. They produce two types of such rulers, both types are right-angled triangles made of wood, plastic or metal. The first type of square is an isosceles right triangle, two angles of which measure 45 degrees. The second type is a right triangle, one of the angles of which is 30 degrees, and the second is 60 degrees, respectively. By combining one of the vertices of the square with the vertex of the angle and the side with the side of the angle, when the other side of the angle coincides with the adjacent side of the square, you can find the corresponding value of the angle. Thus, using rulers-gons you can find angles of 30, 45, 60 and 90 degrees.
Tripod
A very simple surveyor's tool. Many people have encountered tripods when shooting photographs or films using professional equipment. Surveyors also use special equipment that cannot do without tripods. Geodesics differ from the rest mainly in their simplicity of design, ease of use and “indestructibility”. After all, you have to work in less than ideal conditions. The main task of a geodetic tripod is to immovably fix the device that is installed on it. First, a tribrach is placed on the tripod - a special device for centering over a certain point, if necessary, and leveling the device. Then a tacheometer, level, etc. device is installed. There are wooden, metal and composite tripods. Recently, the most “advanced” ones are fiberglass tripods. They are very light, durable... but so far unreasonably expensive.
Veshka
Also a fairly simple geodetic instrument. It looks like a round stick about 1.8m high. However, many poles are retractable and can be up to 6 meters high. At the top there can be both a reflector and a GPS receiver. The reflector can be of different shapes and designs. Its main task is to reflect the signal sent by the rangefinder. Its feature is that the beam/signal coming from the measuring device is reflected exactly back.
Ultimately, where the reflector or receiver is located on the geodetic pole, the location of the measured point is determined.
The magnitude of the angle and its measurement
Every angle has a magnitude. There is no special name for it in geometry.
Definition . The magnitude of an angle is a positive quantity defined for each angle so that: 1) equal angles have equal magnitudes; 2) if an angle consists of two angles, then its value is equal to the sum of the sizes of its parts.
These properties underlie the measurement of the angle. It is similar to measuring the length of a segment and consists of comparing the measured value of the angle with the value of the angle taken as a unit. The unit angle, and if necessary, its fractions, are plotted on the angle whose value is being measured. The result is a numerical value of the angle or a measure of the angle for a given unit of measurement.
The number that is obtained as a result of measuring the angle must satisfy a number of requirements - they are similar to the requirements for the numerical value of the length of a segment.
In practice, the unit of angle is a degree - part of a right angle. One degree is written as follows: 1°. The magnitude of a right angle is 90°, the magnitude of a reverse angle is 180°.
A degree is divided into 60 minutes, and a minute is divided into 60 seconds. One minute is denoted by 1′, one second by 1.” So, if the measure of the angle is 5 degrees 3 minutes and 12 seconds, then they write 5 ° 3'12 ". If greater accuracy is needed in measuring angle values, fractions of a second are used. Note that often instead of “angle value” they say “angle”. For example, instead of “the magnitude of the angle is 45 degrees,” they say that “the angle is 45 degrees.”
In practice, angles are measured using a protractor. For more accurate measurements, other instruments are also used.
The concept of the area of a figure and its measurement
Each person has an idea of what the area of a room is, the area of a piece of land, the area of surface that needs to be painted. He also understands that if the plots of land are the same, then their areas are equal; that the area of the apartment consists of the area of the rooms and the area of its other premises.
This common idea of area is used when defining it in geometry, where they talk about the area of a figure. But geometric figures are arranged in different ways, and therefore, when they talk about area, they single out a certain class of figures. For example, they consider the area of a polygon, the area of an arbitrary flat figure, the surface area of a polyhedron, etc. In our course we will only talk about the area of a polygon and an arbitrary flat figure.
Just as when considering the length of a segment and the magnitude of an angle, we will use the concept “consist of”, defining it as follows: figure F consists (composed) of figures F1 and F2, if it is their union and they do not have common internal points .
In the same situation, we can say that figure F is divided into figures F1 and F2. For example, about the figure F shown in Figure 2, a, we can say that it consists of figures F1 and F2, since they do not have common internal points. Figures F1 and F2 in Figure 2, b have common internal points, so it cannot be said that figure F consists of figures F1 and F2. If figure F consists of figures F1 and F2, then write: F=F1 Å F2.
Definition. The area of a figure is a positive quantity defined for each figure so that: 1) equal figures have equal areas; 2) if a figure consists of two parts, then its area is equal to the sum of the areas of these parts.
To measure the area of a figure, you need to have a unit of area. As a rule, such a unit is the area of a square with a side equal to a unit segment. Let us agree to denote the area of a unit square by the letter E, and the number that is obtained as a result of measuring the area of the figure - S(F). This number is called the numerical value of the area of the figure F with the selected unit of area E. It must satisfy the conditions:
1. The number S(F) is positive.
2. If the figures are equal, then the numerical values of their areas are equal.
3. If figure F consists of figures F1 and F2, then the numerical value of the area of the figure is equal to the sum of the numerical values of the areas of figures F1 and F2.
4. When replacing a unit of area, the numerical value of the area of a given figure F increases (decreases) by the same amount as the new unit is smaller (larger) than the old one.
5. The numerical value of the area of a unit square is taken equal to 1, i.e. S(F) = 1.
6. If figure F1 is part of figure F2, then the numerical value of the area of figure F1 is not greater than the numerical value of the area of figure F2, i.e. F1 Ì F2 Þ S (F1) ≤ S (F2) .
In geometry it has been proven that for polygons and arbitrary plane figures such a number always exists and is unique for each figure.
Figures whose areas are equal are called equal in area.
Area of a polygon
Formulas for calculating the area of a rectangle, triangle, and parallelogram were derived a long time ago. In geometry, they are justified based on the definition of area, with the numerical value of the area being called area, and the numerical value of the length of a segment being called length.
Theorem.
The area of a rectangle is equal to the product of the lengths of its adjacent sides.
Let us recall that the word “area” in this formulation means the numerical value of the area, and the word “length” means the numerical value of the length of the segment.
Proof. If F is a given rectangle, and the numbers a, b are the lengths of its sides, then S(F) = a ∙ b. Let's prove it.
Let a and b be natural numbers. Then the rectangle F can be divided into unit squares (Fig . 3): F = E Å E Å E Å … Å E. There are a∙b in total, since we have b rows, each of which has a squares. Hence S(F) = S(E)+S(E)+…+S(E)= a∙b∙S(E) = a∙b
Let now a and b be positive rational numbers: a = , b = , where m, n, p, q are natural numbers.
Let's bring these fractions to a common denominator: a = , b = . Let us divide the side of the unit square E into nq equal parts. If straight lines parallel to the sides are drawn through the division points, then square E will be divided into (nq)2 smaller squares. Let us denote the area of each such square as E1. Then S(E) = (nq)2 ∙ S(E1), and since S(E)=1, then S(E1) =
Since a = , b = , then a segment of length fits on side a exactly mq times, and on side b exactly mq times. Therefore, this rectangle F will consist of mq ∙ np squares E1. Hence,
S(F) = mq ∙ np ∙ S(E1) = mq ∙ np ∙ = = = a ∙ b
Thus, it is proven that if the lengths of the sides of a rectangle are expressed by positive rational numbers a and b, then the area of this rectangle is calculated by the formula S(P) = a ∙ b.
We omit the case when the lengths of the sides of the rectangle are expressed as positive real numbers.
A corollary follows from this theorem: the area of a right triangle is equal to half the product of its legs.
Theorem.
The area of a parallelogram is equal to the product of its side and the height drawn to that side .
Proof.
Let ABCD be a parallelogram that is not a rectangle (Fig. 4). Let us lower the perpendicular CE from vertex C to line AD. Then S(ABCE) = S(ABCD) + S(CDE).
Let us drop a perpendicular ВF from vertex B to line AD. Then S(ABCE) = S(ALLF) + S(ABF).
Since triangles ABF and CDE are equal, their areas are also equal.
It follows that S(ABCD) = S(ALLF), i.e. The area of the parallelogram ABCD is equal to the area of the rectangle BCEF and is equal to BC∙BF, and since BC = AD, then S(ABCD) = AD∙BF.
A corollary follows from this theorem: the area of a triangle is equal to half the product of its side and the height drawn to it.
Note that the words “side” and “height” in these statements denote the numerical values of the lengths of the corresponding segments.
Theorem.
The area of a regular polygon is equal to half the product of its perimeter and the radius of the inscribed circle.
If the perimeter of a regular polygon is denoted by the letter P, the radius of the inscribed circle is r, and the area of a regular polygon is S, then, according to this theorem, S = P ∙r.
Proof.
Let us divide a regular n-gon into n triangles, connecting the vertices of the n-gon with the center of the inscribed circle with segments (Fig. 5). These
triangles are equal. The area of each of them is equal to ∙r, where аn is the side of a regular n-gon. Then the area of the polygon is ∙r∙n, but an ∙ n = P. Therefore, S =
If F —
arbitrary polygon, then its area is found by dividing the polygon into triangles (or other figures for which the rules for calculating the area are known). In this regard, the question arises: if the same polygon is divided into parts in different ways and their areas are found, will the resulting sums of the areas of the parts of the polygon be the same? It has been proven that the conditions formulated in the definition of area, the area of any polygon is uniquely determined.
In addition to the equality and equal size of figures in geometry, the relation of equal composition is considered. Important properties of figures are associated with it.
Polygons F1 and F2 are called equiconstituted ,
if they can be divided into correspondingly equal parts.
For example, the parallelogram ABCD and the rectangle FBCE are equivalent (Fig. 4), since the parallelogram consists of figures F1 and F2, and the rectangle consists of figures F2 and F3, and F1 = F3.
It is not difficult to verify that equally composed figures are equal in size.
The Hungarian mathematician F. Bolyai and the German mathematics lover P. Gerwin proved the theorem: any two equal-sized polygons are equivalent. In other words, if two polygons have equal areas, then they can always be represented as consisting of pairs of equal parts.
The Bolyai-Gerwin theorem serves as a theoretical basis for solving problems of reshaping shapes: cutting one into pieces and folding it into another. It turns out that if these figures are polygonal and have the same areas, then the problem is certainly solvable.
The proof of the Bolyai-Gerwin theorem is quite complex. We will only prove the statement that every triangle is equivalent to a certain rectangle, i.e. Any triangle can be redrawn into a rectangle of equal size.
Let triangle ABC be given (Fig. 6). Let us draw the height BD and the center line KL in it. Let's construct a rectangle, one side of which is AC, and the other lies on the line KL. Since the pairs of triangles ARK and KBT, as well as CLM and TVL are equal, then triangle ABC and rectangle ARMC are equal.
5. Area of an arbitrary flat figure and its measurement
We found out that calculating the area of a polygon essentially comes down to calculating the areas of the triangles into which this polygon can be divided. How to find the area of an arbitrary flat figure? And what is the number that expresses this area?
Let F be an arbitrary plane figure. In geometry, it is considered to have area S(F) if the following conditions are met; there are polygonal figures that contain F (let's call them enclosing); there are polygonal figures that are contained in F (let's call them incoming); the areas of these polygonal figures differ as little as possible from S(F). Let us explain these provisions. Figure 7 shows that the figure Q contains the figure P, i.e. Q is an enclosing figure, and the figure P is contained in F, i.e. R - incoming figure. In set-theoretic language this means that and, therefore, we can write that .
If the difference between the areas of the enclosing and incoming figures can become as small as desired, then, as has been established in mathematics, there is a unique number S(F) that satisfies the inequality for any polygonal figures P and Q. This number is considered the area of the figure F.
These theoretical principles are used, for example, when deriving the formula for the area of a circle. To do this, a regular n-gon P is inscribed in a circle F of radius r, and a regular n-gon Q is described around the circle. If we denote the areas of these polygons by the symbols S(Q) and S(P), then we will have that , and as the number increases of the sides of inscribed and circumscribed polygons, the areas S(P) will increase, while remaining less than the area of the circle, and the areas S(Q) will decrease, but remain greater than the area of the circle.
The area of a regular n-gon is equal to half the product of its perimeter and the radius of the circle inscribed in it. As the number of its sides increases, the perimeter tends to the circumference, and the area tends to the area of the circle. Therefore Scr = = r 2.
To approximately measure the areas of flat figures, you can use various devices, in particular, a palette.
A palette is a transparent plate on which a network of squares is applied. The side of a square is taken as 1, and the smaller this side, the more accurately the area of the figure can be measured.
We apply the palette to this figure F. The squares that lie entirely inside the figure F form a polygonal figure P; squares that have common points with the figure F and lie entirely inside the figure F form a polygonal figure Q (Fig. 8). The areas S(P) and S(Q) are found by simply counting squares. The arithmetic mean of the found areas is taken as the approximate value of the area of figure F:
S(F) = .
In the initial mathematics course, students measure the areas of figures using a palette in this way: count the number of squares that lie inside the figure F and the number of squares through which the contour of the figure passes; then the second number is divided in half and added to the first. The resulting amount is considered the area of figure F.
It is not difficult to justify these actions. Let m be the number of squares that fit inside the figure F, and n the number of squares through which the contour of the figure F passes. Then S(P) = m, and S(Q) = m + n.
And that means S(F) = = =
The palette allows you to measure the area of the F shape with a certain accuracy. To get a more accurate result, you need to take a palette with smaller squares. But you can do it differently: apply the same palette to the figure in different ways and find several approximate values for the area of the figure F. Their arithmetic average may be the best approximation to the numerical value of the area of the figure F.
Laser roulette
It appeared relatively recently in geodetic teams, as previously it was quite expensive and difficult to use. And to this day it is not the only device for directly measuring distances on an object. Convenient to use over short distances and indoors. It is not often used in outdoor conditions, since it is necessary to have a surface onto which the laser beam can be aimed. Another disadvantage of many models without an optical sight is the poor visibility of the laser dot on brightly lit surfaces.
In view of this, it is now still quite common to use steel tape measures up to 50m long. Longer lengths are not available, so distances greater than 50 meters are sources of error due to several measurement steps. Measurements need to be carried out together, and the sagging of the tape causes some error in the measurements.
As a result, laser tape measures are used everywhere by cadastral engineers and surveyors in cases where it is appropriate and possible. Almost all measurements of premises for examination of premises or technical plans cannot be done without it. In other cases, a good old steel tape measure helps.
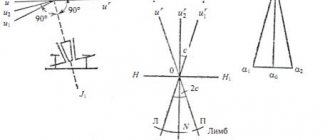
Theodolite
The tools listed in the previous paragraphs are used to measure angles on a plane. In practice - in geodesy, construction, topography - a special device is used to measure the so-called horizontal and vertical angles called a theodolite. The main measuring elements of a theodolite are special cylindrical rings (limbs), on which degree markings are evenly applied. Installed using a special stand at the top of the corner, the device is aimed using a telescope, first at a point located on one side of the corner where the measurement is made, then on the other side of the corner, and the measurement is taken again. The difference in measurements determines the angle in the first half-step. Then the second half-reception is performed - in the opposite direction. The arithmetic mean of the values obtained in two half-steps is the value of the measured angle.
Pipe cable detector
A device accompanying engineering and geodetic surveys for plotting underground communications on the plan. Often the kit includes a generator that is installed on the communication in its visible part. It generates vibrations that are detected by the receiver. After identifying the turning points of communications, they are applied to the geobase or topographic plan. The cable detector can also measure the depth of communications with an accuracy of 0.01 m.
check
We told you briefly about geodetic instruments and tools needed in applied geodesy. We hope that we have helped you understand the intricacies of tripods and “sticks” with which people who call themselves surveyors work.
Get acquainted with the cost of our work