Как выглядит линейка для измерения углов: виды и варианты представления результатов измерений

Когда люди проходят мимо геодезистов, работающих на улицах, стройках, на садовых участках, многие задаются вопросом- а что это за «тренога» такая, куда посмотреть в прибор, а что я там увижу? Как называется этот прибор, и зачем он здесь стоит? Часто-это праздное любопытство. Иногда просто пытаются вникнуть и понять, как это действует и что меряет. Некоторые просто работают в смежных отраслях и хотят расширить свой кругозор.

Существуют очень сложные системы и сверхточные приборы, которые редко используются, и в обычной жизни инженера Вы с ними не встретитесь. Попробуем вкратце рассказать про приборы, которые, в основном, используют геодезисты в прикладной геодезии. Про те штативы и «палочки», с которыми ходят геодезисты.

Небольшой исторический очерк

Известный российский профессор-геодезист, который жил и работал на рубеже XIX и XX столетий, генерал-лейтенант Василий Васильевич Витковский свою специальность называл одной из самых полезных областей знания. По его мнению, изучать форму и поверхность Земли человечеству необходимо настолько же, насколько каждому из нас — в подробностях узнать собственный дом.

Неудивительно, что геодезия всё время развивается и уже давно нацелилась не только на нашу отдельную планету, а и на всю Солнечную систему и даже галактику в перспективе. Вместе с развитием цивилизации эта наука очень усложнилась, разделилась на несколько дисциплин — и, естественно, начала ставить перед собой и решать всё более сложные задачи. Причём как теоретические по причине роста количества и масштабов исследований, так и практические — из-за увеличения числа уникальных инженерных конструкций и сооружений. Это не могло не привести, с одной стороны к повышению требований к точности измерений, а с другой — к усложнению оборудования. Особенно сильно это стало заметно в последние 10-20 лет в связи со стремительным развитием электроники и началом широкого применения лазеров.

Подробнее про зарождение геодезии, как науки, можно узнать в специальной статье, посвященной этой познавательной теме.

Тахеометр

Понятное дело, измерять углы, длины и высоты разными приборами — не слишком удобно и довольно долго к тому же. Поэтому для тех случаев, когда нужно проводить несколько типов измерений, существуют приборы комбинированные, такие как тахеометр. Это наиболее современный электронно-оптический прибор, который позволяет измерять любые длины, разницы высот и горизонтальные углы.

В большинстве случаев этого прибора достаточно для фиксации всех необходимых измерений на объекте, при условии, что точность прибора соответствует виду работ. Именно подобные приборы, в большинстве своем, Вы можете видеть на стройплощадках, на участках соседей и вдоль дорог нашей страны. Тахеометры на данном этапе развития технологий являются наиболее востребованными и универсальными приборами для проведения геодезических измерений. Топографические съемки, межевание и разбивка осей , например без тахеометра невозможна.

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.

Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.

Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.

Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.

В то время предпочтительными материалами для их изготовления были:

• дерево;
• латунь;
• серебро;
• медь;
• слоновая кость.

В первой половине XX века начали применять олово и целлулоид.

Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».

Нивелир

Во многих случаях нет необходимости в более громоздких и намного более дорогих и сложных в использовании тахеометрах. В строительстве зданий, дорог и других сооружений после планового определения местоположения объекта нужно лишь контролировать высоту, уровень и вертикальность поверхностей. С этими функциями легко справляется нивелир. Его основная задача — измерять превышения между объектами. Бывают нивелиры электронные, оптические, лазерные, с автоустановкой и прочие. Во многих случаях нивелиры использовать удобнее и целесообразнее —например, при наблюдении за осадками зданий и сооружений используются высокоточные нивелиры с автоустановкой, нежели тахеометры- опять же из-за дороговизны последних. Подводя некую черту по использованию нивелиров, можно сказать, что чаще всего они используются непосредственно в процессе строительства из- за простоты использования и относительной дешевизны.

GPS оборудование

GPS модули или приемники сопутствуют нам в повседневной жизни в наших телефонах, навигаторах, планшетах и т.д. Они призваны помочь нам сориентироваться на местности и не потеряться в городских джунглях. Однако они имеют мало общего с геодезическим GPS оборудованием.

Геодезистам эти приборы нужны не для ориентирования на местности, а для точного определения местоположения «тарелки» (обычно такой формы придерживаются производители GPS приемников). Погрешность обычно составляет 0,5-2 сантиметра относительно ближайшего пункта Государственной Геодезической Сети (ГГС). В то время, как обычные навигаторы дают ошибку местоположения около 10-20 метров, что в работе геодезиста недопустимо. Но есть множество факторов, которые весьма часто негативно влияют на величину погрешности геодезических измерений при помощи GPS оборудования. Поэтому недостаточно просто приобрести дорогостоящую «тарелку», и начать определять местоположение соседних заборов, например, как обычным навигатором. Без должной калибровки и последующей обработки измерений ничего не выйдет.

В общем, если увидите геодезиста с «тарелкой» на вешке, знайте- он определяет точное местоположение точки, над которой стоит приемник. В последнее время вынос границ участка на местность производится практически только GPS методом. Это гораздо быстрее и удобнее.

Линейки. Таблицы Брадиса

Для измерения величины плоского угла достаточно дополнить угол еще одной стороной так, чтобы образовался прямоугольный треугольник. Измерив величины сторон полученного треугольника, можно получить значение любой тригонометрической функции угла, величину которого необходимо узнать. Зная значение синуса, косинуса, тангенса или котангенса угла, можно, воспользовавшись таблицей Брадиса, узнать величину угла. Есть определенные известные величины углов, которые можно измерить с помощью школьной линейки-угольника. Выпускают два вида таких линеек, оба вида представляют из себя прямоугольные треугольники, выполненные из дерева, пластика или металла. Первый вид угольника — равнобедренный прямоугольный треугольник, два угла которого имеют величину 45 градусов. Второй вид — прямоугольный треугольник, один из углов которого равен 30 градусам, а второй — 60 градусам соответственно. Совместив одну из вершин угольника с вершиной угла и сторону — со стороной угла при совпадении другой стороны угла со смежной стороной угольника можно найти соответствующую величину угла. Таким образом, с помощью линеек-угольников можно найти величины углов в 30, 45, 60 и 90 градусов.

Штатив

Очень простой инструмент геодезиста. Многие сталкивались со штативами при съемках фотографий или фильмов с использованием профессионального оборудования. Геодезисты также пользуются специальным оборудованием, которое без штативов обойтись не может. От остальных геодезические отличаются в основном простотой конструкции, неприхотливостью в использовании и «неубиваемостью». Ведь работать приходится совсем не в идеальных условиях. Основная задача геодезического штатива- неподвижно зафиксировать прибор, который на него устанавливается. На штатив сначала ставится трегер- специальное устройство для центрирования над определенной точкой при необходимости и горизонтирования прибора. Потом уже ставится прибор-тахеометр, нивелир и т.д. Различают деревянные, металлические и штативы из композитных материалов. В последнее время самыми «продвинутыми» являются штативы из фибергласса. Они очень легкие, прочные..но пока что неоправданно дорогие.

Вешка

Тоже достаточно простой геодезический инструмент. Выглядит как круглая палка высотой около 1.8м. Однако многие вешки раздвигаются и могут иметь высоту до 6 метров. Наверху может находиться как отражатель, так и GPS приемник. Отражатель может быть разной формы и конструкции. Главная его задача- отражать сигнал, посланный дальномером. Его особенностью является то, что луч/сигнал, приходящий с прибора-измерителя отражается точно обратно.

В конечном итоге-там где находится отражатель или приемник на геодезической вешке происходит определение местоположения измеряемой точки.

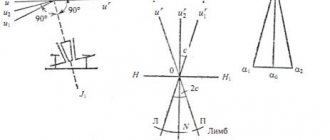
Величина угла и ее измерение

Каждый угол имеет величину. Специального названия для нее в геометрии нет.

Определение. Величиной угла называется положительная величина, определенная для каждого угла так, что: 1) равные углы имеют равные величины; 2) если угол состоит из двух углов, то его величина равна сумме величин его частей.

Эти свойства лежат в основе измерения величины угла. Оно аналогично измерению длины отрезка и состоит в сравнении измеряемой величины угла с величиной угла, принятой за единицу. Единичный угол, а если нужно и его доли, откладываются на угле, величина кото­рого измеряется. В результате получается численное значение величины угла или мера величины угла при данной единице измерения.

Число, которое получается в результате измерения величины угла, должно удовлетворять ряду требований — они аналогичны требованиям, предъявляемым к числовому значению длины отрезка.

На практике за единицу величины угла принимают градус — часть прямого угла. Один градус записывают так: 1°. Величина прямого угла равна 90°, величина развернутого — 180°.

Градус делится на 60 минут, а минута на 60 секунд. Одну минуту обозначают 1′, одну секунду – 1». Так, если мера величины угла равна 5 градусам 3 минутам и 12 секундам, то пишут 5°3’12». Если нужна большая точность в измерении величин углов, используют и доли секунды. Заметим, что часто вместо «величина угла» говорят «угол». Например, вместо «величина угла равна 45 градусам» говорят, что «угол равен 45 градусам».

На практике величины углов измеряют с помощью транспортира. Для более точных измерений пользуются и другими приборами.

Понятие площади фигуры и ее измерение

Каждый человек представляет, что такое площадь комнаты, площадь участка земли, площадь поверхности, которую надо покрасить. Он также понимает, что если земельные участки одинаковы, то площади их равны; что площадь квартиры складывается из площади комнат и площади других ее помещений.

Это обыденное представление о площади используется при ее определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому, когда говорят о площади, выделяют определенный класс фигур. Например, рассматривают площадь многоугольника, площадь произвольной плоской фигуры, площадь поверхности многогранника и др. В нашем курсе речь будет идти только о площади многоугольника и произвольной плоской фигуры.

Так же, как и при рассмотрении длины отрезка и величины угла, будем использовать понятие «состоять из», определяя его следующим образом: фигура F состоит (составлена) из фигур F1 и F2, если она является их объединением и у них нет общих внутренних точек.

В этой же ситуации можно говорить, что фигура F разбита на фигуры F1 и F2. Например, о фигуре F, изображенной на рисунке 2, а, можно сказать, что она состоит из фигур F1 и F2, поскольку они не имеют общих внутренних точек. Фигуры F1 и F2 на рисунке 2, b имеют общие внутренние точки, поэтому нельзя утверждать, что фигура F состоит из фигур F1 и F2. Если фигура F состоит из фигур F1 и F2, то пишут: F=F1 Å F2.

Определение.Площадью фигуры называется положительная величина, определенная для каждой фигуры так, что: 1) равные фигуры имеют равные площади; 2) если фигура состоит из двух частей, то ее площадь равна сумме площадей этих частей.

Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, такой единицей является площадь квадрата со стороной, равной единичному отрезку. Условимся площадь единичного квадрата обозначать буквой Е, а число, которое получается в результате изме­рения площади фигуры – S(F). Это число называют численным значе­нием площади фигуры F при выбранной единице площади Е. Оно должно удовлетворять условиям:

1. Число S(F) — положительное.

2. Если фигуры равны, то равны численные значения их площадей.

3. Если фигура F состоит из фигур F1 и F2, то численное значение площади фигуры равно сумме численных значений площадей фигур F1 и F2.

4. При замене единицы площади численное значение площади данной фигуры F увеличивается (уменьшается) во столько же раз, во сколько новая единица меньше (больше) старой.

5. Численное значение площади единичного квадрата принимается равным 1, т.е. S(F) = 1.

6. Если фигура F1 является частью фигуры F2, то численное значе­ние площади фигуры F1 не больше численного значения площади фи­гуры F2, т.е. F1 Ì F2 Þ S (F1) ≤ S (F2) .

В геометрии доказано, что для многоугольников и произвольных плоских фигур такое число всегда существует и единственно для каждой фигуры.

Фигуры, у которых площади равны, называются равновеликими.

Площадь многоугольника

Формулы для вычисления площади прямоугольника, треугольника, параллелограмма были выведены давно. В геометрии их обосновывают, исходя из определения площади, при этом численное значение площади называют площадью, а численное значение длины отрезка — длиной.

Теорема.
Площадь прямоугольника равна произведению длин соседних его сторон.
Напомним, что слово «площадь» в этой формулировке означает численное значение площади, а слово «длина» — численное значение длины отрезка.

Доказательство. Если F — данный прямоугольник, а числа a, b — длины его сторон, то S(F) = a ∙ b. Докажем это.

Пусть а и b — натуральные числа. Тогда прямо­угольник F можно разбить на единичные квадраты (рис. 3): F = Е Å Е Å Е Å … Å Е. Всего их а∙b, так как имеем b рядов, в каждом из которых а квадратов. Отсюда S(F) = S(E)+S(E)+…+S(E)= a∙b∙S(E) = a∙b

Пусть теперь a и b — положительные рациональные числа: а = , b = , где m, n, p, q — натуральные числа.

Приведем данные дроби к общему знаменателю: а = , b = . Разобьем сторону единичного квадрата Е на nq равных частей. Если через точки деления провести прямые, параллельные сторонам, то квадрат Е разделится на (пq)2 более мелких квадратов. Обозначим площадь каждого такого квадрата Е1. Тогда S(Е) = (пq)2 ∙ S(E1), а по­скольку S(Е)=1, то S(E1) =

Так как а = , b = , то отрезок длиной укладывается на стороне a точно mq раз, а на стороне b — точно пр раз. Поэтому дан­ный прямоугольник F будет состоять из mq ∙ np квадратов Е1. Следо­вательно,

S(F) = mq ∙ np ∙ S(E1) = mq ∙ np ∙ = = = a ∙ b

Таким образом доказано, что если длины сторон прямоугольника выражены положительными рациональными числами а и b, то пло­щадь этого прямоугольника вычисляется по формуле S(Р) = а ∙ b.

Случай, когда длины сторон прямоугольника выражаются поло­жительными действительными числами, мы опускаем.

Из этой теоремы вытекает следствие: площадь прямоугольного треугольника равна половине произведения его катетов.

Теорема.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Доказательство.

Пусть АВСD — параллелограмм, не являющийся прямоугольником (рис. 4). Опустим перпендикуляр СЕ из вершины С на прямую АD. Тогда S(АВСЕ) =S(АВСD) + S(СDЕ).

Опустим перпендикуляр ВF из вершины В на прямую АD. Тогда S(АВСЕ) = S(ВСЕF) + S(АВF).

Так как треугольники АВF и СDЕ равны, то равны и их площади.

Отсюда следует, что S(АВСD) = S(ВСЕF), т.е. площадь параллелограмма АВСD равна площади прямоугольника ВСЕF и равна ВС∙ВF, а так как ВС = АD, то S(АВСD) = АD∙ВF.

Из этой теоремы вытекает следствие: площадь треугольника равна половине произведения его стороны на проведенную к ней высоту.

Заметим, что слова «сторона» и «высота» в данных утверждениях обозначают численные значения длин соответствующих отрезков.

Теорема.
Площадь правильного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
Если периметр правильного многоугольника обозначить буквой Р, радиус вписанной окружности — r, а площадь правильного многоугольника — S, то, согласно данной теореме, S = Р ∙r.

Доказательство.

Разобьем правильный n-угольник на п треугольников, соединяя отрезками вершины n-угольника с центром вписанной окружности (рис.5). Эти

треугольники равны. Площадь каждого из них равна ∙r, где аn — сторона правильного n-угольника. Тогда площадь многоугольника равна ∙r∙n, но an ∙ n = Р. Следовательно, S =

Если F —

произвольный многоугольник, то его площадь находят, разбивая многоугольник на треугольники (или другие фигуры, для которых известны правила вычисления площади). В связи с этим возникает вопрос: если один и тот же многоугольник по-разному разбить на части и найти их площади, то будут ли получен­ные суммы площадей частей многоугольника одинаковыми? Доказа­но, что условиями, сформулированными в определении площади, площадь всякого многоугольника определена однозначно.

Кроме равенства и равновеликости фигур в геометрии рассматривают отношение равносоставленности. С ним связаны важные свойства фигур.

Многоугольники F1 и F2 называются равносоставленными,

если их можно разбить на соответственно равные части.

Например, равносоставлены параллелограмм АВСD и прямоугольник FВСЕ (рис. 4), так как параллелограмм состоит из фигур F1 и F2, а прямоугольник — из фигур F2 и F3, причем F1 = F3.

Нетрудно убедиться в том, что равносоставленные фигуры равно­велики.

Венгерским математиком Ф.Бойяи и немецким любителем мате­матики П.Гервином была доказана теорема: любые два равновеликих многоугольника равносоставлены.Другими словами, если два многоугольника имеют равные площади, то их всегда можно представить состоящими из попарно равных частей.

Теорема Бойяи-Гервина служит теоретической базой для решения задач на перекраивание фигур: одну разрезать на части и сложить из нее другую. Оказывается, что если данные фигуры многоугольные и имеют одинаковые площади, то задача непременно разрешима.

Доказательство теоремы Бойяи-Гервина достаточно сложное. Мы докажем только утверждение о том, что всякий треугольник равносоставлен с некоторым прямоугольником, т.е. всякий треугольник можно перекроить в равно­великий ему прямоугольник.

Пусть дан треугольник АВС (рис. 6). Проведем в нем высоту BD и среднюю линию KL. Построим прямоугольник, одной стороной которо­го является АС, a другая лежит на прямой KL. Так как пары треугольников АРК и КВТ, а также СLМ и ТВL равны, то треугольник АВС и прямоугольник АРМС равносоставлены.

5. Площадь произвольной плоской фигуры и ее измерение

Мы выяснили, что вычисление площади многоугольника сводится по существу к вычислению площадей треугольников, на которые можно разбить этот многоугольник. А как находить площадь произвольной плоской фигуры? И что представляет собой число, выражающее эту площадь?

Пусть F — произвольная плоская фигура. В геометрии считают, что она имеет площадь S(F), если выполняются следующие условия; существуют многоугольные фигуры, которые содержат F (назовем их объемлющими); существуют многоугольные фигуры, которые содержатся в F (назовем их входящими); площади этих многоугольных фигур как угодно мало отличаются от S(F). Поясним эти положения. На рисунке 7 показано, что фигура Q содержит фигуру Р, т.е. Q, — объемлющая фигура, а фигура Р содержится в F, т.е. Р — входящая фигура. На теоретико-множественном языке это означает, что и, следовательно, можно запи­сать, что .

Если разность площадей объемлющей и входящей фигур может стать как угодно малой, то, как установлено в математике, существует единственное число S(F), удовлетворяющее неравенству для любых многоугольных фигур P и Q. Данное число и считают площадью фигуры F.

Этими теоретическими положениями пользуются, например, когда выводят формулу площади круга. Для этого в круг F радиуса r вписы­вают правильный n-угольник Р, а около окружности описывают правильный n-угольник Q. Если обозначить символами S(Q) и S(P) площади этих многоугольников, то будем иметь, что , причем при возрастании числа сторон вписанных и описанных много­угольников площади S(Р) будут увеличиваться, оставаясь при этом меньше площади круга, а площади S(Q) будут уменьшаться, но оставаться больше площади круга.

Площадь правильного n-угольника равна половине произведения его периметра на радиус вписанной в него окружности. При возрастании числа его сторон периметр стремится к длине окружности , а площадь — к площади круга. Поэтому Sкр = = r 2.

Для приближенного измерения площадей плоских фигур можно использовать различные приборы в частности, палетку.

Палетка — это прозрачная пластина, на которой нанесена сеть квадратов. Сторона квадрата принимается за 1, и чем меньше эта сторона, тем точнее можно измерить площадь фигуры.

Накладываем палетку на данную фигуру F. Квадраты, которые целиком лежат внутри фигуры F, образуют многоугольную фигуру Р; квадраты, имеющие с фигурой F общие точки и целиком лежащие внутри фигуры F, образуют многоугольную фигуру Q (рис. 8). Площади S(Р) и S(Q) находят простым подсчетом квадратов. За приближенное значение площади фигуры F принимается среднее арифметическое найденных площадей:

S(F) = .

В начальном курсе математики учащиеся измеряют площади фигур с помощью палетки таким образом: подсчитывают число квадратов, которые лежат внутри фигуры F, и число квадратов, через которые проходит контур фигуры; затем второе число делят пополам и прибавляют к первому. Полученную сумму считают площадью фигуры F.

Нетрудно обосновать эти действия. Пусть m — число квадратов, которые поместились внутри фигуры F, а n — число квадратов, через которые проходит контур фигуры F. Тогда S(Р) = m, а S(Q) = m + n.

И значит, S(F) = = =

Палетка позволяет измерить площадь фигуры F с определенной точностью. Чтобы получить более точный результат, нужно взять палетку с более мелкими квадратами. Но можно поступить иначе: наложить одну и ту же палетку на фигуру по-разному и найти несколько приближенных значений площади фигуры F. Их среднее арифметическое может быть лучшим приближением к численному значению площади фигуры F.

Лазерная рулетка

Появилась относительно недавно в геодезических бригадах, так как раньше была довольно дорога и сложна в использовании. И по сей день не является единственным прибором для измерения непосредственно расстояний на объекте. Удобно использовать на коротких расстояниях и в помещениях. В уличных условиях применяется не часто, так как необходимо иметь поверхность, на которую можно навести лазерный луч. Также минус многих моделей без оптического визира- плохая видимость лазерной точки на ярко освещенных поверхностях.

Ввиду этого, сейчас все еще достаточно часто приходится использовать стальные рулетки длиной до 50м. Большей длины не выпускают, поэтому расстояния более 50 метров являются источниками ошибок из-за нескольких этапов измерений. Измерения нужно проводить вдвоем, да и провис ленты доставляет некоторую ошибку в измерения.

В итоге лазерные рулетки используются повсеместно кадастровыми инженерами и геодезистами в тех случаях, когда это целесообразно и возможно. Практически все измерения помещений для экспертиз помещений или технических планов без нее не обходятся. В остальных случаях выручает старая-добрая стальная рулетка.

Теодолит

Инструменты, перечисленные в предыдущих пунктах, используются для измерения углов на плоскости. На практике — в геодезии, строительстве, топографии — используется специальный прибор для измерения так называемых горизонтальных и вертикальных углов под названием теодолит. Основными измерительными элементами теодолита являются специальные цилиндрические кольца (лимбы), на которые равномерно нанесена градусная разметка. Установленный с помощью специальной подставки в вершину угла прибор наводится с помощью зрительной трубы сначала на точку, находящуюся на одной стороне угла, где производится замер, затем на другой стороне угла, и снова производится замер. Разность замеров определяет величину угла в первом полуприеме. Затем производится второй полуприем — в обратном направлении. Среднее арифметическое значений, полученных в двух полуприемах является величиной измеряемого угла.

Трубо-кабелеискатель

Прибор, сопутствующий инженерно-геодезическим изысканиям для нанесения подземных коммуникаций на план. Часто в комплект входит генератор, который устанавливается на коммуникацию в ее видимой части. Он генерирует вибрации, которые фиксирует приемник. После обнаружения поворотных точек коммуникации- их наносят на геоподоснову или топографический план. Кабелеискатель также может измерить глубину залегания коммуникации с точностью до 0.01 м.

проверить

Мы рассказали Вам вкратце о геодезических приборах и инструментах, необходимых в прикладной геодезии. Надеемся, что помогли разобраться в тонкостях штативов и «палочек» с которыми работают люди , именующие себя геодезистами.

Ознакомиться со стоимостью наших работ