Механическое преимущество: крутящий момент против скорости вращения
Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.
Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.
Уравнение зубчатой передачи
Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:
Момент входной * Скорость входная = Момент выходной * Скорость выходная
Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.
Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:
0,5 Н∙м * 50 об/с = Момент выходной* 5 об/с.
Ваш выходной крутящий момент будет 5 Н∙м.
Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению
0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость выходная,
Скорость выходная = 5 об/с.
Итак, вы определили, используя простое уравнение, что при показателе Момент выходной =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Конструирование зубчатых и червячных колес
2.4.6.1 Конструкция цилиндрических зубчатых колес
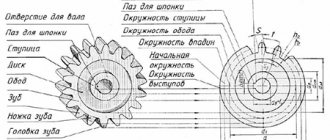
Конструкция зубчатых колес представлена на рис. 2.2. Зубчатые колеса состоят из обода, диска и ступицы.
| а | б |
| Рис. 2.2. Конструкция зубчатого колеса |
Диаметр окружности выступов и ширина зубчатого венца – определяются при проектировочном расчете.
Толщину обода S
для всех типов колес можно принять:
.
На торцах зубчатого венца (зубьях и углах обода) выполняют фаски (рис. 2.3):
,
которые округляют до стандартного значения по тому же ряду, что и (см. табл. 2.3).
На всех прямозубых зубчатых колесах фаску выполняют под углом 45° (рис. 2.3а
). На косозубых и шевронных колесах при твердости менее 350 HB фаску выполняют под углом 45° (рис. 2.3
а
), при более высокой твердости – под углом 15…20° (рис. 2.3
б
).
| а | б |
| Рис. 2.3. Конструкция фаски на торцах зубчатого венца |
Диаметр ступицы наружный (см. рис. 2.2):
– для стальной ступицы при шпоночном соединении и посадке с натягом;
– для стальной ступицы при шлицевом соединении;
– для ступицы из чугуна.
Длина ступицы :
– меньшие значения при посадке на вал с натягом, большие – при переходной посадке;
– оптимальное значение;
Окончательно принимается после расчета соединения вал–ступица.
Зубчатые колеса для редукторов чаще всего имеют симметрично расположенную ступицу.
Острые кромки на торцах ступицы притупляют фасками , размеры которых принимают по таблице 2.5.
Таблица 2.5
Рекомендуемое значение фасок
| 20…30 | 30…40 | 40…50 | 50…80 | 80…120 | 120…150 | 150…250 | 250…500 |
| 1,0 | 1,2 | 1,6 | 2,0 | 2,5 | 3,0 | 4,0 | 5,0 |
Такие же по величине фаски можно применить и для притупления внутренней кромки обода.
Зубчатые колеса небольшого диаметра (до 150 мм) имеют простую форму. Заготовку получают из проката (рис. 2.4а
и рис. 2.5
а
) или свободной ковкой (рис. 2.4
б
и рис. 2.5
б
). Применяются как при серийном, так при единичном производстве.
| а | б |
| Рис. 2.4. Конструкция зубчатых колес небольшого диаметра |
Такую конструкцию можно применять, если толщина обода в месте, ослабленном шпоночным пазом, будет не менее 2,5m
, в противном случае зубчатое колесо надо изготавливать заодно с валом (см. п. 2.4.6.2, «Конструкция вал-шестерней»).
Чтобы уменьшить объем точной обработки резанием на дисках колес выполняют выточки (для колес > 80 мм) (рис. 2.5). Эту же конструкцию колес можно применять для колес большего диаметра (до 500 мм) в единичном производстве, если нет жестких требований к массе.
| а | б |
| Рис. 2.5. Конструкция зубчатых колес небольшого диаметра |
Кованные колеса (рис. 2.6) – колеса большего диаметра (до 500 мм) в единичном и мелкосерийном производстве получают из проката свободной ковкой с последующей токарной обработкой.
| Рис. 2.6. Конструкция кованных зубчатых колес |
Толщина диска . Для уменьшения массы в технически оправданных случаях можно принимать , а в диске выполнить 4…6 отверстий большого диаметра.
Радиусы закруглений .
Штампованные колеса – при серийном производстве заготовки колес диаметром до 500 мм получают из круглого проката ковкой в штампах. При годовом объеме выпуска до 100 шт. экономически оправдана ковка в простейших односторонних подкладных штампах (рис. 2.7). Для свободной выемки заготовок из штампа принимают значения штамповочных уклонов и радиусов закруглений R
³ 6 мм.
| Рис. 2.7. Конструкция штампованных зубчатых колес |
Толщина диска .
При годовом объеме выпуска более 100 шт. применяют двусторонние штампы (рис. 2.8).
| Рис. 2.8. Конструкция штампованных зубчатых колес |
Для уменьшения влияния объемной термообработки на точность геометрической формы зубчатые колеса могут быть сделаны массивными (рис. 2.9): .
| Рис. 2.9. Конструкция штампованных зубчатых колес |
Цельнолитые колеса – применяются в серийном производстве, как наименее трудоемкие, для изготовления колес диаметром свыше 500 мм. По своей несущей способности они уступают колесам с кованным или прокатанным ободом. До диаметра 900 мм их преимущественно выполняют однодисковыми (рис. 2.10а
), а при больших диаметрах и ширине – подкрепляется ребрами (рис. 2.10
б
) или выполняются двухдисковыми (рис. 2.10
в
).
| а | б | в |
| Рис. 2.10. Конструкция литых зубчатых колес |
Спицы могут иметь крестовидное, тавровое, двутавровое, овальное или другой формы сечения. Размеры сечения спиц у ступицы определяются из условного их расчета на изгиб. Поскольку жесткость обода невелика, распределение нагрузки между спицами очень неравномерное. Если окружное усилие на колесе , то условно полагают, что нагрузка, приходящаяся на наиболее нагруженную спицу:
,
где T
– вращающий момент на колесе;
d
– делительный диаметр колеса;
– количество спиц.
Тогда условие прочности спиц:
где – осевой момент сопротивления сечения спицы.
Для свободной выемки заготовок из формы принимают значения литьевых уклонов и радиусов закруглений R
³ 10 мм.
Во избежание биения и вибрации во время работы для зубчатых колес проводят балансировку, высверливая на торце обода отверстия, если их частота вращения превышает 1000 об/мин.
2.4.6.2 Конструкция вал-шестерней
Вал-шестерни применяются в тех случаях, если диаметр вала близок по размерам диаметру шестерни (преимущественно в редукторах при 3,15),
| Рис. 2.11. Конструкция цилиндрических вал-шестерен |
Конструкция вал-шестерни должна обеспечивать нарезание зубьев со свободным выходом инструмента (рис. 2.11а
). При больших передаточных числах допускается изготовление вал-шестерни с врезанием зубьев в тело вала (рис. 2.11
б
,
в
). Выход фрезы определяют графически по ее наружному диаметру. Применения врезных вал-шестерен желательно избегать, так как в этом случае затруднено фрезерование и шлифование зубьев. При этом диаметр окружности впадин шестерни не должен быть меньше расчетного диаметра вала .
По возможности следует предусматривать вход инструмента со стороны заплечика вала (рис. 2.11г
).
2.4.6.3 Конструкция червяков
Червяки выполняют заодно с валом. Насаживаемые червяки применяются крайне редко. Основные размеры червяка (диаметры , , , длина ) определены при проектировании. Ориентировочное расстояние между опорами l
определяется на стадии эскизного проектирования редуктора.
Одним из основных требований, предъявляемых к конструкции вала-червяка, является обеспечение высокой жесткости. С этой целью расстояние между опорами стараются принимать как можно меньше.
| а |
| б |
| в |
| Рис. 2.12. Конструкция цилиндрических червяков |
Диаметр вала-червяка в ненарезанной части выбирают таким, чтобы обеспечить, по возможности, свободный выход инструмента при обработке витков и необходимую величину упорного заплечика для подшипника (рис. 2.12а
).
Если диаметр червяка недостаточно большой для обеспечения нужной высоты заплечика, то необходимо предусмотреть буртик (рис. 2.12б
).
При малом диаметре червяк приходится выполнять по рис. 2.12в
. В этом случае заплечики выполняют как по рис. 2.12
а
, так и по рис. 2.12
б
.
2.4.6.4 Конструкция червячных колес
Основные размеры венца червячного колеса (диаметры , , , , ширина венца ) определены при проектировании.
Радиус выемки поверхности вершин зубьев колеса (рис. 2.13) определяется по диаметру червяка:
,
где – делительный диаметр червяка.
m
– модуль передачи.
| Рис. 2.13. Размеры венца червячного колеса |
На торцах червячного колеса выполняют фаски с округлением до стандартного значения (стандартный размерный ряд фасок дан в табл. 2.6).
Червячные колеса небольшого диаметра (до 100-120 мм) выполняют цельными
. Толщину обода в этом случае можно принять:
.
Размеры диска и ступицы принимают как у сборных колес.
Более крупные колеса изготавливают сборными для экономии дорогостоящих бронз. Диск колеса
выполняют из более дешевых чугунов или сталей,
зубчатый венец
– из бронзы.
Нарезание зубьев червячного колеса выполняют после сборки.
Конструкция диска зависит от объема выпуска. При мелкосерийном производстве заготовки дисков получают из проката или поковок с последующей токарной обработкой (рис. 2.14а
). При серийном производстве (годовой объем выпуска свыше 100 шт.) предпочтительнее изготовление штампованных или литых дисков (рис. 2.14
б
).
Для облегчения выемки заготовки из штампа или литейной формы необходимо на ободе и ступице предусмотреть уклоны и радиусы закругления мм. Для кованных и точеных дисков радиусы закругления принимают мм.
| а | б |
| Рис. 2.14. Конструкция диска сборного червячного колеса |
Толщина червячного венца S
: .
Толщина обода : .
Отсюда наружный диаметр диска: .
Внутренний диаметр обода: .
Толщина диска , но не менее .
Диаметр ступицы наружный :
– для стальной ступицы при шпоночном соединении и посадке с натягом;
– для стальной ступицы при шлицевом соединении;
– для ступицы из чугуна.
Длина ступицы :
– меньшие значения при посадке на вал с натягом, большие – при переходной посадке;
– оптимальное значение;
Окончательно принимается после расчета соединения вал–ступица.
Редукторные червячные колеса чаще всего имеют симметрично расположенную ступицу.
Червячные колеса весом более 20 кг должны иметь 4…6 отверстий на диске для строповки. Диаметр отверстий принимается конструктивно.
Острые кромки на торцах ступицы притупляют фасками , размеры которых принимают по таблице 2.6.
Таблица 2.6
Рекомендуемые размеры фасок f
| 20…30 | 30…40 | 40…50 | 50…80 | 80…120 | 120…150 | 150…250 | 250…500 |
| 1,0 | 1,2 | 1,6 | 2,0 | 2,5 | 3,0 | 4,0 | 5,0 |
Такие же по величине фаски можно применить и для притупления внутренней кромки обода.
Соединение венца с диском должно обеспечивать передачу большого крутящего момента и сравнительно небольшой осевой силы. Конструкция венца и способ соединения с диском зависит от объема выпуска.
При единичном и мелкосерийном производстве
и
небольших размерах колес
( 300 мм) венцы насаживают на диск
с натягом (рис. 2.15).
Толщина обода: .
При постоянном направлении вращения червячного колеса на наружной поверхности диска предусматривают буртик (рис. 2.15а
), который воспринимает осевую силу. Размеры буртика можно принять: ; . Колесо реверсивной передачи можно выполнить без буртика.
| а | б |
| Рис. 2.15. Крепление червячного венца с натягом |
При относительно небольших натягах (или принятии натяга без расчета), для гарантии непроворачиваемости, в стык червячного венца и диска устанавливают винты (рис. 2.15б
) в качестве цилиндрической шпонки (обычно по 3…4 штуки по окружности).
При больших размерах колес
( 300 мм) венец можно прикрепить к диску с помощью призонных болтов (под развертку) (рис. 2.16) или заклепок. В этом случае венец предварительно центрируют по диаметру
D
, сопряжение выполняют по переходной посадке.
Толщина обода: .
| Рис. 2.16. Крепление червячного венца с помощью болтов |
В данной конструкции необходимо предусмотреть надежное стопорение гайки от самоотвинчивания, для этого пружинные шайбы применять не рекомендуется
.
При серийном производстве
экономически выгоднее изготавливать колеса с венцами, получаемыми отливкой. Чугунный или стальной диск нагретый до 700…800ºС закладывают в металлическую форму, подогревают ее до 150…200ºС и заливают расплавленной бронзой. При остывании между диском и венцом возникает натяг, вызываемый усадкой затвердевающего жидкого металла венца.
Толщину венца при отливке принимают .
Диски изготавливают точением, штамповкой или литьем в кокиль. Наружные поверхности литых дисков механически не обрабатывают. Их обезжиривают и очищают от оксидных пленок с помощью химической обработки. На ободе диска предусматривают 6…8 углублений, после отливки на венце образуются выступы, которые воспринимают как окружную, так и осевую силы.
Вогнутую наружную поверхность диска (рис. 2.17а
,
б
) получают точением. Поперечные пазы получают радиальной подачей фрезы: дисковой (рис. 2.17
а
) – перпендикулярно оси вращения колеса или цилиндрической (рис. 2.17
б
) – параллельно оси вращения. Размеры пазов: ; .
Углубления на ободе диска можно высверливать (рис. 2.17в
).
На рис. 2.17г
,
д
показаны диски с пазами, получаемые при литье в диска в кокиль.
| Рис. 2.17. Конструкция червячных венцов, получаемых отливкой |
2.4.6.5 Выбор посадок, предельных отклонений, допусков форм и расположения поверхностей, шероховатостей.
Допуски и предельные отклонения размеров колес и червяков
Допуски на размер диаметра окружности выступов можно принять: для зубчатых колес 7 степени точности – h8
, 8 степени точности –
h9
, 9 степени точности –
h10
. Для 11 степени точности (прямозубые и узкие косозубые колеса передач в ручных приводах) в реверсивных передачах –
h11
, в нереверсивных передачах –
h12
.
Допуск на длину ступицы принимают h11- h12
.
Допуски на остальные размеры обычно принимают по 14 квалитету.
Шероховатость поверхностей колес и червяков
Поверхности элементов зубчатых и червячных передач должны иметь шероховатость, указанные в таблице 2.7.
Таблица 2.7
Шероховатость поверхностей элементов зубчатых и червячных колес
| Элементы зубчатых колес | Шероховатость, Ra, мкм |
| Рабочие поверхности зубьев зубчатых колес | 0,8 – 0,1 |
| Рабочие поверхности зубьев червячных колес | 0,8 – 0,4 |
| Рабочие поверхности витков червяков | 0,4 – 0,2 |
| Поверхности выступов зубьев | 6,3 |
| Фаски и выточки на зубчатых и червячных колесах | 6,3 |
| Торцы ступиц, базирующихся по торцу заплечиков валов, при отношении | 1,6 |
| То же при отношении | 3,2 |
| Рабочие поверхности шпоночных пазов | 1,6 |
| Нерабочие поверхности шпоночных пазов | 3,2 |
| Посадочные поверхности отверстий при посадке H7 : | |
| при диаметрах ≤ 50 мм | 0,8 |
| при диаметрах > 50 мм | 1,6 |
Достижение определенного передаточного числа
Если вы хотите достичь простой его величины, скажем 2 к 1, вы должны использовать две шестерни, одна из которых вдвое больше другой. Это не что иное, как отношение их диаметров. Если диаметр зубчатого колеса в 3 раза больше, чем у сцепленного с ним другого, то вы получите передаточное число 3/1 (или 1/3).
Для гораздо более точного способа вычислить передаточное число подсчитайте отношение зубьев на шестернях. Если одна из них имеет 28 зубьев и другая – 13, вы получите передаточное число 28 / 13 = 2,15 или 13 / 28 = 0,46. Подсчет зубьев всегда будет давать вам наиболее точную величину.
Эффективность передач
К сожалению, в зубчатой передаче вы имеете определенные энергетические потери. Это обусловлено очевидными причинами, такими как трение, рассогласование углов давления, смазкой, зазорами (расстоянием между сцепленными зубьями двух шестерен), а также угловыми моментами и т. д. Различные типы передач, разные виды зубчатых колес, различные материалы и износ шестерен, – все это будет влиять на КПД передачи. Возможные их комбинации дадут слишком большой список, поэтому точную величину КПД передачи, которые вы используете, вы сможете найти в документации на нее.
Предположим, что вы используете два цилиндрических зубчатых колеса. Обычное КПД такой передачи примерно
90%. Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.
Если (из предыдущего примера):
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с,
Истинный Момент выходной = 1 Н∙м * 0,9= 0,9 Н∙м,
Истинная Скорость выходная = 150 об/с * 0,9 = 135 об/с.
Зубчатые цилиндрические колеса
Форму зубчатых колес в большинстве случаев определяют в зависимости от способа получения заготовки. В свою очередь способ получения заготовки выбирают с учетом материала и размеров колес, а также объема выпуска. В единичном и мелкосерийном производстве зубчатые колеса диаметром da ≈ 200 мм изготовляют из круглого проката, поковок и сварные. При da ≈ 150 ÷ 600 мм заготовку получают ковкой в виде круглых поковок. В крупносерийном и массовом производстве заготовки колеса небольших и средних диаметров (da до 600 мм) получают штамповкой в двусторонних штампах, а больших размеров – литьем или сваркой.
Колеса больших диаметров изготовляют обычно литыми, колеса сравнительно тихоходных и малонагруженных передач – литыми и при меньших диаметрах. В индивидуальном производстве колеса больших диаметров выполняют также сварными.
В конструкции зубчатых колес различают (рис. 3) зубчатый венец или обод, ступицу и диск, который соединяет зубчатый венец со ступицей. Зубчатые колеса конструируют двух видов: зубчатый венец выполнен непосредственно на валу (вал-шестерня) и зубчатый венец выполнен совместно с диском и ступицей для соединения с валом при сборке (насадная шестерня).
Рис. 3. Элементы зубчатого колеса
Зубчатый венец шестерни обычно шире на 3…10 мм зубчатого венца колеса. На торцах зубчатого венца выполняют фаски размером f=(0,6…0,7)m. На прямозубых колесах выполняют фаски под углом αφ=45°, на косозубых колесах при твердости рабочих поверхностей НВ<350 выполняют фаски под углом αφ=45°, а при НВ>350 выполняют фаски под углом αφ=15°.
При диаметрах d>500 мм тяжело нагруженные колеса могут выполняться бандажированными. Бандаж (обод) выполняется из легированной стали или бронзы, центр – из дешевой углеродистой стали литым или сварным, а также литым чугунным (рис. 3, в).
Толщина бандажа (мм) по впадинам зубьев: при z<150
при z>150
Ступица. Наружный диаметр ступицы (рис. 4) для стальных колес – dст=(1,55…1,7)d мм и для чугунных – dст=(1,7…1,8)d мм; толщина – δст ≈ (0,3…0,4)d мм; длина – lст=(1,0…1,2)d мм.
Для обеспечения нормальной работы зубчатые и червячные колеса должны быть установлены на валах без перекосов. Если ступица колеса имеет достаточно большую длину lст≥0,8d мм (в редукторах это отношение принято lст=(1…1,5)d мм), то зубчатое или червячное колесо будет сидеть на валу без перекосов.
Рис. 4. Конструкция зубчатого колеса: а – с прямым диском; б – с наклонным диском
В приводах производственных машин и в редукторах применяются зубчатые колеса относительно небольших диаметров, насаживаемые на валы. Их изготовляют из круглого или листового проката, из поковок или сварными. В зависимости от требования конструкции зубчатый венец насадного колеса может располагаться симметрично относительно ступицы или несимметрично. В результате это определяет положение и форму диска, который должен обеспечить устойчивость зубчатого колеса к воспринимаемым нагрузкам.
Для обеспечения прочного сопряжения ступиц зубчатых колес с валами при шпоночном соединении рекомендуют применять следующие посадки (в скобках – для реверсивных передач):
- для цилиндрических прямозубых колес H7/p6 (H7/r6);
- для цилиндрических косозубых и червячных колес H7/r6 (H7/s7);
- для конических колес H7/s7 (H7/t6).
Для обеспечения возможности перемещать колесо на валу в процессе передачи вращения используют посадки H7/g6 (H7/f7).
Диск. Колеса с диаметром вершин зубьев da≤250 мм выполняют в виде дисков, со спицами и без них. У этих стальных колес выполняют углубления на 2…5 мм, чтобы выделить
обрабатываемый торец, который служит технологической базой при нарезании и монтаже колес. Литые зубчатые колеса d ≤500 ÷ 600 мм выполняют (рис. 4) с прямым (а) и наклонным (б) диском.
Рис. 5. Литые зубчатые колеса d ≥500 ÷ 1000 мм: цельное (а); с бандажом (б)
Чугунные колеса, применяемые в тихоходных малонагруженных передачах, наиболее часто открытых, изготовляют литыми. У колес литой конструкции в дисках делают 4…6 отверстий (рис. 5). Отверстия служат для крепления колеса при обработке заготовки и позволяют обрабатывать отверстие под вал и наружную поверхность обода с одной установки, а также используются при транспортировке колес. При больших размерах отверстий они служат для уменьшения массы колес, в литых колесах – для выхода литейных газов при отливке.
Форма спиц для литых колес приведена на рис. 6. Спицы эллиптического сечения применяют при малых нагрузках, крестообразного и таврового сечения – при средних нагрузках, а спицы двухтаврового сечения применяют при работе передачи в тяжелых условиях.
Рис. 6. Формы сечения спиц литых зубчатых колес: а – эллиптическая; б – тавровая; в – крестообразная; г, д – двутавровая
Конструкция кованых зубчатых цилиндрических колес приведена на рис. 7.
Рис. 7. Конструкция кованых зубчатых цилиндрических колес: а – dа≤200 мм; б – dа≤500 мм
Направление вращения шестерен
Разрабатывая любую зубчатую передачу, нужно понимать, как она изменяет направление вращения выходного вала. Две сцепленные шестерни всегда будут вращаться в противоположных направлениях. Это означает, что если одна вращается по часовой стрелке, то другая всегда будет вращаться против нее. Это вполне очевидно. Но что делать, если у вас есть передача, скажем, из шести сцепленных шестерен? Правило здесь следующее: входной и выходной валы у передач с нечетным числом шестерен всегда вращаются в одном направлении, а при четном числе шестерен – в противоположном.
Конструкция и параметры зубчатого колеса
Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.
Читать также: Сколько золота в микросхемах
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
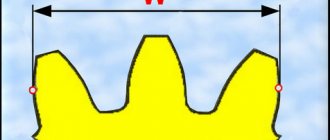
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
Цилиндрические зубчатые колеса (шестерни):
Цилиндрические зубчатые колеса используются в передачах, где оси валов располагаются параллельно относительно друг друга. При этом они могут располагаться как горизонтально, так и вертикально.
В зависимости от формы продольной линии зуба зубчатые колеса бывают: прямозубые, косозубые и шевронные.
Рис. 1. Цилиндрические зубчатые колеса: прямозубые, косозубые и шевронные
Прямозубое колесо. Этот вид шестерен ввиду своей простой конструкции является наиболее внедряемым в различных системах. В таком виде зубья шестерен располагаются в плоскости, которая перпендикулярна оси вращения. В отличии от косозубых и шевронных колес у данного вида предельный крутящий момент ниже.
Косозубое колесо. Зубья для данного вида колес выполняются под определенным углом к оси вращения шестерен, а по форме образуют часть винтовой линии. По сравнению с прямозубым колесом при работе зубьев данного вида зацепление зубьев происходит плавнее, а за счет увеличенной площади контакта предельный крутящий момент выше. Но для работы колес с косым зубом приходится применять упорные подшипники, так как возникает механическая сила, направленная вдоль оси. В основном косозубые колёса используются там, где нужны передачи большого крутящего момента на высоких скоростях.
Шевронное колесо. Этот вид имеет зубья, которые выполнены в форме буквы V на плоскости вращения колеса. Главной особенностью шевронных колес является то, что силы на осях обеих половин компенсируются, вследствие чего отпадает необходимость в использовании упорных подшипников. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов, а также шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.
В отдельные виды выделяются: цилиндрическое колесо с круговыми зубьями, цилиндрическое колесо со смещением (без смещения), циклоидальное, эвольвентное и цевочное цилиндрическое колеса.
Колесо с круговыми зубьями. Передачу с такими колесами называют передачей Новикова. При такой передаче контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс. Зубья данного вида колеса выполнены в виде полукруга, радиус которого подбирается под нужные требования. Колеса с круговыми зубьями в сравнении с косозубыми обладают более высокой нагрузочной способностью зацепления, высокой плавностью и бесшумностью работы, но при тех же условиях работы у них снижен КПД и ресурс работы, что не позволяет их применять широко.
Колесо со смещением либо без смещения. Это зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса.
Циклоидальное колесо. В данном виде профили зубьев шестерни выполнены по циклоидальной кривой. Однако при таком способе зацепления шестерен имеется большой недобор чувствительности из-за изменения расстояния между осями. Циклоидальное колесо применяется в основном в приборостроении. Колесо сложно в изготовлении, поскольку при его создании требуется использование очень многих специальных зуборезных инструментов.
Цевочное колесо. В данном случае зубья одного из колес имеют вид пальцев в форме цилиндра. Такой вид шестерен образовался на базе циклоидального колеса и получил более широкое применение как в машиностроении, так и в приборостроении.
Расчет зубчатого колеса
Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.
Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.
1. Определение передаточного числа u.
2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.
3. Расчет зубьев передачи на изгиб.
4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).
5. Определение межосевого расстояния aW из условия контактной прочности и округление его значения до стандартного.
6. Задание модуля из соотношения m = (0,01 – 0,02) х aW и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.
7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.
8. Выбор коэффициентов формы зубьев для шестерни и колеса.
9. Проверка прочности зубьев по напряжениям изгиба.
10. Проведение геометрического расчета передачи.
11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.
Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.
Зубчатое колесо (шестерня):
Зубчатое колесо или шестерня представляет собой деталь, которая в зависимости от применения может быть с разным количеством зубьев, выполненных в различных формах, располагающихся на цилиндрической или конической поверхности, и которая входит в зацепление с зубьями другого зубчатого колеса.
Зубчатые колеса или шестерни, за счет сцепления зубьев, выполняют следующие задачи: передача вращательного движения от одной детали к другой с изменением крутящего момента, увеличением или уменьшением скорости, а также преобразование вращательного движения в поступательное с помощью зубчатой рейки.
Зубчатые передачи широко применяются как в машиностроении, так и в приборостроении.
Зубчатые колеса подразделяются на виды в зависимости от применения и бывают цилиндрическими и коническими.
Как обозначается точность изготовления зубчатых колес
При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:
- кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
- погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
- погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
- боковой зазор между неработающими поверхностями зубьев.
Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:
- вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
- допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.
Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.
Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:
8-Ас ГОСТ 1643 – 81.
Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:
5-4-3-Са ГОСТ 1643 – 81.
Конические зубчатые колёса
Прямозубые конические колёса применяют при невысоких окружных скоростях (до 2…3 м/с, допустимо до 8 м/с). При более высоких скоростях целесообразно применять колёса с круговыми зубьями, как обеспечивающие более плавное зацепление, меньший шум, большую несущую способность и более технологичные. Прямозубые конические передачи обеспечивают передаточное отношение до 3.
| При окружных скоростях, больших 3 м/с, в конических редукторах применяют зубчатые передачи с косыми или криволинейными зубьями, которые благодаря постепенному входу в зацепление и меньшим изменением величины деформации зубьев в процессе зацепления работают с меньшим шумом и меньшими динамическими нагрузками. Кроме того, зубчатые колёса с косыми или криволинейными зубьями лучше работают на изгиб, чем прямозубые. Однако для полного контакта зубьев этих передач требуется прилегание зубьев не только по их ширине, но и по высоте, что повышает требования к изготовлению косозубых передач и колёс с криволинейными зубьями. Благодаря своим преимуществам такие передачи могут применяться при передаточных отношениях до 5 и даже выше. | Рисунок 5 а) с прямыми зубьями, б) с косыми зубьями, в) с криволинейными зубьями, г) коническая гипоидная передача |
Рисунок 6 — Основные элементы зубьев конических колёс | Конические зубчатые колёса с косыми зубьями могут работать с окружной скоростью до 12 м/с, а колёса с криволинейными зубьями — до 35-40 м/с. Наибольшее распространение получили передачи с криволинейными зубьями, нарезанными по спирали, эвольвенте (паллоидные) или окружности (круговые).Конические колёса с криволинейными зубьями могут иметь различное направление спирали. Зубчатое колесо называется правоспиральным, если со стороны вершины конуса зубья наклонены наружу в сторону движения часовой стрелки, в противном случае колесо называется левоспиральным. |
Корригирование конических зубчатых колёс
Применяют в основном высотную коррекцию (корригирование) конических колёс. Также для конических колёс применяется тангенциальная коррекция, заключающаяся в утолщении зуба шестерни и утонении зуба колеса. Тангенциальная коррекция конических колёс не требует специального инструмента. Для цилиндрических колёс тангенциальную коррекцию не применяют, так как для она требует специального инструмента. На практике для конических колёс часто применяют высотную коррекцию в сочетании с тангенциальной.
Зубья конических колёс по признаку изменения размеров сечений по длине выполняют трех форм:
| Рисунок 7 | 1.Нормально понижающие зубья. Вершины делительного и внутреннего конусов совпадают. Эту форму применяют для конических передач с прямыми и тангенциальными зубьями, а также ограниченно для передач с круговыми зубьями при mn>2 и Z = 20…100. | Рисунок 8 | 2. Вершина внутреннего конуса располагается так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу растёт с увеличением расстояния до вершины. Эта форма позволяет обрабатывать одним инструментом сразу обе поверхности зубьев колеса. Поэтому она является основой для колес с круговыми зубьями. | Рисунок 9 | 3. Равновысокие зубья. Образующие делительного и внутреннего конуса параллельны. Эту форму применяют для круговых зубьев при Z>40, в частности при средних конусных расстояниях 75-750 мм. |
Типы зубчатых передач
Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.
Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.
Цилиндрические прямозубые колеса (КПД
Цилиндрическое зубчатое колесо имеет зубья, расположенные на цилиндрической поверхности. Передачи с ними являются наиболее часто используемыми типами благодаря своей простоте и максимальной эффективности среди всех других. Передаточное число для одной пары u ≤ 12,5. Не рекомендуется для очень высоких нагрузок, так как прямые зубья зубчатого колеса довольно легко ломаются.
Виды зубчатых колес и область применения
Цилиндрические зубчатые колеса прямозубые.
С наружным и внутренним зацеплением. Служат для передачи энергии вращения между валами с параллельными осями. Наиболее распространены благодаря сравнительной простоте изготовления, обслуживания, надежности и малым габаритам. Применяются во всех отраслях машиностроения: станкостроение, тяжелое оборудование, автомобильное производство, производство редукторов и др. Передачи с прямозубыми цилиндрическими колесами обладают наиболее высокой кинематической точностью. Поэтому востребованы в приборостроении.
Конические зубчатые колеса
(с прямой и тангенциальной формой зуба). Для зубчатых передач с пересекающимися осями (обычно под 90 градусов). Требуют для изготовления специальных станков, более требовательны к точности изготовления, точности установки, усложняют конструкцию опор валов.
Применяются во фрезерных и зубонарезных станках. Также нашли применение в конических редукторах, дифференциальных механизмах — там, где по компоновке редуктора предусмотрены передачи с пересекающимися осями.
Червячные колеса.
Для зубчатых передач с перекрещивающимися (обычно под 90 градусов) осями. Сложнее цилиндрических колес в изготовлении, быстрее изнашиваются.
Обладают низким уровнем шума, плавностью хода, обусловленные особенностями механического зацепления червяка и червячного колеса. Эти свойства ценятся в металлообрабатывающих станках, цеховых электрокарах, мешалках, бетономешалках, приводах ворот и т.д.
Только у червячных колес есть эффект «самоторможения» для передач с передаточным числом свыше 1:35. При остановке электродвигателя выходной вал невозможно провернуть. Поэтому червячные колеса применяют в редукторах там, где важна техника безопасности, сохранность грузов при перегрузке: подъемники, наклонные транспортеры. При определённых требованиях это позволяет сэкономить на дополнительном тормозном устройстве.
Цилиндрические косозубые колеса (КПД
Они работают так же, как цилиндрические прямозубые, для передачи момента между параллельными валами, но у такой передачи более плавно происходит зацепление. Вследствие этого они создают меньше шума при работе и имеют меньшие габариты. У них большая нагрузочная способность. К сожалению, из-за сложной формы зубьев они, как правило, более дорогие.
Червячные передачи (КПД
Это передача с винтом-червяком на одном валу и червячным колесом на втором, перпендикулярном первому, валу. Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).
Для выполнения расчетов, чертежей и эскизов зубчатых колёс и других деталей зубчатых передач надо знать основные элементы и параметры зубчатых зацеплений и условности, принятые для изображения зубчатого венца.
Рис. 17. Шестерни с элементами фиксации на валу
Основным элементом зубчатого колеса является зуб.
Начальная поверхность делит зуб по его высоте на две неравные части – головку и ножку. Часть зуба, расположенная над делительной поверхностью, называется головкой зуба, а расположенная ниже делительной поверхности – ножкой зуба. Зубья с ободом составляют венец зубчатого колеса, который через диск или спицы соединён со ступицей, имеющей отверстие для вала, зачастую с элементами фиксации колеса на валу, например, при помощи шпоночного (рис. 17,
а
) или шлицевого (рис. 17,
б)
соединений.
Читать также: Как сделать патрон для мини дрели
Стальные зубчатые колеса
Зубчатые колеса диаметром до 150 мм в единичном и мелкосерийном производстве обычно изготовляют из круглого проката; в средне-, крупносерийном и массовом производстве предпочтительнее применять кованые или штампованные заготовки, имеющие более высокие механические характеристики.
Шестерни изготовляют за одно целое с валом (вал-шестерня) (рис. 1, а, б) или делают съемными, если расстояние χ от впадины зуба до шпоночного паза (рис. 2) больше 2,5 mn для цилиндрических шестерен и 1,8 me для конических. В случае цельной конструкции увеличивается жесткость вала и уменьшается общая стоимость вала и шестерни. Разъемная конструкция позволяет выполнить шестерню и вал из разных материалов, а при поломке одной детали вторую оставить без замены. На рис. 1, а показана конструкция вала-шестерни, когда диаметр впадин зубьев df1 превышает диаметр вала dб.п. (диаметр буртика подшипника), что обеспечивает свободный выход инструмента при нарезании зубьев. При df1 < dб.п. (рис. 1, б) выход фрезы lвых определяют прочерчиванием по ее наружному диаметру Dф, который принимают по табл. 1 в зависимости от mn и степени точности передачи.
Цилиндрические зубчатые колеса диаметром до 400… 500 мм (в отдельных случаях до 600 мм) можно выполнять коваными, штампованными, литыми или сварными.
Конструктивные элементы зубчатых колес показаны на рис. 3.
Типовые конструкции зубчатых колес и основные соотношения их элементов даны на рис. 4—8. Кованые заготовки для зубчатых колес применяют при наружном диаметре колеса 4,df < 200 мм или при нешироких колесах (ψba < 0,2) диаметром da до 400 мм. Операция штамповки отличается высокой производительностью и максимально приближает форму заготовки к форме готового колеса. Для облегчения заполнения металлом и освобождения от заготовки штамп, а следовательно, и заготовка должны иметь радиусы закруглений r ≥ 5 мм и штамповочные уклоны γ ≥ 5° (рис. 4). Внутреннюю поверхность обода, наружную поверхность ступицы и поверхности диска штампованных колес обычно не обрабатывают. Конструкция литого колеса дана на рис. 5.
Таблица 1. Значения диаметра фрезы Dф, мм
| Степень прочности передачи | Номинальный модуль mn, мм | |||||
| 2…2,25 | 2,25…2,75 | 3…3,75 | 4…4,5 | 5…5,5 | 6…7 | |
| 7 8…10 | 90 70 | 100 80 | 112 90 | 125 100 | 140 112 | 160 125 |
Рис. 1. Конструкция вала — шестерни Рис. 2. Элемент шестерни при шпоночном соединении Рис. 3. Конструктивные элементы колес: a — цилиндрического; б — конического; в — червячного Рис. 4. Цилиндрические зубчатые колеса при da≤ 500мм: а —штампованное; б— кованое; dст= 1,6dв; lст≥ bпри соблюдении условия lст= (0,8…1,5)dв; δ o= 2,5mn+2 , но не менее 8…10 мм; n = 0,5mn для обода, n для ступицы в зависимости от диаметра dв; Dотв= 0,5(Do+dст); dотв= 15…25 мм; c = (0,2…0,3)b для штампованных и c = (0,2…0,3)b для кованых колес Рис. 5. Литое цилиндрическое зубчатое колесо при da= 400…1000 мм: b ≤ 200 мм dст= 1,6dв — для стального литья; dст= 1,8dв для чугунного литья; lст≥ b при соблюдении условия lст= (0,8…1,5)dв; δ o= 2,5mn+ 2 ≥ 8 мм; n = 0,5mn для обода n для ступицы; c = H/5, но не менее 10 мм; S = H/5, но не менее 10 мм; e = 0,8δ o; H= 0,8dв; H1= 0,8H; R — вписанная дуга окружности Рис. 6. Бандажированное зубчатое колесо при dв свыше 600 мм: dст= 1,6dв — для стального литья; dст= 1,8dв — для чугунного;lст≥ b при соблюдении условия lст= (0,8…1,5)dв; c = 0,15b; δ o= 4mn, но не менее 15 мм; t = δ o; e = 0,8δ o; d1= (0,05…0,1)dв; l1= 3d1;b ≥ 300 мм Рис. 7. Сварное зубчатое колесо: lст= (0,8…1,5)dв≥ b; dст= 1,6dв; δ o= 2,5mn, но не менее 8 мм;s = 0,8c ; Dотв= 0,5 (Do+ dст); dотв= 15…20 мм. Катеты швов: Ka= 0,5dв; Kь= 0,1dв но не менее 4 мм. Ребра приваривают швом Kб Рис. 8. Шевронное зубчатое колесо с канавкой посередине: lст= b + a; c = (0,3…0,35)(b + a); δ o= 4mn+ 2; h = 2,5mn; a — в зависимости от модуля. Остальные размеры см. рис. 4, 5
Размеры ступицы выбирают по рекомендациям, приведенным под рисунками. Длину ступицы lст по возможности принимают равной ширине венца колеса b, что обеспечивает наименьшую ширину редуктора. Отношение длины ступицы к диаметру вала должно быть не меньше 0,5. При отношении меньше 0,8 на валу предусматривают буртик, исключающий торцевое биение колеса, к которому будет прижиматься торец ступицы колеса. Если по условиям расчета (см. расчет шпоночного и шлицевого соединений) lст> b, то ступицу желательно сместить по оси колеса до совпадения одного ее торца с торцом венца (см. рис. 3, а), что дает возможность нарезать зубья сразу на двух колесах. Реже (для одноступенчатых редукторов) колеса изготовляют со ступицей, выступающей в обе стороны относительно венца (рис. 3, в), при этом зубья можно нарезать только на одном колесе. При одинаковой длине ступицы и ширине венца можно одновременно нарезать зубья на нескольких колесах.
С целью экономии материала, при больших диаметрах колес, для соединения ступицы с венцом колеса вместо сплошного диска применяют спицы. Зубчатые колеса большого диаметра (при внешнем диаметре da≥ 600 мм) иногда делают бандажированными (рис. 6): венец — стальной кованый (бандаж), а колесный центр — из стального или чугунного литья. Венец сопрягается с колесным центром посадкой с гарантированным натягом. Для большей надежности в плоскости соединения венца с центром ставят винты; соединения проверяют на смятие по материалу колесного центра: при стальном колесном центре [σ] см≥ 0,3σ т, при чугунном [σ] см≥ 0,4σ в.и, где σ т — предел текучести; σ в.и — предел прочности чугуна на изгиб.
При индивидуальном изготовлении колёса иногда делают сварными (рис. 7). При диаметре da≥ 1500 мм для удобства сборки зубчатые колеса делают разъемными — из двух половин.
На торцах зубьев и обода выполняют фаски n = 0,5mn, размер которых округляют до стандартного значения 1; 1,2; 1,6; 2; 2,5; 3; 4; 5.
Острые кромки на торцах ступицы притупляют фасками n x 45, размер которых принимают в зависимости от диаметра вала d:
| d, мм n, мм | 20…30 1 | 30…40 1,2 | 40…50 1,6 | 50…80 2 |
| Продолжение | ||||
| d, мм n, мм | 80…120 2,5 | 120…150 3 | 150…250 4 | 250…500 5 |
Шевронные зубчатые колеса (рис.  отличаются от других цилиндрических колес большей шириной. Наиболее часто шевронные колеса изготовляют с канавкой посередине, предназначенной для выхода червячной фрезы, нарезающей зубья. При известных размерах фрезы ширину канавки a определяют прочерчиванием. Приближенно размер а можно определить в зависимости от модуля m:
отличаются от других цилиндрических колес большей шириной. Наиболее часто шевронные колеса изготовляют с канавкой посередине, предназначенной для выхода червячной фрезы, нарезающей зубья. При известных размерах фрезы ширину канавки a определяют прочерчиванием. Приближенно размер а можно определить в зависимости от модуля m:
| m, мм a, мм | 1,5 27 | 2 32 | 2,5 37 | 3 42 | 3,5 47 | 4 53 | 5 60 | 6 67 | 7 75 | 8 85 | 10 100 |
Остальные конструктивные элементы шевронных колес принимают по соотношениям, указанным под рис. 8.
Конические зубчатые колеса изготовляют коваными, штампованными, литыми или из круглого проката (рис. 9—11).
Конические колеса с внешним диаметром вершин зубьев dae< 120 мм конструируют, как показано на рис. 9. В том случае, когда угол делительного конуса σ < 30 °, колесо выполняют по рис. 9, а, при σ < 45 ° — по рис. 9, б. Если 30° ≤ σ ≤ 45° , можно использовать обе формы. Штампованные колеса (рис. 10, а) применяют в серийном производстве. При внешнем диаметре вершин dae≥ 300 мм используют также литые конические колеса с ребрами жесткости.
Ступицу в зубчатых конических колесах необходимо располагать так, чтобы при закреплении колеса на оправке для нарезания зубьев обеспечивался зазор а> 0,5 mte для свободного выхода инструмента, где т,е внешний окружной модуль (рис. 11).
Рис. 9. Конические зубчатые колеса при dae< 120 мм: a — при δ < 30° ; б— при 5 >45°; диаметр ступицы dст= 1,6dв; lст= (0,9…1,2)dв; δ o= 2,5mn+ 2, но не менее 10 мм; n = 0,5mn Рис. 10. Конические зубчатые колеса при dae до 500 мм: а — штампованное; б — кованое dст= 1,6dв; lст= (0,9…1,2)dв., но не менее 10 мм; c = (0,1…0,17)Re; n = 0,5mn; размеры Dотв и dотв определяют конструктивно Рис. 11. Крепление конического колеса при нарезании зубьев Рис. 12. Зубчатое колесо из пластмассы со стальной втулкой (ступицей), установленной при формовании колес Рис. 13.13. Зубчатое колесо (шестерня) из пластмассы со стальной сборной ступицей
В дисках цилиндрических и конических зубчатых колес предусматривают отверстия диаметром dотв, используемые для закрепления при обработке на станках и при транспортировке. При больших размерах отверстий они служат для уменьшения массы колес, а в литых колесах также для выхода литейных газов при отливке.