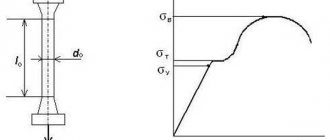
Расчёты на прочность при изгибе
Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом. Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта
Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.
Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.
Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:
- дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
- способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
- семейство принятых гипотез;
- разработанные правила построения графических изображений (построение эпюр).
Расчёт параметров производится в три этапа:
- при проверочном расчёте (вычисляют величину максимального напряжения);
- на этапе проектирования (производится выбор толщины и параметров сечения бруса);
- во время вычисления допустимой нагрузки.
Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.
Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:
- на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
- на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
- в точке появления приложенного момента, скачок равен величине этого параметра;
- на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
- в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).
На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:
- расчёт производят с учётом нормальных напряжений;
- в качестве основного предположения принимают гипотезу о плоских сечениях;
- продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
- деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
- для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
- физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
- процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).
Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.
Закон Гука
Наблюдения за различными видами деформации показали, что величина деформации тела зависит от механического напряжения, возникающего под действием приложенных к телу сил.
Эту зависимость описывает закон, открытый в 1660 г. английским учёным Робертом Гуком, которого называют одним из отцов экспериментальной физики.
Виды деформации удобно рассматривать на модели бруса. Это тело, один из трёх размеров которого (ширина, высота или длина), гораздо больше двух других. Иногда вместо термина «брус» употребляют термин «стержень». У стержня длина намного превышает его ширину и высоту.
Рассмотрим эту зависимость для деформации растяжения-сжатия.
Предположим, что стержень первоначально имеет длину L. Под действием внешних сил его длина изменится на величину ∆l. Она называется абсолютным удлинением (сжатием) стержня.
Для деформации растяжения-сжатия закон Гука имеет вид:
F – сила, сжимающая или растягивающая стержень; k – коэффициент упругости.
Сила упругости прямо пропорциональна удлинению тела до некого предельного значения.
Е – модуль упругости первого рода или модуль Юнга. Его величина зависит от свойств материала. Это теоретическая величина, введённая для характеристики упругих свойств тел.
S
– площадь поперечного сечения стержня.
Отношение абсолютного удлинения к первоначальной длине стержня называют относительным удлинением или относительной деформацией.
При растяжении его величина имеет положительное значение, а при сжатии отрицательное.
Отношение модуля внешней силы к площади поперечного сечения стержня называется механическим напряжением.
Тогда закон Гука для относительных величин будет выглядеть так:
Напряжение σ прямо пропорционально относительной деформации ε.
Считается, что сила, стремящаяся удлинить стержень, является положительной (F ˃ 0), а сила, укорачивающая его, имеет отрицательное значение (F ˂ 0).
Дальнейшее чтение [ править ]
- Базант, Зденек П .; Седолин, Луиджи (2010). Неустойчивости трехмерного континуума и эффекты тензора конечных деформаций, глава 11 в «Устойчивости структур», 3-е изд . Сингапур, Нью-Джерси, Лондон: World Scientific Publishing. ISBN 9814317039.
- Дилл, Эллис Гарольд (2006). Механика сплошной среды: упругость, пластичность, вязкоупругость . Германия: CRC Press. ISBN 0-8493-9779-0.
- Хаттер, Колумбан; Йёнк, Клаус (2004). Континуальные методы физического моделирования . Германия: Springer. ISBN 3-540-20619-1.
- Jirasek, M; Базант, ЗП (2002). Неупругий анализ конструкций . Лондон и Нью-Йорк: J. Wiley & Sons. ISBN 0471987166.
- Любарда, Владо А. (2001). Теория упругопластичности . CRC Press. ISBN 0-8493-1138-1.
- Макоско, CW (1994). Реология: принципы, измерения и приложения
. Издатели ВЧ. ISBN 1-56081-579-5. - Мейс, Джордж Э. (1970). Механика сплошной среды . McGraw-Hill Professional. ISBN 0-07-040663-4.
- Мейс, Дж. Томас; Мейс, Джордж Э. (1999). Механика сплошной среды для инженеров (2-е изд.). CRC Press. ISBN 0-8493-1855-6.
- Немат-Насер, Сиа (2006). Пластичность: трактат о конечной деформации неоднородных неупругих материалов . Кембридж: Издательство Кембриджского университета. ISBN 0-521-83979-3.
- Прагер, Уильям (1961). Введение в механику сплошных сред . Бостон: ISBN Ginn and Co. 0486438090.
| Авторитетный контроль |
|
Основные понятия
Под кручением понимают вид деформации, свойственный для условий приложения к телу силы в поперечной плоскости. В результате этого в поперечном разрезе формируется крутящий момент. Деформациям кручения подвергаются валы и пружины.
Валом называют функционирующую на кручение вращающуюся деталь в виде стержня.
Под торсионом понимают функционирующий на кручение стержень, применяемый в качестве упругого элемента.
Для круглых валов, наиболее обширно применяемых в технике, разработана теория кручения. Она основана на трех положениях:
- После деформации сохраняется плоское поперечное сечение детали.
- При деформации радиусы, проходящие поперек детали, не искривляются и проворачиваются на равный угол.
- При деформации продольные волокна сохраняют размеры, следовательно, разделяющие поперечные сечения расстояния неизменны.
Из приведенных положений следует, что кручение представлено деформацией сдвига материала между соседними поперечными сечениями, обусловленной проворотом последних вокруг оси.
Деформациями при кручении считают взаимный проворот сечений. Они формируются вследствие воздействия на стержень пар сил с перпендикулярными к его продольной оси плоскостями действия.
Угол закручивания стержня цилиндрической конфигурации в границах упругих деформаций определяется уравнением закона Гука для кручения, представляющего отношение произведения момента и длины вала к произведению геометрического полярного инерционного момента и модуля сдвига.
Относительный угол закручивания вычисляют как частное угла закручивания и длины стержня.
Под вращающими либо скручивающими моментами понимают показатели пар сил, воздействующих на вал. Их подразделяют на внешние, называемые вращающими и скручивающими, и внутренние (крутящие). Под влиянием перпендикулярных продольной оси бруса внешних крутящих моментов формируются внутренние. Они передаются на деталь в точках установки шкивов ременных передач, зубчатых колес и т. д.
Крутящий момент представлен силовым фактором, обуславливающим круговое передвижение сечения относительно перпендикулярной ему оси или препятствующим ему. Его значение равно сумме скручивающих усилий по одну сторону от данной точки. Положительными считают внутренние моменты, направленные против часовой стрелки со стороны внешней нормали (отброшенной части). При этом соответствующий внешний момент имеет направление, совпадающее с ходом часовой стрелки.
Условия прочности и жесткости применяют для решения следующих задач:
- Выполнения проверочного расчета данных условий для конкретных значений крутящего момента и валов определенного размера и материала.
- Выполнения проектировочного расчета для вычисления диаметров и нахождения большего из них.
- Определения грузоподъемности вала путем вычисления крутящего момента из обоих условий и нахождения меньшего из них.
Под эпюрой крутящих моментов понимают график, отображающий закон их изменения по длине либо сечению детали.
При разделении детали по длине на три участка в соответствии с методом сечений получится, что для первого (правого) фрагмента наблюдается линейная зависимость крутящего момента от координаты сечения ввиду влияния равномерно распределенной нагрузки, для второго и третьего участков данная зависимость отсутствует. При этом в точках приложения внешних сосредоточенных усилий наблюдаются скачки, соответствующие их величине.
В сечении наблюдается линейное изменение, определяемое законом касательных напряжений, в прямой зависимости от расстояния от центра.
Полярный инерционный момент сечения представляет собой геометрическую характеристику жесткости при кручении для круглого вала. Полярный момент сопротивления сечения является аналогичным параметром для его прочности.
Следует отметить, что большинство приведенных выше понятий описывается с применением формул.
Кручение
Если виды механических деформаций разделяли бы по сложности вычислений, то этот занял бы первое место. Такой вид изменения формы тела возникает при воздействии на него двух сил. При этом смещение любой точки тела происходит перпендикулярно к оси воздействующих сил. Говоря о таком типе деформации, следует упомянуть следующие величины, подлежащие вычислению:
- Ф — угол закручивания цилиндрического стержня.
- Т — момент действия.
- Л — длина стержня.
- Г — момент инерции.
- Ж — модуль сдвига.
Формула выглядит так:
Ф=(Т*Л)/(Г*Ж).
Другая величина, требующая вычисления, это относительный угол закручивания:
Q=Ф/Л (значения берутся из предыдущей формулы).
Закон Гука
Наблюдения за различными видами деформации показали, что величина деформации тела зависит от механического напряжения, возникающего под действием приложенных к телу сил.
Эту зависимость описывает закон, открытый в 1660 г. английским учёным Робертом Гуком, которого называют одним из отцов экспериментальной физики.
Виды деформации удобно рассматривать на модели бруса. Это тело, один из трёх размеров которого (ширина, высота или длина), гораздо больше двух других. Иногда вместо термина «брус» употребляют термин «стержень». У стержня длина намного превышает его ширину и высоту.
Рассмотрим эту зависимость для деформации растяжения-сжатия.
Предположим, что стержень первоначально имеет длину L. Под действием внешних сил его длина изменится на величину ∆l. Она называется абсолютным удлинением (сжатием) стержня.
Для деформации растяжения-сжатия закон Гука имеет вид:
F — сила, сжимающая или растягивающая стержень; k — коэффициент упругости.
Сила упругости прямо пропорциональна удлинению тела до некого предельного значения.
Е — модуль упругости первого рода или модуль Юнга. Его величина зависит от свойств материала. Это теоретическая величина, введённая для характеристики упругих свойств тел.
S
— площадь поперечного сечения стержня.
Отношение абсолютного удлинения к первоначальной длине стержня называют относительным удлинением или относительной деформацией.
При растяжении его величина имеет положительное значение, а при сжатии отрицательное.
Отношение модуля внешней силы к площади поперечного сечения стержня называется механическим напряжением.
Тогда закон Гука для относительных величин будет выглядеть так:
Напряжение σ прямо пропорционально относительной деформации ε.
Считается, что сила, стремящаяся удлинить стержень, является положительной (F ˃ 0), а сила, укорачивающая его, имеет отрицательное значение (F ˂ 0).
Определение и общие сведения о деформации сдвига
Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.
Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:
- при распиловке бруса;
- отрезание или рубка металла;
- в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
- балки в местах крепления опор;
- места скрепления мостовых пролётов;
- крепёж на перемычках соединения железнодорожных рельс;
- разрезания листа бумаги ножницами.
При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.
Для оценки величины сдвига и надёжности конструкции используют следующие параметры:
- величина, направление и точка приложения воздействующей силы;
- модуль сдвига;
- угол изменения внешних граней изделия;
- тангенциальное напряжение;
- модуль кручения (зависит от физико-механических характеристик материала);
Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.
В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.
Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.
В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:
- оптические (в том числе лазерные);
- акустические;
- рентгеновские; электрические;
- пневматические.
В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.
Описание деформации [ править ]
Деформация — это изменение метрических свойств непрерывного тела, означающее, что кривая, нарисованная при первоначальном размещении тела, изменяет свою длину при смещении до кривой при окончательном размещении. Если ни одна из кривых не меняет длину, говорят, что произошло смещение твердого тела .
Удобно определить эталонную конфигурацию или начальное геометрическое состояние континуального тела, из которого будут ссылаться все последующие конфигурации. Эталонная конфигурация не обязательно должна быть той, которую тело действительно когда-либо займет. Часто конфигурация при t
= 0 считается эталонной конфигурацией
κ
0 (
B
) . Конфигурация в текущий момент t — это
текущая конфигурация
.
Для анализа деформации эталонная конфигурация определяется как недеформированная конфигурация
, а текущая конфигурация — как
деформированная конфигурация
. Кроме того, время не учитывается при анализе деформации, поэтому последовательность конфигураций между недеформированной и деформированной конфигурациями не представляет интереса.
Компоненты X
i
вектора положения
X
частицы в эталонной конфигурации, взятые относительно эталонной системы координат, называются
материальными или эталонными координатами
. С другой стороны, компоненты
xi
вектора положения
x
частицы в деформированной конфигурации, взятые относительно пространственной системы координат отсчета, называются
пространственными координатами
Есть два метода анализа деформации сплошной среды. Одно описание сделано в терминах материальных или ссылочных координат, и оно называется описанием материала или лагранжевым описанием . Второе описание деформации производится в терминах пространственных координат, оно называется пространственным описанием или эйлеровым описанием .
При деформации сплошного тела существует непрерывность в том смысле, что:
- Материальные точки, образующие замкнутую кривую в любой момент, всегда будут образовывать замкнутую кривую в любое последующее время.
- Материальные точки, образующие замкнутую поверхность в любой момент, всегда будут образовывать замкнутую поверхность в любое последующее время, и материя внутри замкнутой поверхности всегда будет оставаться внутри.
Аффинная деформация [ править ]
Деформация называется аффинной деформацией, если ее можно описать аффинным преобразованием . Такое преобразование состоит из линейного преобразования (такого как вращение, сдвиг, растяжение и сжатие) и перемещения твердого тела. Аффинные деформации также называют однородными деформациями. [8]
Следовательно, аффинная деформация имеет вид
x ( X , t ) = F ( t ) ⋅ X + c ( t ) {\displaystyle \mathbf {x} (\mathbf {X} ,t)={\boldsymbol {F}}(t)\cdot \mathbf {X} +\mathbf {c} (t)}
где x
— положение точки в деформированной конфигурации,
X
— положение в эталонной конфигурации, t — параметр времени,
F
— линейный преобразователь, а
c
— перенос. В матричной форме, где компоненты относятся к ортонормированному базису,
[ x 1 ( X 1 , X 2 , X 3 , t ) x 2 ( X 1 , X 2 , X 3 , t ) x 3 ( X 1 , X 2 , X 3 , t ) ] = [ F 11 ( t ) F 12 ( t ) F 13 ( t ) F 21 ( t ) F 22 ( t ) F 23 ( t ) F 31 ( t ) F 32 ( t ) F 33 ( t ) ] [ X 1 X 2 X 3 ] + [ c 1 ( t ) c 2 ( t ) c 3 ( t ) ] {\displaystyle {\begin{bmatrix}x_{1}(X_{1},X_{2},X_{3},t)\\x_{2}(X_{1},X_{2},X_{3},t)\\x_{3}(X_{1},X_{2},X_{3},t)\end{bmatrix}}={\begin{bmatrix}F_{11}(t)&F_{12}(t)&F_{13}(t)\\F_{21}(t)&F_{22}(t)&F_{23}(t)\\F_{31}(t)&F_{32}(t)&F_{33}(t)\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\end{bmatrix}}+{\begin{bmatrix}c_{1}(t)\\c_{2}(t)\\c_{3}(t)\end{bmatrix}}}
Вышеупомянутая деформация становится неаффинной
или
неоднородной,
если
F
=
F
(
X
,
t
) или
c
=
c
(
X
,
t
) .
Движение твердого тела [ править ]
Движение твердого тела — это особая аффинная деформация, которая не включает сдвиг, растяжение или сжатие. Матрица преобразования F
является собственной ортогональной , чтобы позволить ротацию , но никаких отражений .
Движение твердого тела можно описать следующим образом:
x ( X , t ) = Q ( t ) ⋅ X + c ( t ) {\displaystyle \mathbf {x} (\mathbf {X} ,t)={\boldsymbol {Q}}(t)\cdot \mathbf {X} +\mathbf {c} (t)}
где
Q ⋅ Q T = Q T ⋅ Q = 1 {\displaystyle {\boldsymbol {Q}}\cdot {\boldsymbol {Q}}^{T}={\boldsymbol {Q}}^{T}\cdot {\boldsymbol {Q}}={\boldsymbol {\mathit {1}}}}
В матричной форме
[ x 1 ( X 1 , X 2 , X 3 , t ) x 2 ( X 1 , X 2 , X 3 , t ) x 3 ( X 1 , X 2 , X 3 , t ) ] = [ Q 11 ( t ) Q 12 ( t ) Q 13 ( t ) Q 21 ( t ) Q 22 ( t ) Q 23 ( t ) Q 31 ( t ) Q 32 ( t ) Q 33 ( t ) ] [ X 1 X 2 X 3 ] + [ c 1 ( t ) c 2 ( t ) c 3 ( t ) ] {\displaystyle {\begin{bmatrix}x_{1}(X_{1},X_{2},X_{3},t)\\x_{2}(X_{1},X_{2},X_{3},t)\\x_{3}(X_{1},X_{2},X_{3},t)\end{bmatrix}}={\begin{bmatrix}Q_{11}(t)&Q_{12}(t)&Q_{13}(t)\\Q_{21}(t)&Q_{22}(t)&Q_{23}(t)\\Q_{31}(t)&Q_{32}(t)&Q_{33}(t)\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\end{bmatrix}}+{\begin{bmatrix}c_{1}(t)\\c_{2}(t)\\c_{3}(t)\end{bmatrix}}}
Прочность и деформации
Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство — прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.
Напряжение при сдвиге
Воздействие внешней силы на грань приводит к возникновению в изделии изменения формы. Все напряжения делятся на две категории: нормальные и касательные. Нормальными считаются внутренние напряжения, возникающие в различных слоях изделия, подверженного деформации.
Напряжения и деформации при сдвиге описываются с применением аналитических выражений и графических изображений. Общее состояние описывается пространственным (трёхкоординатным) напряжением. Если в конкретном случае можно выявить сечения, в которых оба вида напряжений равны нулю, можно перейти к более простым моделям описания этого процесса. Ими являются двухкоординатное (плоское) напряжённое состояние или линейное. Две последних модели являются частными случаями трёхкоординатного напряжённого состояния.
Классификация
В общем случае можно выделить следующие виды деформации: упругие и неупругие. Упругие, или обратимые, деформации исчезают после того, как пропадает воздействующая на них сила. Основа этого физического закона используется в силовых тренажёрах, например, в эспандере. Если говорить о физической составляющей, то в основе лежит обратимое смещение атомов — они не выходят за пределы взаимодействия и рамки межатомных связей.
Неупругие (необратимые) деформации, как вы понимаете, являются противоположным процессом. Любая сила, которую приложили к телу, оставляет следы/деформацию. К этому типу воздействия относится и деформация металлов. При таком типе изменения формы зачастую могут меняться и другие свойства материала. Например, при деформации, вызванной охлаждением, может увеличиться прочность изделия.
Типы деформации
В зависимости от того, как приложена внешняя сила, различают деформации растяжения-сжатия, сдвига, изгиба, кручения.
Деформация растяжения-сжатия
Деформация растяжения-сжатия вызывается силами, которые приложены к концам бруса параллельно его продольной оси и направлены в разные стороны.
Под действием внешних сил частицы твёрдого вещества, колеблющиеся относительно своего положения равновесия, смещаются. Но этому процессу пытаются помешать внутренние силы взаимодействия между частицами, старающиеся удержать их в исходном положении на определённом расстоянии друг от друга. Силы, препятствующие деформации, называются силами упругости.
Деформацию растяжения испытывают натянутая тетива лука, буксировочный трос автомобиля при буксировке, сцепные устройства железнодорожных вагонов и др.
Когда мы поднимается по лестнице, ступеньки под действием нашей силы тяжести деформируются. Это деформация сжатия. Такую же деформацию испытывают фундаменты зданий, колонны, стены, шест, с которым прыгает спортсмен.
Деформация сдвига
Если приложить внешнюю силу по касательной к поверхности бруска, нижняя часть которого закреплена, то возникает деформация сдвига. В этом случае параллельные слои тела как бы сдвигаются относительно друг друга.
Представим себе расшатанный табурет, стоящий на полу. Приложим к нему силу по касательной к его поверхности, то есть, попросту потянем верхнюю часть табурета на себя. Все его плоскости, параллельные полу, сместятся друг относительно друга на одинаковый угол.
Такая же деформация происходит, когда лист бумаги разрезается ножницами, пилой с острыми зубьями распиливается деревянный брус и др. Деформации сдвига подвергаются все крепёжные детали, соединяющие поверхности, – винты, гайки и др.
Деформация изгиба
Такая деформация возникает, если концы бруса или стержня лежат на двух опорах. В этом случае на него действуют нагрузки, перпендикулярные его продольной оси.
Деформацию изгиба испытывают все горизонтальные поверхности, положенные на вертикальные опоры. Самый простой пример – линейка, лежащая на двух книгах одинаковой толщины. Когда мы поставим на неё сверху что-то тяжёлое, она прогнётся. Точно так же прогибается деревянный мостик, перекинутый через ручей, когда мы идём по нему.
Деформация кручения
Кручение возникает в теле, если приложить пару сил к его поперечному сечению. В этом случае поперечные сечения будут поворачиваться вокруг оси тела и относительно друг друга. Такую деформацию наблюдают у вращающихся валов машин. Если вручную отжимать (выкручивать) мокрое бельё, то оно также будет подвергаться деформации кручения.
Смещение [ править ]
Рис. 1. Движение сплошного тела.
Изменение конфигурации сплошного тела приводит к смещению . Смещение тела состоит из двух компонентов: смещения твердого тела и деформации. Смещение твердого тела состоит из одновременного перемещения и вращения тела без изменения его формы или размера. Деформация подразумевает изменение формы и / или размера тела от исходной или недеформированной конфигурации κ
0 (
B
) до текущей или деформированной конфигурации
κ t
(
B
) (Рисунок 1).
Если после смещения континуума происходит относительное смещение между частицами, произошла деформация. С другой стороны, если после смещения континуума относительное смещение между частицами в текущей конфигурации равно нулю, то деформации нет, и говорят, что произошло смещение твердого тела.
Вектор, соединяющий положения частицы P
в недеформированной конфигурации и деформированной конфигурации, называется вектором смещения
u
(
X
,
t
) =
uiei
в лагранжевом описании, или
U
(
x
,
t
) =
UJEJ
в эйлерово описание.
Поле смещения
представляет собой векторное поле всех векторов смещения для всех частиц в теле, которое связывает деформированную конфигурацию с недеформированной конфигурацией. Анализ деформации или движения сплошного тела удобно проводить в терминах поля смещения. В общем, поле смещения выражается через материальные координаты как
u ( X , t ) = b ( X , t ) + x ( X , t ) − X or u i = α i J b J + x i − α i J X J {\displaystyle \ \mathbf {u} (\mathbf {X} ,t)=\mathbf {b} (\mathbf {X} ,t)+\mathbf {x} (\mathbf {X} ,t)-\mathbf {X} \qquad {\text{or}}\qquad u_{i}=\alpha _{iJ}b_{J}+x_{i}-\alpha _{iJ}X_{J}}
или в терминах пространственных координат как
U ( x , t ) = b ( x , t ) + x − X ( x , t ) or U J = b J + α J i x i − X J {\displaystyle \ \mathbf {U} (\mathbf {x} ,t)=\mathbf {b} (\mathbf {x} ,t)+\mathbf {x} -\mathbf {X} (\mathbf {x} ,t)\qquad {\text{or}}\qquad U_{J}=b_{J}+\alpha _{Ji}x_{i}-X_{J}\,}
где α Ji
— направляющие косинусы между материальной и пространственной системами координат с единичными векторами
EJ
и
ei
, соответственно. Таким образом
E J ⋅ e i = α J i = α i J {\displaystyle \ \mathbf {E} _{J}\cdot \mathbf {e} _{i}=\alpha _{Ji}=\alpha _{iJ}}
и соотношение между u i
и
U J
определяется выражением
u i = α i J U J or U J = α J i u i {\displaystyle \ u_{i}=\alpha _{iJ}U_{J}\qquad {\text{or}}\qquad U_{J}=\alpha _{Ji}u_{i}}
Знаю это
e i = α i J E J {\displaystyle \ \mathbf {e} _{i}=\alpha _{iJ}\mathbf {E} _{J}}
тогда
u ( X , t ) = u i e i = u i ( α i J E J ) = U J E J = U ( x , t ) {\displaystyle \mathbf {u} (\mathbf {X} ,t)=u_{i}\mathbf {e} _{i}=u_{i}(\alpha _{iJ}\mathbf {E} _{J})=U_{J}\mathbf {E} _{J}=\mathbf {U} (\mathbf {x} ,t)}
Обычно системы координат для недеформированной и деформированной конфигураций накладываются друг на друга, что приводит к b
= 0 , а направляющие косинусы становятся дельтами Кронекера :
E J ⋅ e i = δ J i = δ i J {\displaystyle \ \mathbf {E} _{J}\cdot \mathbf {e} _{i}=\delta _{Ji}=\delta _{iJ}}
Таким образом, мы имеем
u ( X , t ) = x ( X , t ) − X or u i = x i − δ i J X J = x i − X i {\displaystyle \ \mathbf {u} (\mathbf {X} ,t)=\mathbf {x} (\mathbf {X} ,t)-\mathbf {X} \qquad {\text{or}}\qquad u_{i}=x_{i}-\delta _{iJ}X_{J}=x_{i}-X_{i}}
или в терминах пространственных координат как
U ( x , t ) = x − X ( x , t ) or U J = δ J i x i − X J = x J − X J {\displaystyle \ \mathbf {U} (\mathbf {x} ,t)=\mathbf {x} -\mathbf {X} (\mathbf {x} ,t)\qquad {\text{or}}\qquad U_{J}=\delta _{Ji}x_{i}-X_{J}=x_{J}-X_{J}}
Тензор градиента смещения [ править ]
Частичное дифференцирование вектора смещения по координатам материала дает тензор градиента смещения материала
∇ X u
. Таким образом, мы имеем:
| u ( X , t ) = x ( X , t ) − X ∇ X u = ∇ X x − I ∇ X u = F − I {\displaystyle {\begin{aligned}\mathbf {u} (\mathbf {X} ,t)&=\mathbf {x} (\mathbf {X} ,t)-\mathbf {X} \\\nabla _{\mathbf {X} }\mathbf {u} &=\nabla _{\mathbf {X} }\mathbf {x} -\mathbf {I} \\\nabla _{\mathbf {X} }\mathbf {u} &=\mathbf {F} -\mathbf {I} \\\end{aligned}}} | или же | u i = x i − δ i J X J = x i − X i ∂ u i ∂ X K = ∂ x i ∂ X K − δ i K {\displaystyle {\begin{aligned}u_{i}&=x_{i}-\delta _{iJ}X_{J}=x_{i}-X_{i}\\{\frac {\partial u_{i}}{\partial X_{K}}}&={\frac {\partial x_{i}}{\partial X_{K}}}-\delta _{iK}\\\end{aligned}}} |
где F
—
тензор градиента деформации
.
Аналогичным образом , частичная дифференциация вектора смещения по отношению к пространственным координатам дает пространственное перемещение тензора градиента
∇ х U
. Таким образом, мы имеем
| U ( x , t ) = x − X ( x , t ) ∇ x U = I − ∇ x X ∇ x U = I − F − 1 {\displaystyle {\begin{aligned}\mathbf {U} (\mathbf {x} ,t)&=\mathbf {x} -\mathbf {X} (\mathbf {x} ,t)\\\nabla _{\mathbf {x} }\mathbf {U} &=\mathbf {I} -\nabla _{\mathbf {x} }\mathbf {X} \\\nabla _{\mathbf {x} }\mathbf {U} &=\mathbf {I} -\mathbf {F} ^{-1}\\\end{aligned}}} | или же | U J = δ J i x i − X J = x J − X J ∂ U J ∂ x k = δ J k − ∂ X J ∂ x k {\displaystyle {\begin{aligned}U_{J}&=\delta _{Ji}x_{i}-X_{J}=x_{J}-X_{J}\\{\frac {\partial U_{J}}{\partial x_{k}}}&=\delta _{Jk}-{\frac {\partial X_{J}}{\partial x_{k}}}\\\end{aligned}}} |
Сжатие и растяжение
Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.
Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.
СОДЕРЖАНИЕ
- 1 штамм 1.1 Меры деформации 1.1.1 Инженерная нагрузка
- 1.1.2 Коэффициент растяжения
- 1.1.3 Истинное напряжение
- 1.1.4 Зеленый штамм
- 1.1.5 Штамм Альманси
- 1.2.1 Нормальная деформация
- 2.1 Аффинная деформация
- 3.1 Тензор градиента смещения
- 4.1 Плоская деформация 4.1.1 Деформация изохорной плоскости
Деформации на примере организма человека
Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:
- Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
- Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
- Изгиб характерен для конечностей, костей таза, позвонков.
- Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.
Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.
По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.
Прочность и деформации
Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство — прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.
Закон Гука
Математические расчеты, необходимые в строительстве, технике, позволили применять закон Гука для деформации сдвига. Формула показывала прямую связь между силой, прикладываемой к телу, и его удлинением (сжатием). Гук использовал коэффициент жесткости, показывая связь между материалом и возможностью его деформации.
По мере развития и совершенствования технических средств, аппаратов и приборов, разработки теории сопротивления, были проведены серьезные исследования пластичности и упругости. Результаты проведенных фундаментальных экспериментов стали применять в строительной технике, теории сооружений, теоретической механике.
Благодаря комплексному подходу к проблемам, связанным с различными видами деформации, удалось развить строительную отрасль, осуществлять профилактику правильной осанки у подрастающего поколения страны.
Ссылки [ править ]
- Truesdell, C .; Нолл, В. (2004). Нелинейные полевые теории механики
(3-е изд.). Springer. п. 48. - Ву, Х.-К. (2005). Механика сплошной среды и пластичность
. CRC Press. ISBN 1-58488-363-4. - Lubliner, Jacob (2008). Теория пластичности (PDF) (Пересмотренная ред.). Dover Publications. ISBN 0-486-46290-0. Архивировано из оригинального (PDF) 31 марта 2010 года.
- ^ a b Рис, Дэвид (2006). Базовая инженерная пластичность: введение в инженерные и производственные приложения . Баттерворт-Хайнеманн. ISBN 0-7506-8025-3. Архивировано 22 декабря 2017 года.
- ↑
«Земля». Британская энциклопедия из DVD Encyclopdia Britannica 2006 Ultimate Reference Suite [2009]. - Рис, Дэвид (2006). Базовая инженерная пластичность: введение в инженерные и производственные приложения . Баттерворт-Хайнеманн. п. 41. ISBN 0-7506-8025-3. Архивировано 22 декабря 2022 года.
- Хенки, Х. (1928). «Улучшенная форма эластичности эластичных элементов идеального эластичного материала». Zeitschrift für technische Physik
.
9
: 215–220. - ^ a b c Огден, RW (1984). Нелинейные упругие деформации
. Дувр.