Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Электромагнитная природа сил упругости
По физической природе силы упругости ближе к силам трения, чем к силам гравитации, так как они вызваны взаимодействием заряженных частиц, которые являются основой всех тел.
Однако силы упругости определяют только взаимное расположение воздействующих друг на друга тел и появляются только при деформации, тогда как силы трения скольжения возникают при относительном движении тел.
На расстояниях около диаметра молекулы силы притяжения между молекулами компенсированы силами отталкивания, то есть равнодействующая сил притяжения и отталкивания равна нулю. Если тело растягивать, то расстояние между молекулами увеличивается, при этом силы притяжения между молекулами становятся больше по величине, чем силы отталкивания. В теле появляются силы, которые препятствуют растяжению тела. При сжимании тела расстояние между молекулами уменьшается. Силы отталкивания становятся по модулю больше, чем силы притяжения, так возникают силы, противостоящие такого рода деформации тела.
Так, при деформации тел появляются силы электромагнитной природы, которые препятствуют изменению размеров тела, это так называемые силы упругости.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Деформация тела
Определение
Деформацией тела называют изменение размеров или формы тела. Виды деформаций: растяжение, сжатие, сдвиг, изгиб, кручение. Деформации тела возникают при перемещении одних частей тела по отношению к другим.
Силы упругости возникают только при деформациях. Величина силы упругости зависит от размера деформации. Силы упругости направлены против направления смещения частей тела при его деформации.
Для твердых тел выделяют два предельных вида деформации: упругие деформации и пластические. Если после прекращения действия деформирующей силы тело полностью восстанавливает свои размеры и форму, то такой вид деформации называют упругой. Для упругих деформаций существует однозначная зависимость между величиной деформации и деформирующей силой. Если после снятия деформирующей силы тело не восстанавливает (или восстанавливает не полностью) свои размер и форму, то такие деформации называют пластическими.
Определение силы упругости
Определение Силой упругости (${\overline{F}}_{upr}$) называют силу, которая действует со стороны тела подвергшегося деформации, на касающиеся его тела. Данная сила направлена в сторону, противоположную смещению частей тела в состоянии деформации.
Силы упругости зависят от расположения тел при их взаимодействии и возникают только при деформациях тел.
Силы упругости направлены перпендикулярно к поверхности соприкосновения взаимодействующих тел. Исключение составляет деформация сдвига, при такой деформации сила упругости имеет касательную составляющую.
Силы упругости играют важную роль в проблемах механического равновесия, в том случае, если модели недеформируемого тела не достаточно.
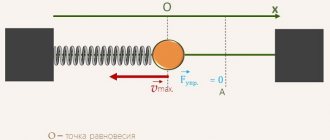
Силы упругости являются частой причиной возникновения механических колебаний. При упругой деформации появляются силы, которые стремятся вернуть тело в положение равновесия. Если тело вывели из состояния равновесия и предоставили самому себе, то под воздействием си упругости появляется движение этого тела к положению равновесия. В результате существования инерции тело проходит положение равновесия и тогда возникает деформация противоположного знака, при этом процесс повторяется.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Закон Гука
Эксперименты показывают, что почти у всех твердых тел при небольших упругих деформациях размер деформации пропорционален деформирующей силе. Эта зависимость была установлена английским ученым Р. Гуком. Закон упругой деформации носит имя своего первооткрывателя. При больших деформациях связь между величиной деформации и деформирующей силой становится неоднозначной и точно нелинейной, упругая деформация превращается в пластическую.
Закон Гука утверждает, что при малых упругих деформациях величина деформации пропорциональна силе ее вызывающей. Закон Гука справедлив при видах упругой деформации (растяжения, сжатия, сдвига, кручения, изгиба).
Например, деформацию растяжения (сжатия) характеризуют с помощью такой величины как абсолютное удлинение: ($\Delta l=\left|l-l_0\right|$, где $l_0$ — длина недеформированного стержня). Тогда закон Гука для силы упругости записывают как:
\[F_{upr}=k\Delta l\ \left(1\right).\]
где $k$ — коэффициент упругости , $\left[k\right]=\frac{Н}{м}$. Коэффициент упругости зависит от материала тела, его размеров и формы.
Закон Гука выполняется с хорошей точностью для деформаций, появляющихся в стержнях из стали, чугуна, и других твердых веществ, в пружинах.
Для всяких упругих деформаций можно ввести постоянные, которые характеризуют упругие свойства только материала и не зависят от размеров тела. Например, модуль Юнга ($E$) для изотропного тела является характеристикой упругих свойств. Модуль Юнга равен механическому напряжению ($\sigma =\frac{F}{S},\ где\ F-\ $деформирующая сила или сила, возникающая в теле при деформации; $S$ — площадь), при котором относительное удлинение ($\frac{\Delta l}{l_0}$) равно единице при упругой деформации:
\[\frac{\Delta l}{l_0}=\frac{1}{E}\sigma \left(2\right).\]
Значение модуля Юнга определяют эмпирически.
Если деформации тела малы, то силы упругости можно определять по ускорению, которое данные силы сообщают телам. Если тело неподвижно, то модуль силы упругости находят из равенства нулю векторной суммы сил, которые действуют на тело.
Так, будет деформация упругой или пластической зависит не только от материала тела, но и от величины приложенной нагрузки. Упругие деформации много применяют, например, в амортизационных устройствах: рессорах, пружинах и т.д. На основе пластической деформации базируется разные виды холодной обработки металлов: прокатка, ковка и т.д.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Имеются две абсолютно упругие пружины. Под действием одной и той же силы первая пружина удлинилась на 8 см, а вторая — на 4 см. Сравните жёсткость \( k_2 \) второй пружины с жёсткостью \( k_1 \) первой пружины.
1) \( k_1=k_2 \) 2) \( 4k_1=k_2 \) 3) \( 2k_1=k_2 \) 4) \( k_1=2k_2 \)
2. Имеются две абсолютно упругие пружины: одна жёсткостью 200 Н/м, другая жёсткостью 400 Н/м. Сравните силу упругости \( F_2 \), возникающую во второй пружине, с силой упругости \( F_1 \), возникающей в первой пружине, при одинаковом их удлинении.
1) \( F_2=F_1 \) 2) \( F_2=4F_1 \) 3) \( 2F_2=F_1 \) 4) \( 0.5F_2=F_1 \)
3. Ученик, растягивая пружину динамометра последовательно на 1Н, 2Н, ЗН и 4Н, каждый раз измерял её удлинение и результаты измерений вносил в таблицу. Определите по данным таблицы жёсткость пружины динамометра.
1) 0,02 Н/м 2) 0,5 Н/м 3) 2 Н/м 4) 50 Н/м
4. На рисунке приведены графики зависимости силы упругости от удлинения. Сравните жёсткость пружин.
1) \( k_2=k_1 \) 2) \( k_2>k_1 \) 3) \( k_2 4) \( k_2\geq k_1 \)
5. Учащийся выполнял эксперимент по измерению удлинения \( x \) пружин при подвешивании к ним грузов. Полученные учащимся результаты представлены на рисунке в виде диаграммы. Какой вывод о жёсткости пружин \( k_1 \) и \( k_2 \) можно сделать из анализа диаграммы, если к концам пружин были подвешены грузы одинаковой массы?
1) \( k_2=4k_1 \) 2) \( k_1=2k_2 \) 3) \( k_2=2k_1 \) 4) \( k_1=k_2 \)
6. Под действием силы 3 Н пружина удлинилась на 4 см. Чему равна сила, под действием которой удлинение этой пружины составит 6 см?
1) 3,5 Н 2) 4 Н 3) 4,5 Н 4) 5 Н
7. Две пружины растягиваются одинаковыми силами. Жёсткость первой пружины \( k_1 \) в 2 раза больше жесткости второй пружины \( k_2 \). Удлинение первой пружины \( \Delta l_1 \), удлинение второй пружины \( \Delta l_2 \) равно
1) \( 0.5\Delta l_1 \) 2) \( 0.67\Delta l_1 \) 3) \( 1.5\Delta l_1 \) 4) \( 2.5\Delta l_1 \)
8. В лифте, движущемся вниз равноускоренно из состояния покоя, стоит ящик. Модуль веса ящика
1) равен модулю силы тяжести 2) больше модуля силы тяжести 3) меньше модуля силы тяжести 4) увеличивается с увеличением скорости лифта
9. Человек испытывает перегрузки при
1) равномерном движении вниз 2) равномерном движении вверх 3) равноускоренном движении вверх из состояния покоя 4) равноускоренном движении вниз с ускорением свободного падения
10. Различие веса тела на экваторе и на полюсе можно обнаружить
А. Взвешивая тело на рычажных весах Б. Взвешивая тело на пружинных весах
Правильный ответ
1)только А 2)только Б 3) и А, и Б 4) ни А, ни Б
11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА A. Модуль силы упругости пружины Б. Жёсткость пружины B. Модуль удлинения пружины
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ 1) уменьшается 2) увеличивается 3) не изменяется
12. Из приведённых ниже высказываний выберите два верных и запишите их номера в таблицу.
1) Закон Гука справедлив при любых деформациях. 2) Сила упругости направлена в сторону, противоположную деформации. 3) Жёсткость зависит только от материала, из которого изготовлено тело. 4) Вес тела всегда равен действующей на него силе тяжести. 5) Вес приложен к опоре или к подвесу.
Часть 2
13. Груз массой 5 кг начинают поднимать вертикально вверх с ускорением 2 м/с2. Чему равен вес груза?