14Ноя
- By: Семантика
- Без рубрики
- Comment: 0
При строительстве объектов обязательно необходимо использовать расчеты, включающие подробные характеристики стройматериалов. В обратном случае на опору может быть возложена слишком большая, непосильная нагрузка, из-за чего произойдет разрушения. Сегодня поговорим о пределе прочности материала при разрыве и натяжении, расскажем, что это такое и как работать с этим показанием.
Предел прочности
ПП – будем использовать это сокращение, а также можно говорить об официальном сочетании «временное сопротивление» – это максимальная механическая сила, которая может быть применена к объекту до начала его разрушения. В данном случае мы не говорим о химическом воздействии, но подразумеваем, что нагревание, неблагоприятные климатические условия, определенная среда могут либо улучшать свойства металла (а также дерева, пластмассы), либо ухудшать.
Ни один инженер не использует при проектировании крайние значения, потому что необходимо оставить допустимую погрешность – на окружающие факторы, на длительность эксплуатации. Рассказали, что называется пределом прочности, теперь перейдем к особенностям определения.
Как производится испытание на прочность
Изначально особенных мероприятий не было. Люди брали предмет, использовали его, а как только он ломался, анализировали поломку и снижали нагрузку на аналогичное изделие. Теперь процедура гораздо сложнее, однако, до настоящего времени самый объективный способ узнать ПП – эмпирический путь, то есть опыты и эксперименты.
Все испытания проходят в специальных условиях с большим количеством точной техники, которая фиксирует состояние, характеристики подопытного материала. Обычно он закреплен и испытывает различные воздействия – растяжение, сжатие. Их оказывают инструменты с высокой точностью – отмечается каждая тысячная ньютона из прикладываемой силы. Одновременно с этим фиксируется каждая деформация, когда она происходит. Еще один метод не лабораторный, а вычислительный. Но обычно математический анализ используется вместе с испытаниями.
Определение термина
Образец растягивается на испытательной машине. При этом сначала он удлиняется в размере, а поперечное сечение становится уже, а затем образуется шейка – место, где самый тонкий диаметр, именно здесь заготовка разорвется. Это актуально для вязких сплавов, в то время как хрупкие, к ним относится чугун и твердая сталь, растягиваются совсем незначительно без образования шейки. Подробнее посмотрим на видео:
Диаграмма растяжения низкоуглеродистой стали
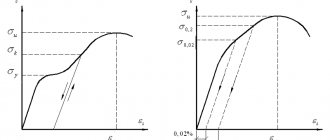
На рис. 3.2 изображена диаграмма растяжения низкоуглеродистой стали (ст.3), записанная с помощью специального устройства на испытательной машине.
В начальной стадии нагружения до некоторой точки А диаграмма растяжения представляет собой наклонную прямую, что указывает на пропорциональность между нагрузкой и деформацией – справедливость закона Гука. Нагрузка, при которой эта пропорциональность еще не нарушается, на диаграмме обозначена через Pпц
и используется для вычисления предела пропорциональности:
, (3.1)
где F
– площадь поперечного сечения образца до испытания.
Пределом пропорциональности называется наибольшее напряжение, до которого существует прямо пропорциональная зависимость между нагрузкой, и деформацией. Для ст.3 предел пропорциональности приблизительно равен МПа.
Зона ОА называется зоной упругости. Здесь возникают только упругие, очень незначительные деформации. Данные, характеризующие эту зону, позволяют определить значение модуля упругости Е
.
После достижения предела пропорциональности деформация начинает расти быстрее, чем нагрузка, я диаграмма становится криволинейной. На этом участке в непосредственной близости от точки А находится точка В, соответствующая пределу упругости.
Пределом упругости называется максимальное напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации.
Предел упругости существует независимо от закона прямой пропорциональности. Он характеризует начало перехода от упругой деформации к пластической.
У большинства металлов значения предела пропорциональности и предела упругости незначительно отличаются друг, от друга. Поэтому обычно считают, что они практически совпадают. Для стали ст.3 МПа.
При дальнейшем нагружении криволинейная часть диаграммы переходит в почти горизонтальный участок CD – площадку текучести. Здесь деформации растут практически без увеличения нагрузки. Нагрузка Рт
, соответствующая точке D, используется при определении физического предела текучести:
(3.2)
Физическим пределом текучести называется наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки.
Предел текучести является одной из основных механических характеристик прочности металлов. Для стали ст.3 МПа.
Зона BD называется зоной общей текучести. В этой зоне значительно развиваются пластические деформации. При этом у образца повышается температура, изменяются электропроводность и магнитные свойства.
Диаграмма после зоны текучести снова становится криволинейной. Образец приобретает способность воспринимать возрастающее усилие до значения Рmax
– точка
E
на диаграмме. Усилие
Рmax
используется для вычисления временного сопротивления:
. (3.3)
Напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца, называется временным сопротивлением.
Для стали марки ст.3 временное сопротивление МПа.
Зона DE называется зоной упрочнения. Здесь удлинение образца происходит равномерно по всей его длине, первоначальная цилиндрическая форма образца сохраняется, а поперечные сечения изменяются незначительно и также равномерно.
При максимальном усилии или несколько меньшем его на образце в наиболее слабом месте возникает локальное уменьшение поперечного сечения – шейка (а иногда и две). Дальнейшая деформация происходит в этой зове образца. Сечение в середине шейки продолжает быстро уменьшаться, но напряжения в этом сечении все время растут, хотя растягивающее усилие и убывает. Вне области шейки напряжения уменьшаются, и поэтому удлинение остальной, части образца не происходит. Наконец, в точке К образец разрушается. Сила, соответствующая точке К, называется разрушающей Рк
, а напряжения –
истинным сопротивлением разрыву (истинным пределом прочности), которые равны:
, (3.4)
где Fк
– площадь поперечного сечения в месте разрыва.
Зона ЕК называется зоной местной текучести, Истинные напряжения в момент разрыва (в шейке) в образце из стали ст.3 достигают 900. 1000 МПа.
Интересен механизм разрушения образца из низкоуглеродистой стали. Образец разрушается, как правило, с образованием «чашечки» на одной его части и «конуса» – на другой. Этот излом называют чашечным или изломом «чашечка – конус».
Помимо указанных характеристик прочности, после разрушения образца определяют характеристики пластичности.
Относительное удлинение после разрыва (%) – это отношение приращения расчетной длины образца после разрыва к ее первоначальному значению, вычисляемое по формуле:
Предел прочности на растяжение стали
Стальные конструкции давно заменили прочие материалы, так как они обладают отличными эксплуатационными характеристиками – долговечностью, надежностью и безопасностью. В зависимости от применяемой технологии, он подразделяется на марки. От самой обычной с ПП в 300 Мпа, до наиболее твердой с высоким содержанием углерода – 900 Мпа. Это зависит от двух показателей:
- Какие способы термообработки применялись – отжиг, закалка, криообработка.
- Какие примеси содержатся в составе. Одни считаются вредными, от них избавляются для чистоты сплава, а вторые добавляют для укрепления.
Свойства, определяемые испытанием на растяжение, и факторы, на них влияющие
Предел прочности
Пределом прочности называют максимальное усилие растяжения, отнесенное к единице площади его первоначального сечения
σВ=P/F
,
Па
Другими словами, предел прочности есть условное максимальное напряжение, которое выдерживает материал при растяжении. Под «истинным пределом прочности»(или под действительным сопротивлением разрыву) понимается усилие в момент разрыва P
, отнесенное к площади сечения.
Предел пропорциональности и упругости
Под пределом пропорциональности σПЦ
понимают наименьшее напряжение вызывающее в испытуемом материале отклонение от закона пропорциональности (или наибольшее напряжение от этого закона), а под пределом упругости
σУП
— наибольшее напряжение, ниже которого величина деформации является определенной функцией напряжения, независимо от возрастания или убывания последнего, то нет оснований предполагать идентичность этих двух величин.
Предел текучести
Пределом текучести σТ
называется напряжение, при котором возникающая остаточная деформация образца распространяется равномерно по его рабочей части при временном постоянстве растягивающего усилия.
Практически в качестве предела текучести обычно принимается напряжение, при котором деформация образца возрастает, а стрелка динамометра разрывной машины либо останавливается, либо отходит назад. В этом случае на кривой «напряжение — деформация» образуется так называемая площадка текучести (кривая a
), и тогда предел текучести называют явным или физическим.
Типичные кривые растяжения (α — ε)
В некоторых случаях площадка текучести бывает неясно выражена (кривая б
) или совершенно отсутствует (кривая
в
); такую форму кривых при нормальной температуре испытания имеют весьма пластичные металлы (например, медь). С повышением же температуре явным пределом текучести, форма кривой имеет вид, показанный на рисунке,
в
. Мягкая углеродистая сталь с содержанием 0,05% при 300°С дает кривую, соответствующую кривой
б
; другие, более теплоустойчивые стали сохраняют явный предел текучести до 400 и даже до 500°С; выше этих температур форма кривых растяжения аналогична кривой
в
.
Во всех случаях, когда отсутствует явный предел текучести, приходится прибегать к нахождению так называемых условных пределов текучести, основанных на определении напряжений, вызывающих заданную остаточную деформацию небольшой величины (в пределах 0,01—0,5%). Чаще всего на практике определяют условные пределы текучести, вызывающие остаточную деформацию, равную 0,1 или 0,2%.
Условные пределы текучести некоторых легированных сталей
Если условные пределы текучести при нормальной температуре мало различаются между собой, то при высоких температурах разница между условными пределами текучести, например 0,01 и 0,2% (после текучести), становится значительной.
Удлинение и поперечное сужение образца
Удлинение и поперечное сужение образца, испытанного при высокой температуре, являются показателями пластических свойств металла при данной температуре.
Удлинение δ
и поперечное сужение
ψ
замеряются на охлажденных образцах и подсчитываются по общеизвестным формулам:
- где l0
— начальная длина расчетного участка образца; - lk
— конечная длина расчетного участка образца; - F0
— начальная площадь поперечного сечения образца; - Fk
— конечная площадь поперечного сечения образца.
Наибольшее влияние на эти свойства оказывает время до разрыва или, что то же самое, скорость растяжения образца.
Модуль упругости
Модуль нормальной упругости E
является важной физико-механической характеристикой металла. Знание величины модуля упругости стали для широкого диапазона температур необходимо не только при конструкторских расчетах деталей машин и аппаратуры, работающих при повышенных температурах, но и в ряде других случаев.
Относительное изменение модуля упругости E (в % от его значения при 20°) в зависимости от температуры для сталей: 1-нелегированной; 2-низколегированной; 3-среднелегированной; 4-высоколегированной
Усталость стали
Второе название – предел выносливости. Его обозначают буквой R. Это аналогичный показатель, то есть он определяет, какая сила может воздействовать на элемент, но не в единичном случае, а в цикле. То есть на подопытный эталон циклично, раз за разом действуют определенные давления. Среднее количество повторений – 10 в седьмой степени. Именно столько раз металл должен без деформаций и потери своих характеристик выдержать воздействие.
Если проводить эмпирические испытания, то потребуется множество времени – нужно проверить все значения силы, прикладывая ее по множеству циклов. Поэтому обычно коэффициент рассчитывается математически.
Предел пропорциональности
Это показатель, определяющий длительность оказываемых нагрузок к деформации тела. При этом оба значения должны изменяться в разный степени по закону Гука. Простыми словами: чем больше оказывается сжатие (растяжение), тем сильнее деформируется образец.
Значение каждого материала находится между абсолютной и классической упругостью. То есть если изменения обратимы, после того как сила перестала действовать (форма стала прежняя – пример, сжатие пружины), то такие параметры нельзя называть пропорциональными.
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела — сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k — коэффициент жесткости:
k = EF/l (318.2.3)
где l — длина образца, F — площадь сечения, Е — модуль Юнга.
Как определяют свойства металлов
Проверяют не только то, что называют пределом прочности, но и остальные характеристики стали, например, твердость. Испытания проводят следующим образом: в образец вдавливают шарик или конус из алмаза – наиболее прочной породы. Чем крепче материал, тем меньше след остается. Более глубокие, с широким диаметром отпечатки остаются на мягких сплавах. Еще один опыт – на удар. Воздействие оказывается только после заранее сделанного надреза на заготовке. То есть разрушение проверяется для наиболее уязвимого участка.
Диаграмма растяжения мягкой стали
Прямолинейный участок 1 диаграммы (деформации растут пропорционально напряжениям о) переходит в кривую (небольшой отрезок между участками 1 и 2), т. е. деформации растут быстрее увеличения нагрузки, а от начальной точки («критической точки») участка 2 деформации увеличиваются без увеличения нагрузки (материал «течет»).
При напряжениях, близких к временному сопротивлению σи, продольные и поперечные деформации концентрируются в наиболее слабом месте, и в образце образуется шейка. Площадь поперечного сечения в шейке интенсивно уменьшается, что приводит к увеличению напряжений в месте сужения. В связи с этим, несмотря на то что нагрузка на образец снижается, в месте образования шейки нарушаются силы межатомного сцепления и происходит разрыв.
Напряжения (рис. выше) получают путем деления нагрузки на первоначальную площадь сечения. Истинная диаграмма растяжения (при напряжениях с учетом уменьшения площади сечения) не имеет нисходящей части.
При проведении опытов на растяжение площадь поперечного сечения стержней периодического профиля с необработанной поверхностью можно определить по формуле
где G — вес образца стержня периодического профиля, Н; L —длина образца, см.
Площадка текучести свойственна сталям с содержанием углерода 0,1-0,3%. При меньшем значении углерода перлитовых включений мало, отчего отсутствует сдерживающее влияние на развитие сдвигов в зернах феррита.
В высокопрочных сталях при большом числе включений развитие сдвигов полностью блокируется и явно выраженная площадка текучести отсутствует, т. е. материал не имеет физического предела текучести, необходимо определить величину условного предела текучести как напряжения, соответствующего остаточному удлинению Δε0,2 = 0,2% ε, где ε — удлинение образца.
Условный предел текучести для такой стержневой арматуры σ0,2 устанавливается по остаточному удлинению, равному 0,2%, и должен составлять не менее 80% браковочного значения предела прочности для каждого вида арматуры (рис. ниже). Откладывая величину Δε0,2 в соответствующем масштабе на оси абсцисс диаграммы растяжения, проводим наклонную линию ВС параллельно ОА до пересечения с кривой растяжения. Точка В определяет нагрузку σ0,2, соответствующую условному пределу текучести.
Механические свойства
Различают 5 характеристик:
- Предел прочности стали при растяжении и на разрыв это – временное сопротивление внешним силам, напряжение, возникающее внутри.
- Пластичность – это возможность деформироваться, менять форму, но сохранять внутреннюю структуру.
- Твердость – готовность встретиться с более твердым материалом и не получить значительных ущербов.
- Ударная вязкость – способность сопротивляться ударам.
- Усталость – длительность сохранения качеств под воздействием цикличных нагрузок.
Арматурная сталь
Основными показателями свойств арматурной стали являются:
- Предел текучести (физический) σу, МПа.
- Для сталей, не имеющих физического предела текучести, определяется предел текучести (условный) σ0,2, МПа — напряжение, при котором остаточное удлинение достигает 0,2% от длины участка образца. Определяют его тогда, когда при растяжении образца не обнаруживается ярко выраженного предела текучести (твердые стали).
- Временное сопротивление (предел прочности) σи, МПа.
- Относительное удлинение после разрыва ε — процентное отношение длины образца после разрыва к его первоначальной длине.
Проводя испытание образца, нагрузку на него увеличивают постепенно, ступенями. Начальную ступень нагружения следует принимать 5-10% от ожидаемой максимальной нагрузки. Каждая ступень должна составлять не более 20% от нормативной нагрузки. В конце каждой ступени увеличение нагрузки на образец приостанавливают. Под действием этой нагрузки образец находится не менее 10 мин. Доведя нагрузку до нормативного значения, образец выдерживается 30 мин. Эти выдержки необходимы для выяснения закономерности приращения перемещений и деформаций.
После достижения нагрузкой полуторной величины нормативного значения, дальнейшее увеличение ведут ступенями вдвое меньшими, давая после каждой ступени выдержку не менее 15 мин. Такой порядок дает возможность более точно установить величину предельной (разрушающей) нагрузки.
Деформации рекомендуется замерять приборами до достижения нагрузкой величины не более чем 1,25 от нормативной величины. После этого приборы снимаются. Это делается с целью избежания порчи приборов.
Начальная расчетная длина цилиндрических образцов из необработанной арматурной стали назначается равной десяти начальным (до испытания) диаметрам арматурного стержня.
Измерение начальной и конечной (длина расчетной части после разрыва образца) расчетных длин, а также диаметра необработанного образца производится с точностью 0,1 мм. До появления деформации образца перемещение подвижного захвата происходит без нарастания или с небольшим увеличением нагрузки, которая необходима для устранения зазора как в механизме машины, так и между образцами и захватами. Поэтому на диаграмме в самом начале испытания появляется сначала горизонтальный, а затем криволинейный участок. При начальной нагрузке, составляющей 10% от разрывного усилия, на образец наносят две риски. Расстояние между рисками является начальной расчетной длиной образца.
В продолжение всего испытания ведется наблюдение за поведением образца по диаграмме, вычерчиваемой записывающим прибором разрывной машины.
По оси ординат диаграммы откладываются напряжения σ, а по оси абсцисс относительные деформации образца ε, представляющие отношение удлинения образца к его первоначальной длине (рис. ниже). Криволинейный участок в начале диаграммы рассматривать не следует, поэтому продолжаем прямолинейный отрезок диаграммы до оси абсцисс и получаем точку О — начало диаграммы.
На диаграмме (рис. ниже) можно выделить три участка работы стали: 1 — участок упругой работы; 2 — участок пластической работы; 3 — участок упруго-пластической работы. В большинстве простейших расчетов считается, что сталь работает в пределах первого участка упруго, т. е. напряжения в элементах ограничиваются пределом текучести — σу. Соответственно, нормативные и расчетные сопротивления, необходимые для расчета конструкций, принимаются по пределу текучести.
Классы прочности и их обозначения
Все категории записаны в нормативных документах – ГОСТах, по ним все российские предприниматели изготавливают любой металлопрокат и прочие металлические изделия. Вот соответствие обозначения и параметра в таблице:
| Класс | Временное сопротивление, Н/мм2 |
| 265 | 430 |
| 295 | 430 |
| 315 | 450 |
| 325 | 450 |
| 345 | 490 |
| 355 | 490 |
| 375 | 510 |
| 390 | 510 |
| 440 | 590 |
Видим, что для некоторых классов остается одинаковыми показатели ПП, это объясняется тем, что при равных значениях у них может различаться текучесть или относительное удлинение. В зависимости от этого возможна различная максимальная толщина металлопроката.
Модули упругости
Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).
Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности
Модуль Юнга также определяется опытным путем при испытании стандартных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:
σ = Р/Fо (318.3.1), (317.2)
а относительное удлинение ε — отношению абсолютной деформации к начальной длине
εпр = Δl/lo (318.3.2)
то модуль Юнга согласно закону Гука можно выразить так
Е = σ/εпр = Plo/FoΔl = tgα (318.3.3)
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов
Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным
Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:
εпоп = Δd/do (318.3.4)
Тогда коэффициент Пуассона можно выразить следующим уравнением:
μ = εпоп/εпр (318.3.5)
Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига
Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.
При угловых деформациях рассматриваемое сечение перемещается не линейно, а под некоторым углом — углом сдвига γ к начальному сечению. Так как касательные напряжения равны силе, деленной на площадь в плоскости которой действует сила:
т = Р/F (318.3.6)
а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:
tgγ = Δl/h (318.3.7)
то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:
G = т/γ = Ph/FΔl (318.3.8)
Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:
Е = 2(1 + μ)G (318.3.9)
Значения постоянных Е, G и µ приводятся в таблице 318.1
Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов
Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.
Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:
Предел упругости Ру
Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:
σу = Ру/Fo (318.2.4)
Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ0.001, σ0.01 и т.д.
Предел текучести Рт
σт = Рт/Fo (318.2.5)
Ограничивает участок диаграммы на котором деформация увеличивается без значительного увеличения нагрузки (состояние текучести). При этом по всему объему образца происходит частичный разрыв внутренних связей, что и проводит к значительным пластическим деформациям. Материал образца полностью не разрушается, но его начальные геометрические размеры претерпевают необратимые изменения. На отшлифованной поверхности образцов наблюдаются фигуры текучести — линии сдвигов (открытые профессором В. Д. Черновым). Для различных металлов углы наклона этих линий различны, но находятся в пределах 40-50о. При этом часть накопленной потенциальной энергии необратимо расходуется на частичный разрыв внутренних связей. При испытании на растяжение принято различать верхний и нижний пределы текучести — соответственно наибольшее и наименьшее из напряжений, при которых возрастает пластическая (остаточная) деформация при почти постоянной величине действующей нагрузки.
На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.
Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.
Предел прочности Рмакс (временное сопротивление)
Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:
σв = Рмакс/Fo (318.2.6)
После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Рмакс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.
Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.
В таблицах 318.2 — 318.5 приведены ориентировочные величины пределов прочности для некоторых материалов:
Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.
Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.
Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс
Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон
Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород
Разрушение материала Рр
Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования «шейки» значительно изменяется площадь сечения образца в районе «шейки». Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:
Рисунок 318.3. Диаграмма напряжений: 2 — по отношению к начальной площади поперечного сечения, 1 — по отношению к изменяющейся площади сечения в районе шейки.
Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.
Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:
ψ = 100(Fo — F)/Fo (318.2.7)
где Fo — начальная площадь поперечного сечения образца (площадь поперечного сечения до деформации), F — площадь поперечного сечения в районе «шейки». Чем больше значение ψ, тем более ярко выражены пластические свойства материала. Чем меньше значение ψ, тем больше хрупкость материала.
Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.
За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:
Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)
Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.
Формула удельной прочности
R с индексом «у» – обозначение данного параметра в физике. Рассчитывается как ПП (в записи – R) поделенное на плотность – d. То есть этот расчет имеет практическую ценность и учитывает теоретические знания о свойствах стали для применения в жизни. Инженеры могут сказать, как меняется временное сопротивление в зависимости от массы, объема изделия. Логично, что чем тоньше лист, тем легче его деформировать.
Формула выглядит так:
Ry = R/d
Здесь будет логичным объяснить, в чем измеряется удельный предел прочности. В Н/мм2 – это вытекает из предложенного алгоритма вычисления.
Диаграмма растяжения стали, не имеющей площадки текучести
За площадкой текучести кривая (рис. выше) опять идет вверх, нагрузка снова начинает расти и в самой верхней точке достигает своего наибольшего значения (σмакс — разрушающая нагрузка), после чего вновь уменьшается до момента разрыва образца.
Относительное удлинение вычисляется по формуле
где Lk — длина образца после разрыва (конечная длина), мм; L — расчетная начальная длина образца, мм.
Чтобы измерить длину образца после разрыва, обе его части складываются по длине и штангенциркулем измеряют расстояние между рисками, соответствующими принятой расчетной длине.
Помимо основных характеристик σy, σu, ε, определяемых по результатам испытаний на растяжение, важными показателями арматурных сталей являются отношения предела текучести к временному сопротивлению и предела пропорциональности к пределу текучести.
Отношение σy/σu характеризует резерв прочности стали. В арматурных сталях обычной и повышенной прочности это отношение близко к 0,6, что свидетельствует о достаточно большом резерве работы материала и позволяет использовать в широких пределах пластические свойства стали. Для высокопрочных арматурных сталей предел текучести близок к временному сопротивлению σ0,2/σu=О,8-0,9, что ограничивает использование работы материала в упругопластической стадии.
Модуль упругости арматурной стали Es. Так как арматурная сталь работает в упругопластических условиях, расчетные значения модуля деформации (упругости) ее принимают равными их нормативным значениям или в,зависимости от класса арматурной стали по таблице ниже.
Использование свойств металлов
Два важных показателя – пластичность и ПП – взаимосвязаны. Материалы с большим первым параметром намного медленнее разрушаются. Они хорошо меняют свою форму, подвергаются различным видам металлообработке, в том числе объемной штамповке – поэтому из листов делают элементы кузова автомобиля. При малой пластичности сплавы называют хрупкими. Они могут быть очень твердыми, но при этом плохо тянуться, изгибаться и деформироваться, например, титан.
Сопротивление
Есть два типа:
- Нормативное – прописано для каждого типа стали в ГОСТах.
- Расчетное – получается после вычислений в конкретном проекте.
Первый вариант скорее теоретический, для практических задач используется второй.
Пути увеличения прочностных характеристик
Есть несколько способов это сделать, два основных:
- добавка примесей;
- термообработка, например, закал.
Иногда они используются вместе.
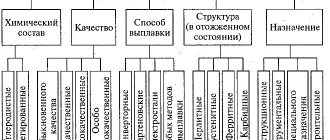
Общие сведения о сталях
Все они обладают химическими свойствами и механическими. Ниже подробнее поговорим о способах увеличения прочности, но для начала представим схему, на которой представлены все разновидности:
Также посмотрим более подробное видео:
Все они обладают химическими свойствами и механическими. Ниже подробнее поговорим о способах увеличения прочности, но для начала представим схему, на которой представлены все разновидности:
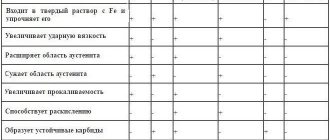
Углерод
Чем больше углеродность вещества, тем выше твердость и меньше пластичность. Но в составе не должно быть более 1% химического компонента, так как большее количество приводит к обратному эффекту.
Марганец
Очень полезная добавка, но при массовой доле не более двух процентов. Обычно Mn добавляют для улучшения качеств обрабатываемости. Материал становится более подвержен ковке и свариванию. Это объясняется вытеснением кислорода и серы.
Кремний
Эффективно повышает прочностные характеристики, при этом не затрагивая пластичность. Максимальное содержание – 0,6%, иногда достаточно и 0,1%. Хорошо сочетается с другими примесями, в совокупности можно увеличить устойчивость к коррозии.
Азот и кислород
Если они попадают в сплав, но ухудшают его характеристики, при изготовлении от них пытаются избавиться.
Легирующие добавки
Также можно встретить следующие примеси:
- Хром – увеличивает твёрдость.
- Молибден – защищает от ржавчины.
- Ванадий – для упругости.
- Никель – хорошо влияет на прокаливаемость, но может привести к хрупкости.
Эти и другие химические вещества должны применяться в строгих пропорциях в соответствии с формулами. В статье мы рассказали про предел прочности (кратковременное сопротивление) – что это, и как с ним работать. Также дали несколько таблиц, которым можно пользоваться при работе. В качестве завершения, давайте посмотрим видеоролик:
Чтобы уточнить интересующую вас информацию, свяжитесь с нашими менеджерами по телефонам;; 8 (800) 707-53-38. Они ответят на все ваши вопросы.