Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки для заданной системы изгибающих нагрузок.
Задача
Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a
=0,8 м,
l
=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=
l
/400
Рис. 1
Другие примеры решений > Помощь с решением задач >
Решение
Построение эпюр Q и М
Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки
Внутренние силовые факторы Qy и Mx в пролете балки 0 ≤ z2 ≤ l
QII= — RB+ qz2= -52+30∙z2 QII(z=0)= -52 кН QII(z=l)= -52+30∙4=68 кН
MII=RB∙z2-qz22/2=52z2-30∙z22/2 MII (z=0)= 0 MII (z=l)= -32 кНм
На консоли l ≤ z1≤ (l+a)
QI= — RB+ ql — RA=-52+30∙4-108=-40 кН
MI=RB z1-ql(z1-l/2)+RA(z1-l)=52z1-30∙4(z1-4/2)+108(z1-4) MI (z=l)= -32 кНм MI (z=l+a)= 0
По этим данным построены эпюры Q и М.
Условие прочности для двутавра
Так вот, условие прочности, при плоском изгибе, будет выглядеть так:
В неравенстве слева, записано максимальное расчетное напряжение, а справа напряжение допустимое.
Максимальное расчетное напряжение, в сопромате, находят двумя способами:
Как отношение максимального изгибающего момента к моменту сопротивления:
Либо по такой формуле:
Где М — максимальный изгибающий момент, y — расстояние от нейтральной линии до крайней точки сечения, J — момент инерции сечения.
Момент инерции и момент сопротивления связаны следующей связью:
Подбор сечения двутавровой балки
Так как Мmах = 45 кНм, то
Wx≥Mmax / [σ] = 45∙103 / 160∙106= 0,281 м3= 281 см3
.
О том, как подбирается сечение балки
По сортаменту выбираем двутавр № 24, для которого Wx = 289 см3, Ix= 3460 см4, Smax = 163 см3, h = 24 см, bп = 11,5 см, t = 0,95 см, d = bc = 0,56 см, h0 = h-2t = 22,1 см.
Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.
σmax = Mmax / Wx = 45∙103 / 289∙10-6= 156∙106 Па = 156 МПа
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:
- Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:
- Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:
- Все сосредоточенные моменты нужно умножать дробь:
\[ M\cdot \frac { { x }^{ 2 } }{ 2 } \]
- Все сосредоточенные силы нужно умножать дробь:
\[ F\cdot \frac { { x }^{ 3 } }{ 6 } \]
- Начало и конец распределенных нагрузок нужно умножать на дробь:
\[ q\cdot \frac { { x }^{ 4 } }{ 24 } \]
Откуда такие цифры и степени взялись? Все эти вещи вытекают при интегрировании дифференциального уравнения упругой линии балки, в методе начальных параметров все эти выводы опускаются, то есть он является как бы упрощенным и универсальным методом.
Формулы прогибов
С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } \]
В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.
Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:
\[ E{ I }_{ z }{ V }_{ B }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 8+\frac { { R }_{ A }\cdot { 8 }^{ 3 } }{ 6 } -\frac { F\cdot { 8 }^{ 3 } }{ 6 } -\frac { q\cdot 6^{ 4 } }{ 24 } +\frac { q\cdot 2^{ 4 } }{ 24 } =0 \]
Упрощаем уравнение:
\[ E{ I }_{ z }{ \theta }_{ A }\cdot 8+874.67=0 \]
Выражаем угол поворота:
\[ { \theta }_{ A }=-\frac { 874.67 }{ 8E{ I }_{ z } } =-\frac { 109.33кН{ м }^{ 2 } }{ E{ I }_{ z } } \]
Подставляем это значение в наше первое уравнение и находим искомое перемещение:
\[ E{ I }_{ z }{ V }_{ C }=\frac { -109.33\cdot 4E{ I }_{ z } }{ E{ I }_{ z } } +\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } =-\frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } \]
Проверка сечения балки по касательным напряжениям
Так как Qmax = 68 кН, то
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:
Построение эпюры нормальных напряжений
Построение эпюры касательных напряжений
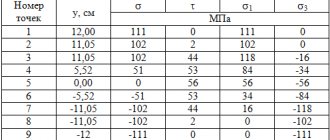
В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:
М = -32 кНм и Q = 68 кН.
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1
Таблица 1
Результаты расчета в примере
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Калькулятор
| Пример расчета |
Калькуляторы по теме:
- Сбор нагрузок на балки перекрытия онлайн
- Расчет прямоугольной трубы
- Расчет квадратной трубы
- Расчет швеллера
- Расчет уголка
- Расчет деревянной балки
- Расчет двутавра на устойчивость.
Разновидности балок, применяемых в строительстве
Современная стройиндустрия при возведении сооружений промышленного и жилого назначения, практикует использование стержневых систем различного сечения, формы и длины, изготовленных из различных материалов.
Наиболее большее распространение получили стальные и деревянные изделия. В зависимости от используемого материала, определение значения прогиба имеет свои нюансы, связанные со структурой и однородностью материала.
Деревянные
Современное малоэтажное строительство индивидуальных домов и загородных коттеджей практикует широкое использование лаг, изготовленных из хвойных и твердых пород древесины.
В основном, деревянные изделия, работающие на изгиб, применяются для обустройства напольных и потолочных перекрытий. Именно эти элементы конструкции испытают наибольшее действие поперечных нагрузок, взывающих наибольший прогиб.
Стрела прогиба деревянной лаги зависит:
- От материала (породы древесины), который использовался при изготовлении балки.
- От геометрических характеристик и формы попечённого сечения расчетного объекта.
- От совокупного действия различного вида нагрузок.
Критерий допустимости прогиба балки учитывает два фактора:
- Соответствие реального прогиба предельно допустимым значениям.
- Возможность эксплуатации конструкции при наличии расчетного прогиба.
Стальные
Имеют более сложное сечение, которое может быть составным, выполненным из нескольких видов металлического проката. При расчете металлоконструкций, помимо определения жесткости самого объекта его элементов, часто появляется необходимость определения прочностных характеристик соединений.
Обычно, соединение отдельных элементов стальной металлоконструкции проводится:
- С использованием электросварки.
- Путем применения резьбовых (шпилечных, болтовых и винтовых) соединений.
- Соединением заклепками.
Примеры расчетного сопротивления
Для расчета двутавровой балки может потребоваться такая величина, как расчетное сопротивление (Ry). Она зависит от марки стали, из которой произведена балка. Например, приведены готовые величины:
- С 235 – 230 МПа;
- С 345 – 335 МПа;
- С 255 – 250 МПа.
Модуль упругости берут одной величиной, равной для стали: Е = 200 000 МПа. Расчет нагрузки двутавровой балки осуществляется на основе вычислений несущей способности. К этой цифре прибавляют 30% на прочность (это относится лишь к сварным профилям).
Чем заменить вычисление прогиба?
При возведении небольшого дома в частном строительстве не обязательно находить все величины для сложных расчетов. Некоторые параметры могут совсем не влиять на качество строительства. Например, для небольшого домика, дачи определяют одну величину из двух:
- Прогиб двутавровой балки;
- Несущая способность.
При этом прогиб в частном строительстве рассчитывать не обязательно. Однако его величина используется при выборе отделки для потолка, так как тяжелые материалы при неблагоприятных условиях лучше не применять.